Neo Pascal的语法分析器是基于自上而下的语法分析法构造的，所以本书以详细介绍自上而下的语法分析器相关理论及其构造为主。自上而下的语法分析器短小精悍，适于手工构造。而自下而上的语法分析器的分析表非常复杂，几乎不可能手工完成。许多经典编译器偏向于手工编码完成，故自上而下的语法分析器成为不少经典编译器的不二之选。构造自上而下的语法分析器主要包括三项工作：

1)变换程序设计语言的文法，使之满足自上而下的语法分析法的要求。

2)构造文法的First集合与Follow集合，作为分析算法选择候选式的依据。

3)编码实现自上而下的语法分析算法。

1．LL(1)文法

自上而下的语法分析法适用于大多数程序设计语言，但确实也有一些特殊的文法不适用于自上而下的语法分析法。如果给定文法符合如下两个条件（读者先不必深究）：

(1)文法不含左递归。

(2)对于文法中每一个非终结符A的各个候选式的First集合、Follow集合两两不相交。即若

A→α₁|α₂|…|α_n

则

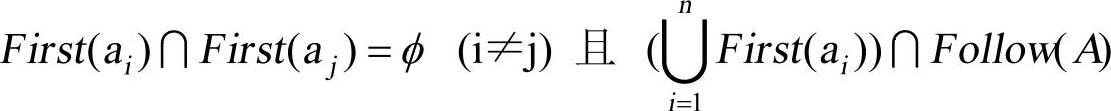
则称为LL(1)文法。笔者先解释一下LL(1)的含义，第一个“L”是scanning from left to right的意思，即自左向右扫描输入单词。第二个“L”是leftmost derivation的意思，即最左推导。而“(1)”表示超前搜索一个单词。

前面，已经讨论了如何将一个普通的文法变换为LL(1)文法。不过，并不是任何文法都可以变换为LL(1)文法的。通过任何方法都无法使其满足上述两个条件的文法就是真正的非LL(1)，也就不适用于LL(1)语法分析法了。当然，LL(1)文法也是存在不足之处的。读者不难发现，经过变换后的LL(1)文法的可读性、可理解性远不及原始文法，这也是自上而下的语法分析法的最大缺点。

2．First集合

下面，笔者将给出First集合的定义。

如果A是任意的文法符号串，则将从A推导出的串的开始符号的终结符集合称为First（A），即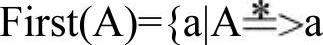…，a是终结符}。如果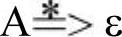，则ε也属于First（A）。

当候选式不为空字时，First集合是语法分析器选择候选式的重要依据。如果当前需被替换的非终结符为A，而超前搜索得到的输入单词T属于First（A→B）集合，则选择候选式B替代非终结符A。这里，主要讨论如何计算LL（1）文法的First集合。

对于任意文法符号A，可以应用下列规则计算First（A）：

1）如果A是终结符，则First（A）就是{A}。

2）如果A→ε是一个候选式，则将ε加入First（X）中。

3）如果A是非终结符，且A→Y₁Y₂…Y_n是一个产生式，则

a）First（Y₁）中的所有符号加入First（A）中。

b）如果对于某个i而言，a∈First（Y_i）并且ε∈First（Y₁），…，First（Y_i-1），即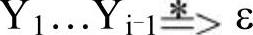，则将a加入First(A)中。

c)若对于所有的j=l，2.…．，k，ε属于First(Y_i)，则将ε加入First(X)中。

4)重复以上过程，直到没有终结符或ε可加到某个First集合为止，即迭代过程结束。

3．Follow集合

前面已经介绍了Follow集合的作用。在正式给出Follow集合的定义之前，不妨先思考一个问题。读者应该还记得在设计词法分析器时，为了便于词法分析器超前搜索算法的实现，统一在整个源程序文本的尾部自动添加了一个空格字符。这样，词法分析器就可以运用超前搜索算法顺利识别源程序文本的最后一个单词。那么，在设计语法分析器时会不会存在相同的问题呢？的确如此，设计语法分析器时需要定义一个特殊的结束单词以表示源程序终结，一般可以称为文法结束符，记作“$”（有些书上记作“≠}”）。一门程序设计语言的文法结束符是由语言设计者定义的，文法结束符有时可以在文法中体现，例如，Pascal中规定“．”就是文法结束符。文法结束符有时并不是显式存在的，例如，C、BASIC、Java等并没有明确定义文法结束符，这就需要编译器设计者在设计语法分析器时隐式定义。文法结束符是一个终结符，它保证了超前搜索算法的一致性。由于Neo Pascal显式定义了结束符，因此，并不需要考虑隐式定义的相关技巧。

如果A是一个非终结符，则Follow(A)是包含所有在句型中紧跟在A后面的终结符a的集合，即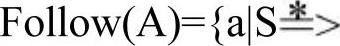…Aa…，a是终结符}。如果…A，则$∈Follow（A）。实际上，Follow(X)表示非终结符X后紧接着可以出现的终结符或文法终结符的集合。当候选式为e时，Follow集合是语法分析器选择候选式的重要依据。如果当前需被替换的非终结符为A，而超前搜索得到的输入单词T属于Follow(A)集合且不属于任何First(A)集合时，则选择e候选式进行推导。

对于文法符号A，可以应用下列规则计算Follow(A):

1)如果A是文法开始符，则将$置于Follow(A)中。其中，$表示文法的结束符。

2)若存在产生式A—aBb，则将First(b)中除了ε以外的符号都放入Follow(B)中。

3)若存在产生式A—aB，或者A—aBb，其中First(b)中包含ε（即b兰>ε），则将Follow(A)中的所有符号都放入Follow(B)中。

4)重复以上过程，直到没有终结符或ε可加到某个Follow集合为止，即迭代过程结束。

例3-10 计算文法3-10的First集合与Follow集合。见表3-1。

表3-1 文法3-10的First集合与Follow集合

计算First集合：

为了便于计算，首先计算右部首符号为终结符的产生式的First集合。由于首符号为终结符的产生式的First集合就是本身，所以，First(op2→／)={／）、First(op2→*)={*）、First(opl→+)={+）、First(opl→-)={-）、First(I→var)= {var}、First(I→const)= {const}、First(F→-F)={-}、First(F→(E))={(}。(www.daowen.com)

然后，计算右部首符号为非终结符的产生式的First集合。例如，First(F→I)={var,const}，因为I是非终结符，First(F→I)是I的所有产生式的First集合的并集。同理，可以计算得到其他右部首符号为非终结符的产生式的First集合。

最后，右部为ε候选式的First集合不存在的，则无需计算。

计算Follow集合：

理论上讲，每个非终结符都有一个且只有一个Follow集合。不过，由于Follow集合仅可用于选择ε候选式，因此，只需计算存在ε候选式的非终结符的Follow集合。这里，只需要计算El和Tl的Follow集合即可。另外，计算非终结符的Follow集合时，经常用到文法开始符的Follow集合，为了方便计算，文法开始符的Follow集合也需要事先计算。

首先计算文法开始符E的Follow集合。由于E是文法开始符，故先将文法结束符$加入Follow(E)。同时，非终结符E也出现在产生式7的右部符号串中，不难发现，产生式7的右部符号串中紧接着E后的是终结符“）”，根据计算规则2，终结符“）”也被加入Follow(E)。计算得到Follow(E)={$，)}。

下面，计算El的Follow集合。非终结符El出现在产生式1、2的右部符号串中。由于产生式2的左部是El本身，不需要处理，那么，只需考虑产生式1。不难发现，产生式1的形式与计算规则3描述的产生式形式类似，根据计算规则3，必须将Follow(E)集合添加到Follow(El)中。所以，Follow(El)=Follow(E)={$,)}.

最后，计算Tl的Follow集合。非终结符Tl出现在产生式4、5的右部符号串中。由于产生式5的左部是Tl本身，不需要处理，那么，只需考虑产生式4。产生式4的形式与计算规则3描述的产生式形式类似，根据计算规则3，必须将Follow(T)集合添加到Follow(Tl)中，故必须先计算Follow(T)集合。非终结符T出现在产生式1、2的右部符号串中，而紧接着T后的非终结符都是El。根据计算规则2，先将First(El)集合（除了ε外）添加到Follow(T)中，此时，Follow(T)={+，一}。同时，由于El存在空字候选式，故必须将Follow(El)添加到Follow(T)中。这样就得到了Follow(Tl)=Follow(T)={+，一，$，）}。

计算结果见表3-1。

4．LL(1)语法分析器

至此，已经完成了构造语法分析器的准备工作，主要包括变换LL(1)文法、计算First集合及Follow集合等。当然，运用类似于例3-7的方法借助于文法的First集合与Follow集合完全可以构造递归下降分析器。递归下降分析器非常有利于手工构造语法分析器，它使语法分析器短小精悍、灵活多变。但递归下降分析器存在两个缺点：

(1)算法本身过多依赖程序设计语言文法。

(2)该算法必须有实现递归的程序设计语言编译器的支持。

虽然大多数通用机的编译器都支持递归调用，但不支持递归调用的情况并不少见。不支持递归调用的原因很多，大部分是由于程序设计语言或者编译器设计本身的问题，例如，早期的Fortran就是由于编译器采用了静态存储分配方式，从而无法实现递归调用。但是，有时也可能是由于计算机硬件系统没有系统栈结构而不支持递归调用的。在第8章中将详细讨论系统栈的问题。

在数据结构中，许多算法都有递归与非递归两种描述形式，有些数据结构教材甚至还讲述了如何将递归算法改写为非递归算法。同样，也可以将递归下降分析器改写成非递归的自上而下的语法分析器。递归算法的本质就是利用系统栈暂存函数的运行时环境（如局部变量、返回地址、参数等），而系统栈对于递归程序本身是透明的，用户在编写递归程序时并不需要考虑系统栈的管理。如果试图摒弃递归描述形式，就必须定义一种数据结构来模拟系统栈，栈结构当然就是不二之选了。

LL(1)语法分析器有一个输入缓冲区、一个分析栈、一张分析表和一个输出流。通常，输入缓冲区就是词法分析器的输出单词流，输出流主要用于输出语法分析过程中的出错信息。分析表是一张依据文法First、Follow集合构造的二维表，它是LL(1)语法分析器的核心。而分析栈是一个用户定义的栈结构，栈的元素是文法的符号，既可以是终结符也可以是非终结符。

LL(1)语法分析器如图3-6所示，由一个主控程序控制，主控程序根据分析栈栈顶元素S（符号）和输入缓冲区的当前单词符号a决定语法分析器的下一步动作：

1)如果S=a_$，则语法分析成功完成。

2)如果S=a≠$，则语法分析器弹出分析栈栈顶符号E，并将输入缓冲区的指针后移一个符号。

3)如果S是非终结符，则查询分析表T的T[S，a]项。分析表T中的项只有两种值，即S的某个候选式或出错标志。如果T[S，a]项是非终结符S的某个候选式，则先弹出分析栈栈顶符号S，再将T[S，a]项的候选式右部符号串反序入栈（如果候选式右部符号为e，则不需要入栈）。如果T[S，a]项是出错标志，则表示输入源程序不正确，语法分析器调用错误处理程序或提示出错信息。

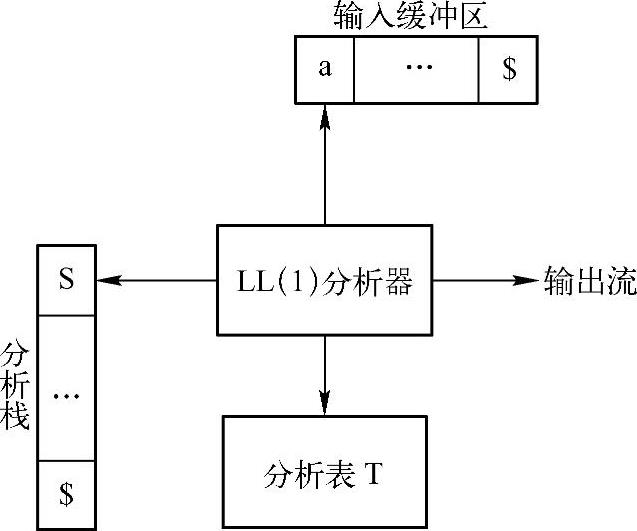
图3-6 LL（1）语法分析器模型

4）如果S是终结符，但S≠a，则表示输入源程序不正确，语法分析器调用错误处理程序或提示出错信息。

下面就来看看LL（1）语法分析器的伪代码实现。

程序3-2LL（1）语法分析器的伪代码实现

这里只给出了算法的伪代码，在后文剖析Neo Pascal语法分析器源代码时，将详细给出预测分析器的C++源代码。

仔细分析LL(1)语法分析器的算法，应该不难理解分析表的功能。分析表的作用是：当非终结符S遇到输入符号a时，辅助语法分析器选择哪条候选式进一步推导。如果无法选择合适的候选式推导，则表示输入源程序不正确。所以，分析表的表项只有两种情况，即候选式或出错标志。

前面已经介绍了递归下降分析器选择候选式的依据是文法的First、Follow集合。在构造分析表时，同样也不少了它们的帮助。下面通过实例讲解如何构造分析表。

例3-11 根据文法3-10构造预测分析表，见表3-2。

表3-2 预测分析表

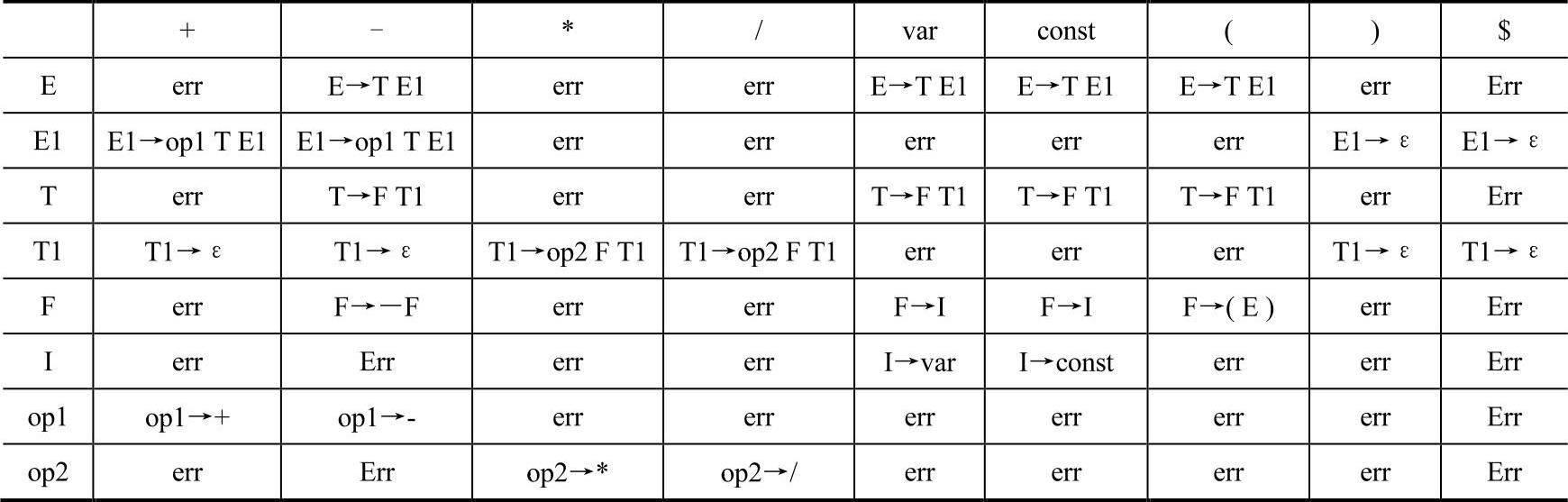
首先，以非终结符为行，终结符为列，构造一张空表。

然后，依次处理文法中每个产生式，以左部非终结符定位行，以产生式的First集合中的终结符定位列，将该产生式填入相应单元格中。以产生式E→T El为例，已经计算得到该产生式的First集合为{f’一，var,const}。首先，定位到非终结符E所在的行，然后，将产生式分别填入E行的“（”、“”、“var”、“const”列。对于ε产生式（例如Tl→ε），则以Follow集合中的终结符定位列，将产生式填入相应单元格中。

最后，在所有空单元格中，填入“err'’，表示“出错标志”。

至此，从语法分析器设计的角度重新审视先前提到的LL(1)文法的两个条件，就不难理解其用意了。条件1规定LL(1)文法必定不含左递归，关于这个条件，笔者已经详细分析了左递归文法为什么会使语法分析器失效。而条件2规定LL(1)文法的任意一个非终结符的各个候选式的First集合及其Follow集合两两不相交，从构造分析表的过程分析就不难理解此条件的必然性了。如果文法中某一个非终结符的各个候选式的First集合及其Follow集合存在交集，那么，在构造分析表时，必定会有冲突（即一个单元格中填入多个产生式的情况）。显然，语法分析器就无法依据分析表选择适合的候选式，这是语法分析器无法接受的。

综上所述，笔者已经详细阐述了LL(1)语法分析法的相关理论与技术，这是剖析Neo Pascal语法分析器源代码的基础。LL(1)语法分析法并不是唯一的语法分析方法，但是，它比其他语法分析法更适合于手工构造。对于一门实际的程序设计语言而言，计算First、Follow集合及构造预测分析表有时可能比较烦琐，但是与自下而上语法分析法的分析表相比还是简单的。当然，任何事物都存在两面性，LL(1)语法分析法也存在一定不足之处，就是文法的限制较多。且不论是否任何程序设计语言的文法都可以等价地消除左递归，即使是消除了左递归的文法也已经面目全非，可读性远不及原始的文法了。相比之下，自下而上语法分析法对文法的限制远小于自上而下语法分析法。在某些情形下，自下而上语法分析法也可以实现非常优美的语法分析器。LR分析法是最著名的自下而上语法分析法，除了不适用于手工编码实现分析器外，它可以说是一种近乎完美的语法分析法。关于LR的更多内容，不再赘述，读者可以参考编译原理教材。