自上而下的语法分析法的核心思想就是模拟最左推导方式设计语法分析器。为什么是最左推导呢？这个问题非常简单，参考了例3-4后就不难发现，如果使用最右推导构造语法分析法，终结符的匹配将从输入单词流的最末端开始，这样的处理对于处理符号表、语义分析都是非常困难的。实际上，读者可以想象，如果逆向阅读源程序的话，对于理解程序是非常不便的。同样，再比较例j-j的最左推导，实际上就是模拟正向阅读源程序的过程，这种方式将便于语义分析等。这就是为什么自上而下的语法分析法都是模拟最左推导的原因。

在讲述文法推导时，笔者提到了推导过程中有两个选择，即选择哪个非终结符被替换及如何选择合适的候选式替换该非终结符。前面，只是凭直觉试探地选择候选式替换非终结符，并没有从算法上讨论这个问题。针对这个问题，熟悉算法设计的读者最先想到的一种解决办法就是回溯法。暂且不论回溯法的反复试探会大大降低语法分析的效率，回溯法本身就无法解决这个问题。通常，回溯法是在有限的集合中反复试探，当然，有时集合的数量级可能会很大。对有限语言的文法，在不考虑效率的情况下，回溯法或许是可行的。但是，程序设计语言的文法通常表示的句子集合是无限的，回溯法将无法试探穷举所有的可能句子，因此，使用回溯法就存在一定问题。下面，将详细讨论如何设计一个算法来解决这个问题。

例3-8 简单语法分析算法的设计。

【文法3-5】

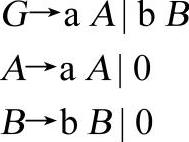
这个文法非常简单，对于任意输入单词流，程序3-1就是基于文法3-5的分析算法。

程序3-1

程序3-1的实现不算太复杂，对于有递归程序设计经验的读者来说只是小菜一碟。不过，读者可能会对程序3-1的算法实现提出疑问：文法3-5所描述的语言是一个非常简单的体系，似乎根本不需要使用如此复杂的递归算法实现其分析功能。就文法3-5本身而言，使用此算法实现的确有杀鸡用牛刀之感。但是，笔者给出此算法实现的目的并不在于简单实现文法3-5的语法分析，而旨在揭示一种通用的算法实现方式。实现上，这个算法实现是一种语法分析器的模型，读者仔细分析算法实现与文法形式，不难发现文法形式与算法实现的结构有惊人的相似之处。事实上，这种语法分析器就是将文法机械地变换为等价的算法实现。由于这种语法分析器中必定存在递归，故称之为递归下降分析器。大家不要小看这种语法分析器，许多经典编译器正是使用递归下降分析器实现的，著名的GCC、lcc就位列其中。递归下降分析器是自上而下语法分析器的鼻祖，本书讨论的语法分析器也是递归下降分析器的一种改进形式，称为LL(1)语法分析器。这里，笔者将从超前搜索一个单词的递归下降分析器着手，深入讨论语法分析器的构造。

显而易见，在例3-7中，可以通过超前搜索一个单词从而解决正确选择候选式的问题。那么，选择候选式的问题是不是真正解决了呢？事实并非如此，如果将文法3-5改写成文法3-6的形式，将无法构造类似程序3-1的递归下降分析器。

【文法3-6】

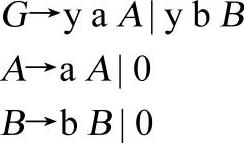
这是什么原因呢？比较以上两个文法，不难发现，因为G的两个候选式的首符号都是v，使用超前搜索一个单词无法作出正确选择。针对这种情况，是否必须改写分析算法呢？就此文法而言，确实可以通过改写分析算法使之超前搜索两个单词从而完成正确分析。但是，读者设想一下，由于文法产生式具有不确定性，如果G的两个候选式的首部有100个v，是否需要超前搜索100个单词呢？显然，修改分析算法的方案可行性较差。

换一个角度考虑，是否可以通过等价地改写文法解决这个问题？答案是肯定的。可以将文法改写成如文法3-7的形式，文法3-7与文法3-5的形式非常相似。当然，就可以构造出类似程序3-1的递归下降分析器，从而实现了文法3-7的语法分析功能。

【文法3-7】

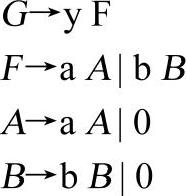
显然，通过增加一个非终结符及两个产生式就完成解决了此问题。这种处理方法与数学中提取公因子比较类似，通常称为提取公共左因子。通过前面两个文法的分析，不难发现，当文法的所有产生式右部首符号都是终结符时，就可以根据文法构造出类似程序3-1的递归下降分析器，从而完成语法分析的工作。但是，对于文法而言，这个条件似乎不太合理。请

参考文法3-8:

【文法3-8】

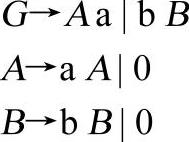
就文法形式而言（暂不考虑文法描述的语言），文法3-8与文法3-5、3-6、3-7的最大区别就是G的一个产生式的右部首符号不是终结符而是非终结符。这个变化对于分析算法就提出了挑战。如果依然使用原来的方法构造递归下降分析器，那么得到的分析器将出现死递归现象，这显然是不正确的。由于无法确定产生式G→Aa可以推导得到的第一个终结符，分析算法也就无法运用超前搜索一个输入单词的方法确定选择哪个产生式。读者应该不难想到，如果能够确定非终符A所能推导得到的所有句子的首终结符的集合，那么，就可以借助于这个集合确定何时该选择产生式G→Aa进行推导，通常将这个集合称为First集合。剩下的问题关键就在于如何确定First集合，这里就文法3-8进行讨论。在文法3-8中非终结符A可以推导得到的句子为“0”、“a0”、“aa0”……等等，不难看出非终结符A可以推导得到的所有句子的首符号的First集合就是[0，a]。由于程序设计语言的文法是预知的，可以依此方法事先求出每个产生式的First集合，而分析算法只需根据First集合选择候选式即可。

最后，再来讨论一种相对复杂的文法情况，请参考文法3-3。就文法形式特点而言，文法3-3与文法3-8似乎有点类似，它们都存在右部以非终结符为首的产生式。但是，读者可以尝试使用文法3-8的处理方法变换文法3-3，一定会发现即使求出产生式E→E opl T和T一Top2 F的First集合也没有任何意义。因为，产生式E→E oplT和产生式E一T的First集合必定是相同的，对于非终结符E而言，根据First集合选择候选式的算法将无法作出决策。如果同一个非终结符的候选式的First集合存在交集，即产生了分析冲突，表示该程序设计语言的文法不合适使用这种语法分析法。

如果诸如例3-3的标准表达式文法也不能分析，那么，本书讨论的语法分析法似乎已经失去了任何价值。显然，必须通过一些加工处理，使文法3-3满足语法分析方法的需求。

仔细分析产生式E→E opl T-定能够发现这个产生式的特点是产生式右部的第一个非终结符与产生式左部的非终结符相同，这种文法称为左递归文法。注意，读者必须考虑间接左递归文法的情况，例如：

【文法3-9】(www.daowen.com)

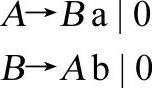
文法3-9表面上看并不是左递归文法，但将B→A b产生式的右部代入A→B a产生式的非终结符B时，即产生了左递归文法。左递归文法的最主要问题在于使用最左推导时，由于无法判定递归出口，将陷入死递归。

那么，左递归文法应该如何等价变换呢？必须明确指出：任何程序设计语言的文法必定存在递归（可以是左递归或者右递归）。因为没有递归的文法只能描述有限的语言（即语言的句子是可以枚举列出的），然而，任何程序设计语言必定是无限的语言。因此，不可能试图消除左递归文法的递归形式，只能将左递归形式等价变换为右递归形式或者其他形式，这种变换通常称为消除左递归。通常，使用如下公式将左递归文法等价变换为右递归文法：

右边是一个右递归文法。左右文法描述的语言是等价的，而右递归文法不存在左递归文法在最左推导时的不足之处。当然，消除左递归的变换也带来了一个新的问题，那就是e（空字）的出现。确实，这将给语法分析带来一定的不便，但并不像左递归文法那样存在不可逾越的障碍。

消除左递归的变换中，最重要的就是如何准确辨别给定产生式中哪一部分是公式中的a部分，而哪一部分是公式中的b部分。在实际文法中，a、b通常可能是符号串形式，而不是简单的单一符号。下面，通过实例说明如何辨别产生式的a、b部分。

例3-9 消除左递归变换。

注意：将单下画线部分看作a部分，将双下画线部分看作b部分。

经消除左递归后变成：

【文法3-10】

下面，再来看看右部为ε的候选式。当候选式右部为ε时，显然无法简单地求得此候选式的First集合。原因非常简单，源程序单词流中是不可能存在￡的，所以将ε加入First集合是无意义的。那么，何时选择ε候选式进一步推导呢？必须寻找一种有效的方法解决ε候选式的选择问题。

候选式的右部为ε即表示候选式的左部非终结符可以用ε替换。那么，候选式右部出现ε又意味着什么呢？先来看一个例子：

【文法3-11】

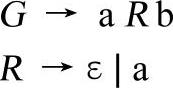
这个文法比较简单，它只包含两个句子，即ab和aab。显而易见，要推导出句子ab，符号串a R b中的非终结符R只能被ε替换。在符号串中某个非终结符被ε替换时，实际上就是将该非终结符从符号串中直接剔除。

理解了非终结符推导出ε的含义后，就可以继续讨论何时选择ε候选式了。图3-5是选择非终结符R的候选式时的指针状态示意图，指针1指向产生式符号串的R，而指针2由于超前搜索指向单词b。显然，候选式R—a的First集合是[a]，指针2指向的单词不在候选式的First集合内，故不能选该候选式。那么，唯有ε候选式可选，由于单词流ab是合法的句子，这里先假设选择ε候选式。这样，产生式符号串的非终结符R被直接剔除了，指针1就后移至符号b，并继续分析匹配。不难看出，当选择ε候选式时，实际上是非终结符R后的符号与单词流的当前符号比较。如果能事先分析得到非终结符R之后允许出现的符号串集合，便可求得此集合能推导出的所有句子的首终结符集合，记作Follow集合。那么，Follow集合就是选择R的ε候选式的依据。在文法3-11中，非终结符R后允许出现的符号串只有b，而由于b是终结符，所以它的Follow集合就是[b]。也就是说，在选择非终结符R的候选式时，当单词流中超前搜索得到的单词是b时，则选择R的ε候选式进行推导。由于一个非终结符的ε候选式最多只能有一条，故一个非终结符的Follow集合是唯一的。

图3-5 选择非终结符R的候选式时的指针状态示意图

至此，就可以借助于First集合与Follow集合辅助选择候选式了。在选择非终结符的候选式时，主要根据超前搜索得到的输入单词判定。当输入单词属于当前非终结符的某个候选式的First集合时，则选择该候选式进行推导。当输入单词属于当前非终结符的Follow集合时，则选择当前非终结符的ε候选式进行推导。必须注意两点：

（1）如果非终结符没有ε候选式，则它的Follow集合为空集。

（2）对于一个非终结符而言，它的全部First集合与Follow集合之间都是两两不相交的，否则说明文法不适用于超前搜索一个单词的语法分析法。

这里，引入了两个重要的集合：First集合与Follow集合，这是自上而下语法分析法的核心概念。目前，读者不必深究如何计算一些复杂文法的First集合与Follow集合，只需深入理解引入First集合、Follow集合的目的及其解决的问题，这远比后续学习如何计算重要得多。

综上所述，通过等价变换文法或少量修改分析算法等方式已经实现了一个语法分析器的简单原型。此原型目前还存在许多不足之处，将在后续章节中逐步完善。通过本小节学习，读者应该掌握根据文法的特点，提取公共左因子和消除左递归。另外，读者还学会了如何构造First集合、Follow集合来辅助选择候选式进行推导，它们是构造语法分析器的基础。