从图2-2中，不难发现，其中只有“搜索指针后移一个字符”一种处理动作（方框）。那么，读者不妨想象一下，词法分析器是否就只有这种处理动作呢？仔细分析手工识别单词的过程后，就可以发现事实确实如此。既然词法分析器的流程中条件判断（菱形框）比较复杂，而处理动作非常单一，因此，可以将普通流程图改造成一种专门用于描述条件判断的流程图。具体改造步骤如下：

1)把图2-2中所有上、下菱形（判断）之间的箭头用圆表示。

2)把图2-2中所有的菱形直接用箭头线表示，箭头上写上原菱形的判断成立与否的条件，即可得到图2-3。

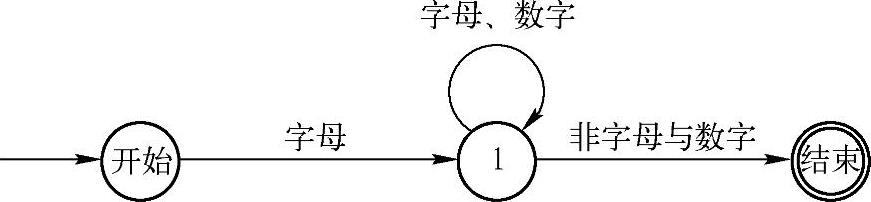
图2-3 识别Pascal标识符的状态转换图

这里省略了出错处理，由于词法分析器的出错处理可以统一完成，所以无需重复考虑。

那么，将图2-2改造成图2-3的意义是什么呢？实际上，主要针对词法分析器的流程特点，突出了流程中最为复杂的部分，省略或简化相对简单的部分，这样的改造便于更直观地分析问题的本质。这种分析问题的方法在软件系统分析与设计过程中较为常用，读者应该善于改进一些已有的工具，使之更有利于分析问题。

图2-3对于词法分析器设计具有非常重要的作用。在形式语言学中将这种图称为转换图(transition diagrams)，亦称为状态转换图。

转换图是一个有向图。在转换图中，圆表示状态，状态之间用箭弧连接。箭弧上的标记表示在箭弧始结点的状态下读入给定字符或字符集时，当前状态转到箭弧终结点所示状态。例如，图2-3在开始状态下，若输入字母，则转换到状态1。一张转换图只包含有限个状态（即有限个结点），其中，有一个是初始状态（图2-3中的“开始”状态），而且必须至少有一个终止状态（用双圈表示，读者可以将终止状态理解为可终止状态，而其他状态即为不可终止状态）。那么，如何运用转换图完成单词的识别呢？实际上，识别一个单词就是从初始状态经过数次转换到达终止状态的过程。如果某一个字符串的识别过程不能到达终止状态，说明输入字符串不能被该转换图接收。

下面，应用转换图来分析一个复杂的实例。在Pascal词法分析器中最复杂的就是识别实型常量的逻辑流程。Pascal的实型常量有两种形式：普通小数形式、科学记数法的小数形式，例如，2.34、23.4E32、46.1e-43、30.e12等都是合法的实型常量，而诸如.32、31。je、32.3E13.2等形式都是非法的实型常量。读者可以参考图2-4。(www.daowen.com)

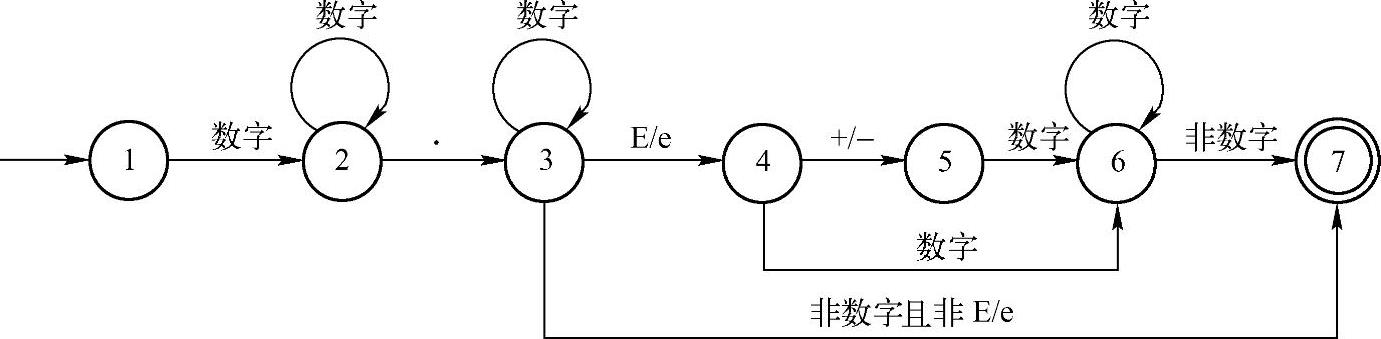
图2-4 识别Pascal实型常量的转换图

读者可能会有疑惑，为什么图2-4没有考虑实型常量的+／号？实际上，在词法分析时，只能将“”识别成运算符，但无法确定其到底是用作负号还是减号。这个工作将在语法分析阶段完成。因此，词法分析器无法确定是否将“”直接与后续常量组合。仅从识别实型常量的角度而言，图2-4已经足够完整了。但从实际编译器设计的角度而言，可能还需作少量改进。这里，值得注意的是标准Pascal中的数组声明形式，例如：

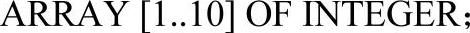
这种声明形式对图2-4提出了挑战。在上例中，当词法分析器读取第二个“．”时，将直接转到状态7，随即完成单词“1．”的识别，这与原始的语义是完全相悖的。实际上，正确的识别结果应该是得到“1”、“．．”、“10”三个单词。

下面，再来看看如何应用图2-4识别字符串“92.3E1”。这是一个合法的实数常量表示形式。首先，从开始箭头进入状态1。在状态1时，读取到数字即转入状态2。在状态2时，读取第二个字符“2”，根据圆弧箭头指示，状态2遇到数字时仍然停留在状态2。在状态2时，读取第三个字符“．”，状态2即转入状态3。在状态3时，读取第四个字符“3”，状态3遇到数字时仍然停留在状态3。在状态3时，读取第五个字符“E”，状态3即转入状态4。在状态4时，读取第六个字符“1”，状态4转换为状态6。根据超前搜索识别原则，词法分析器继续读取下一个字符，且下一个字符必定不是数字。在状态6时，读取一个非数字字符即转入状态7。至此，状态转换停留在状态7上，状态7是终止状态（即双圈状态），故判定输入字符串合法有效。表2-3给出几个实例分析，请读者仔细理解。

表2-3 识别实型常量的实例分析

请读者自行补充表2-3中空白区域，以加深对转换图使用方法的理解。只有理解了转换图与普通流程图之间的联系，才能进行词法分析器的设计。Neo Pascal语言的完整转换图将在2.3节详细分析。