从第2讲到第15讲，建立了微积分的基本概念和理论.在这14讲里，没有用到极限概念，没有用到实数理论，和传统的教程很不一样.

一路走来，好像也比较严谨.

认真想想，仔细想想，有没有漏洞？有没有需要说清楚的地方？

老实说，还是有些地方应当进一步说清楚.

例如，用lnx的反函数定义了指数函数ex，然后说ex的定义域是（－∞，＋∞），这有什么依据呢？根据反函数的概念，ex的定义域是lnx的值域，怎么知道lnx的值域是全体实数的集合呢？会不会缺少几个点？

要严谨地回答这种问题，就需要知道实数系统的性质.

很多函数的定义域是区间.区间是由实数组成的集合.实数系与有理数系相比，有什么新的特性呢？

根本的区别在于，实数系是连续的，有理数系不连续.

说有理数系不连续，是指有理数之间有很多的“缝隙”.如图18－1，设数轴上的所有的有理点组成虚线OX.作边长为1的正方形OABC，以O为心过点B作圆弧穿过OX，但圆弧不可能与虚线OX相交，因为圆的半径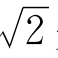是无理数！圆弧从密密麻麻的有理数之间穿过而不碰上任何一个有理数，说明有理数系在这里有缝隙.

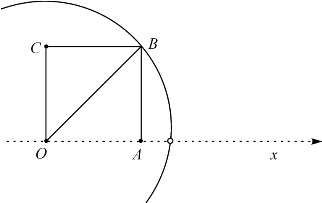
图18－1　圆弧穿过有理数之间的缝隙

把有理数系的所有缝隙都用无理数填上，就得到了实数系，怎样用数学的语言说明所有缝隙都填上了呢？下面做一个思想实验.

设想所有的实数组成了连续的天衣无缝的数直线.用一把无比锋利的大刀来砍这条直线.因为无缝隙，所以就砍在某个点P上；因为直线很细，所以就在点P处砍成了两段，如图18－2.那么，点P在哪一段上呢？

图18－2　砍断数直线的思想实验

只能说，不在左边，就在右边；两边都有或者都没有是不可能的.这里得到的结论，是实数系区别于有理数系的基本特征：

关于实数系连续性的戴德金公理 把全体实数分成A、B两个非空集合.如果对任意的x∈A和y∈B总有x＜y，则A中有最大数或B中有最小数，两者必居其一，且仅居其一.

想一想，有理数系有这样的性质吗？

从戴德金公理，可以推出一个更好用的命题：

命题18.1 （确界定理）非空有上界的实数集合S必有最小上界，非空有下界的实数集合S必有最大下界.

证明 先证明非空有上界的实数集合S必有最小上界.

设S的所有上界组成集B，其余的实数构成集A，则对任意的x∈A和y∈B总有x＜y，由戴德金公理可知A中有最大数或B中有最小数.

若a∈A，则a不是S的上界，从而有c∈S使a＜c，于是a＜∈A，这证明A中没有最大数；于是B中有最小数，即S有最小上界.

设非空实数集合U有下界m，则所有U中元素的相反数构成的集合V有上界－m，由已经证明的结论知V有最小上界b，则－b显然是U的最大下界，定理获证.

由于最小上界也叫做上确界，最大下界也叫做下确界，所以上述命题常被称为确界定理，

容易证明，确界定理等价于戴德金公理.也就是说，可以把命题18.1作为实数公理来代替戴德金公理，这时戴德金公理就成为一条定理.

确界定理有什么用？换句话，实数的基本性质戴德金公理有何用？

最有说服力的案例，是下面要讲的连续函数介值定理.

在命题5.5中证明了差商有界函数的连续性，并且阐述了函数连续性的含意.特别是连续函数的局部保号性：连续函数f（x）若在一点处函数值为正，则在此点某邻域均为正；若在一点处函数值为负，则在此点某邻域均为负；更一般地，若连续函数f（x）在x＝u处函数值f（u）属于某开区间Δ，则在x＝u某邻域的函数值均属于此开区间Δ，这个性质可以看成是连续函数的定义，

从这样的连续函数定义容易推出，连续函数的和、差、积、商（分母不为0）仍然是连续函数，两个连续函数的复合函数仍是连续函数.

从连续函数的局部保号性，推出下面非常直观的结果.

命题18.2 （连续函数的介值定理）设函数f（x）在[a，b]上连续且f（a）·f（b）＜0，则有c∈（a，b）使f（c）＝0.（图18－3）.

分析 函数f（x）在[a，b]两端正负不同，x从一端连续变化到另一端的过程中必有一个转变符号之点，此点外函数值应为0.据此有下列证明.

证明 不妨设f（a）＜0而f（b）＞0.设[a，b]上所有使f（x）＜0的点x构成集合A，则A非空有上界.由确界定理，A有最小上界x＝c.于是在点c的任意领域f（x）必然有正有负.于是由连续函数保号性，f（c）既不能为正也不能为负，只可能有f（c）＝0，证毕.

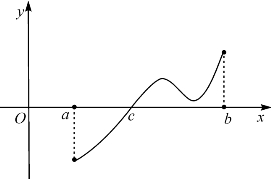
图18－3　介值定理示意

推论 设函数F（x）在[a，b]上连续，则F（x）在[a，b]上取到F（a）与F（b）之间的所有实数.

证明 为确定不妨设F（a）＜V＜F（b），往证有c∈（a，b）使f（c）＝V.只要令f（x）＝F（x）－V，则f（x）在[a，b]上连续且f（a）·f（b）＜0，由介值定理有c∈（a，b）使f（c）＝0，即F（c）＝V.推论得证.

介值定理是用二分法求函数零点的理论根据.

现在可以回答本讲开始提出的反函数存在问题了.(www.daowen.com)

命题18.3 （反函数存在性）设函数F（x）在[a，b]上连续而且严格单调，分别记A、B为F（a）、F（b）中较小者和较大者，则有唯一的定义于[A，B]的函数G（x），使对任意x∈[A，B]有F（G（x））＝x；且G（x）严格单调，值域为[a，b]，对任意x∈[a，b]有G（F（x））＝x.

证明 根据条件，当F（x）递增时令G（A）＝a而G（B）＝b，当F（x）递减时令G（A）＝b而G（B）＝a；对于x∈（A，B），应用介值定理及其推论可知有c∈（a，b）使F（c）＝x，定义G（x）＝c.这样就在[A，B]上定义了函数G（x）.由定义知道F（G（x））＝F（c）＝x.

下面证明定义于[A，B]且满足F（G（x））＝x的函数G（x）是唯一的.设有[A，B]上的函数H（x）也满足F（H（x））＝x，则对任意的u∈（A，B）有

由F（x）严格单调得G（u）＝H（u），这证明了唯一性.

函数F（x）在[a，b]上递增或递减分别等价于对任意[a，b]上两点u和v，（F（u）－F（v））（u－v）恒正或恒负，取u＝G（x）和v＝G（y）代入得

这表明函数F（x）在[a，b]上递增或递减分别等价于G（x）在[A，B]上递增或递减，于是G（x）值域显然为[a，b].最后，在F（G（x））＝x中取u＝G（x）得u＝G（x）＝G（F（G（x））＝G（F（u））.证毕.

在上述定理中的函数G（x）叫做函数F（x）在[a，b]上的反函数.

从本节推理过程看到，在中学数学课程中习以为常的一些断言，要严谨地说清楚还是颇费口舌的.同时也澄清了，要说清楚仅仅需要增加一条命题，即戴德金公理或确界定理.

从介值定理可以得出不少有用的推论，例如

区间上的不动点定理 若f（x）在[a，b]上连续，且当x∈[a，b]时有f（x）∈[a，b]，则有c∈[a，b]使f（c）＝c.

道理很简单，从f（x）∈[a，b]可知f（a）≥a和f（b）≤b.取g（x）＝f（x）－x则有g（a）≥0和g（b）≤0.由介值定理有c∈[a，b]使g（c）＝0即f（c）＝c.

前面讨论过函数的最值问题.什么样的函数一定有最值呢？下面的命题基本上解决了这个问题.

命题18.4 （闭区间上连续函数的最值定理）若f（x）在闭区间[a，b]上的连续函数，则f（x）在[a，b]上取到最大值与最小值.

证明 先证明f（x）在[a，b]上取到最大值.

为方便，不妨对x＞b令f（x）＝f（b），即将f（x）定义域扩展到[a，＋∞）.

用反证法，设f（x）在[a，b]上取不到最大值.

考虑区间[a，c].如果存在一点u，使f（u）大于f在[a，c]所取的一切值，则称c是好点.

显然a是好点.若不然，f（a）便成为最大值了.又若b是好点，则与好点的定义矛盾，故好点集非空有上界，设y是其最小上界.

由f（y）不是最大值，故有v，使得f（v）＞f（y）.由连续函数局部保号性，存在α＜y＜β使对区间[α，β]中的任意一点x，都有f（x）＜f（v）.

由于y是好点集的最小上界，故存在w使得f（w）大于f在[a，α]上的一切值.取f（w）与f（v）之中较大者记为f（p），则f（p）大于f在[α，β]上的值，于是β为好点，这与y是好点集的上界矛盾.于是f（x）在[a，b]上取到最大值.

因为－f（x）在闭区间[a，b]上也连续，所以－f（x）在[a，b]上有最大值，记为－f（x0）.显然，f（x）在[a，b]上取到最小值f（x0）.证毕.

推论1 （闭区间上连续函数有界性）若函数f（x）在闭区间[a，b]上连续，则f（x）在闭区间[a，b]上有界.

推论2 在闭区间[a，b]上的正值连续函数必有正的下界.（特别地，在闭区间[a，b]上差商有界的正值函数必有正的下界.）

现在可以证明第10讲里提出的反函数求导公式了.

命题18.5 （即命题10.5）设F（x）在[a，b]上强可导且对任意x∈[a，b]有F′（x）≠0.则其反函数G（x）强可导且有

证明 注意到强可导函数的导数差商有界，所以F′（x）在[a，b]上连续.于是从F′（x）≠0可知F′（x）在[a，b]上恒正或恒负，否则由介值定理推出F′（x）在[a，b]上某点为0.为确定，不妨设F′（x）在[a，b]上恒正，从而F（x）在[a，b]上单调递增且连续，由命题18.3可知有在[F（a），F（b）]上单调递增的函数G（x）满足F（G（x））＝x，即G（x）和F（x）互为反函数.由命题5.5可知是G（x）的乙函数，于是只要证明它差商有界即可.

由命题18.4（闭区间上连续函数的最值定理）可知F′（x）在[a，b]上取到最小值m＝F′（c）＞0，由命题5.2之（iii）可知差商有界；又由乙函数性质有|F（u）－F（v）|≥F′（p）|u－v|≥F′（c）|u－v|＝m|u－v|，故由命题5.4知G（x）差商有界，再由命题5.3推出差商有界.证毕.

在第16讲中提到，连续函数或单调函数的积分系统如果存在必然是唯一，至于是否存在，则没有回答.

有了确界定理，可以解决这个问题了.

下面说明解决此问题的主要步骤方法，详细推导从略.

设f（x）定义于区间I，对任意[u，v]⊆I，设f（x）是[u，v]上的有界函数.如果[u，v]上的逐段线性函数g（x）≤f（x），称它是f（x）的一个下函数；如果[u，v]上的逐段线性函数g（x）≥f（x），称它是f（x）的一个上函数；上函数和下函数在[u，v]上显然都可积.所有上函数在[u，v]上的定积分组成有下界的实数集，记其最大下界为H（u，v）；所有下函数在[u，v]上的定积分组成有上界的实数集，记其最小上界为L（u，v）.显然有不等式L（u，v）≤H（u，v）.可以证明（见《直来直去的微积分》定理17.2、17－7和17－8），如果L（u，v）＝H（u，v），取S（u，v）＝H（u，v）＝L（u，v），则S（u，v）是f（x）在区间I上的唯一积分系统.

具体说来，容易证明若f（x）为逐段连续或单调的函数，总有L（u，v）＝H（u，v）.所以逐段连续或单调的函数在闭区间上可积.

微积分的内容博大精深，本书所提供的仅仅是一元微积分的基本理论和方法.我们把讨论的范围限制于导数为差商有界函数的函数类，建立了一个不依赖极限理论的严谨的一元微积分体系.如果不做存在性的讨论（如反函数存在性，定积分存在性），这个体系也不依赖于实数理论.若要说清存在性问题，则只要承认“有上界的数集合必有最小上界”就够了.

把书中关于强可导函数的条件稍微放宽，就是连续可导函数类.这里的体系和方法都可以推广到连续可导函数类，仍然不必用到极限的概念和方法.

但是，极限的概念和方法毕竟是高等数学的重要部分.尽管不用它可以建立微积分，但涉及无穷的推理和计算仍要用到极限.例如，数列极限的计算当然离不开极限的概念；又如，无穷级数、无穷积分的定义也依赖极限概念；甚至研究函数曲线性质时涉及的渐近线也依赖极限概念.所以极限概念还是有必要学习.

但是，如果不依赖极限就严谨地掌握了微积分的基本内容，在此基础上学习极限就会更容易.对于中学生而言，基本掌握了不用极限的微积分，将来在大学里学习传统的微积分时，会理解得更深刻.