牛顿—莱布尼兹公式的用处不仅是计算面积.只要所求的量满足所积分系统的两个条件（可分性，中值性），都可以使用这个公式.

曲边梯形的面积是定积分最基本也是最简单的几何模型.实际上，根据积分系统的定义，只要是依赖于两个参数且满足可加性条件的量S（u，v），就可以考虑用定积分概念和微积分基本定理来计算它.为此先要确定一个使S（u，v）满足中值性条件的函数f（x），再找到函数F（x）使有F′（x）＝f（x），就可以应用微积分基本定理求出S（u，v）＝＝F（v）－F（u）.

例题17－1 （旋转体的体积）设[a，b]上的函数y＝F（x）的曲线在x轴上方.该曲线形成的曲边梯形绕x轴旋转一周形成一旋转体（图17－1），求此旋转体的体积.

解 如图，旋转体在平面x＝u和x＝v之间部分的体积S（u，v）关于参数u和v显然满足可加性.想象把这部分体积折合成高为v－u的圆柱，则圆柱的半径必在[u，v]上的两个函数值F（p）和F（q）之间，即

于是可取g（x）＝πF2（x）为被积函数，得到这部分旋转体体积表达式

图17－1　曲边梯形旋转一周形成的旋转体

考虑（17－2）中F（x）＝kx＋c的特殊情形，设k＞0，c＞0，这时F（x）的图像是一线段，对应的旋转体是高为H＝v－u的圆台（图17－2显示出线段旋转生成的圆台侧面）.圆台体积S（u，v）的定积分表达式中被积函数是π（kx＋c）2.应用114公式（命题16.5）得

图17－2　线段旋转成圆台侧面

若记上底r＝ku＋c，下底R＝kv＋c，圆台体积为V（r，R，H），则得

当r＝0时得到圆锥体积公式

这和中学里所学的公式相同.

如果用SH、SL和SM分别记圆台的上底、下底和中截面的面积，则（17－3）可以写成

这个公式常常被称为拟棱柱体积公式.它不但适用于圆锥、圆台和圆柱，也适用于棱锥、棱柱和棱台.下面指出，它还适用于球台.

在（17－2）中取F（x）＝，x∈[－R，R].函数y＝F（x）的图象是半径为R而圆心在原点的半圆.它绕x轴旋转一周生成半径为R的球面.如果取区间[0，h]上的一段圆弧绕x轴旋转，则生成一个下底为球的大圆而高为h的球台的侧面，如图17－3.

图17－3　圆弧旋转成圆台侧面

按（17－2），对应的球台体积V（R，h）为

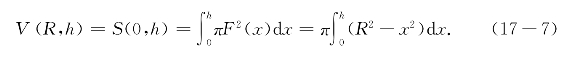
这里被积函数是二次多项式，故可用114公式得球台体积公式

上式中取h＝R得半球体积为，从而得到我们熟知但未能严谨证明的球体积V（R）的公式　

为了计算球台侧面的面积，考虑两个高相等但半径分别为R＋d和R－d的两个球台之差所形成的球带壳体的体积（图17－4）：

图17－4　球带壳体

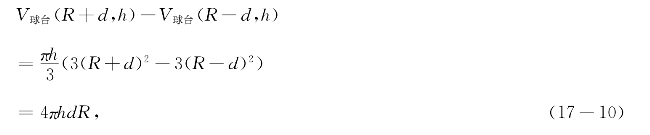
再除以壳体的厚度2d，得到半径为R高为h的球带的侧面积公式

当h＝R时即为半球的表面积，从而得到球的表面积公式

这些公式古希腊科学家阿基米德早已得到了.但我们的方法简单得多.值得一提的是，从（17－12）可知，高和底面直径相等的圆柱，其侧面积等于它的内切球的表面积（图17－5），这是阿基米德自己很满意的发现.更有趣的是，从（17－11）可知，若球的直径等于圆柱底面直径，则其球带或球冠侧面积等于等高的圆柱侧面积，如图17－6，直观上是很难使人相信的！

图17－5　高和底面直径相等的圆柱和它的内切球

图17－6　从与圆柱直径相等的球上割下的与圆柱等高的球冠

下面的例子，是定积分在物理中的应用.

例题17－2 将质量为m的物体Q从地面垂直提升到高度H，为克服地心引力需要做的功是多少？特别地，如将此物体发射使脱离地球引力，需要的初始速度是多大？

分析 物体Q与地心距离为x时，它所受的地心引力的大小为

这里G是万有引力常数，M是地球质量.设将物体从与地心距离为u提高到与地心距离为v时克服重力所做的功为w（u，v），w（u，v）显然满足可分性w（u，v）＝w（u，w）＋w（w，v）；另一方面，重力随物体与地心的距离增加而减少，故有（vu）F（v）＜w（u，v）＜（v－u）F（u）.再由F（x）差商有界性可知，若记地球半径为R，GmM＝C，由（17－13）可知将物体从地面提升到高度H时所做的功应为

(www.daowen.com)

因为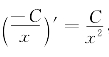，故由牛顿—莱布尼兹公式得

比值小于1，故无论上升多高所需要的能量不超过；又因为当H很大时可以任意接近于1，故可以认为此物体脱离地球引力所需要的能量为.所以物体发射的初速V应满足

比较地面重力与万有引力公式有

从而有GM＝R2g，这里重力加速度g＝9.8（米/秒2），地球半径R＝6371（千米）代入（17－16）得

所以，垂直向上发射的物体，在不计空气阻力时，只要初速达到每秒11.2千米，即可脱离地球引力.此即所谓第二宇宙速度.

前面讨论了曲边梯形面积的计算.更一般的情形，可以分割成几块来计算.

例题17－3 如图17－7，求椭圆＝1（a＞b＞0）的扇形AOB（图中阴影部分）的面积，进而计算椭圆面积.

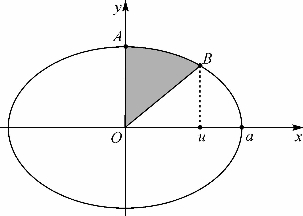
图17－7　椭圆的扇形

解 如图，A和B的横坐标分别为0和u（u＞0），则弧AB可以看成函数f（x）在[0，u]上的图象.于是要求的扇形的面积S（u）等于f（x）在[0，u]上的曲边梯形面积减去一个三角形的面积：

在网上可以找到的常用积分表里有这样的公式：

如果不放心，可以计算的导数看看是不是等于.验证无误后便用牛顿—莱布尼兹公式计算得出

上式最后一项恰为，于是所求扇形面积为

当u＝a时扇形面积是半个椭圆的面积的一半，所以

下面来讨论曲线长度的计算.

设函数f（x）在区间[a，b]上有定义，[u，v]⊆[a，b].把曲线y＝f（x）在[u，v]上的这段长度记做S（u，v），则S（u，v）显然具有可加性.

如果能够进一步说明S（u，v）是[a，b]上的某个函数g（x）的积分系统，就有了计算曲线长度的办法.关键是把函数g（x）找出来.

如果曲线y＝f（x）是一条斜率为k的线段，由勾股定理有S（u，v）＝（v－u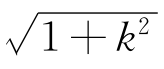）；也就是说，斜率的绝对值越大，线段越长（图17－8）.

图17－8　线段长度与斜率的关系

进一步，如果曲线y＝f（x）是一条折线，而对x∈[u，v]，组成折线的线段的斜率为k（x），则必有[u，v]上的p和q，使

也就是说，S（u，v）应当是[a，b]上的函数g（x）＝的积分系统.把对折线情形的分析推广到曲线情形，并且注意到曲线y＝f（x）在x∈[u，v]处的斜率k（x）＝f′（x），便可以合理地认为，S（u，v）是[a，b]上的函数g（x）＝的积分系统.如果y＝f（x）逐段强可导，则此积分系统唯一，且有：

于是[a，b]上曲线y＝f（x）的弧长计算公式为

例题17－4 计算曲线y＝（0≤x≤2）的弧长（图17－9）.

图17－9　曲线y＝(0≤x≤2)

解 由于f′（x）＝，故由弧长公式（17－26）知

习题17－1 函数y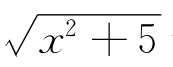＝的图像是双曲线的一支.求它在[－2，2]上的部分绕x轴旋转一周生成的立体的体积（图17－10）.

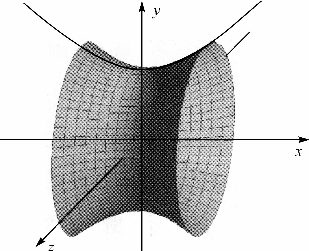
图17－10　双曲旋转面

习题17－2 假想从地球表面挖一条通道直达地心，一个小球从地表沿通道落下，求小球从地表到达地心所用的时间（注意在计算小球所受地心引力时，地球的质量不是常数.这是因为当小球在地表以下N米时，N米厚的地壳对小球的引力总和为0.这里假定地球是质量均匀的球体，半径R＝6371千米）.

习题17－3 求悬链线y＝在[0，a]部分的长度（图17－11）.

图17－11　悬链线