上面定义了函数在区间上的积分系统和定积分，自然地把积分和甲乙函数的概念联系起来，使微分和积分获得了统一的数学模型，轻松导出微积分基本定理.

历史上对微分和积分关系的认识，却经历了漫长的艰难过程，

积分的原始思想来自安蒂丰（Antiphon，约公元前480－前410）提出的计算圆面积的穷竭法.之后，不少杰出的科学家曾使用类似的思想计算面积、体积、长度和其他的物理量.其中有中国的刘徽、祖冲之、祖暅，希腊的帕普斯，荷兰的斯蒂文，意大利的伽利略，德国的开普勒，瑞士的古尔丁等.直到1635年，意大利数学家卡瓦列利的名著《用新方法促成的连续不可分量几何学》中，系统地提出计算面积等几何量的方法（卡瓦列利，Cavalieri，Francesco Bonaventura，1598—1647）.在此基础上，经过费马、罗伯瓦、托里拆利、沃利斯、帕斯卡、惠更斯、莱布尼兹集其大成的工作，才发现微积分之间的互逆关系.而真正严谨的定积分概念，即现在教科书讲的定积分概念，是1854年才由黎曼提出并详细论述的（黎曼，G.Riemann，1826—1866）.这个概念的形成，经历了长达两千年的时光，渗透着数十位卓越的数学家的心血.

下面是黎曼给出的定积分概念.

定义11 （黎曼积分）设f（x）在[a，b]上有定义，在区间[a，b]内任意插入n－1个分点

记小区间Δk＝[xk－1，xk]，k＝1，2，…，n，其长度为Δxk＝xk－xk－1.在各个小区间上取点ξk∈[xk－1，xk]并作和式

此和称为f（x）在[a，b]上（对应于分法T＝{Δk}和样本点{ξk}的黎曼和，也称积分和.

对应于分法T＝{Δk}和样本点{ξk}，可以构造一个在（xk－1，xk]上取常数值ξk的函数，叫做对应于（T，{ξk}）的阶梯函数.对应的黎曼和，就是这个阶梯函数在[a，b]上的曲边梯形的面积.

记λ（T）＝，如果不论对[a，b]上怎样的分法T，也不论ξk在[xk－1，xk]上怎样的取法，只要当λ（T）→0时上述黎曼和存在确定的极限J，则称f（x）在[a，b]上黎曼可积（在不至于混淆时简称可积），极限值

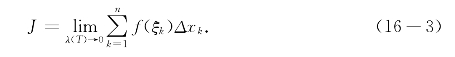
称为f（x）在[a，b]上的黎曼积分（或不至于混淆时也称定积分），记为

其中，f称为被积函数，x称为积分变量，f（x）dx称为被积表达式，[a，b]称为积分区间，a、b分别称为这个定积分的下限和上限，在不至于混淆的情形下，积分记号前面的（R）可以略去.

现在可以说明古怪的积分记号的来源了.原来它是由和式（16－2）即转化而来.经过取极限，用拉长的S即∫取代∑，用f（x）取代f（ξk），用dx取代Δxk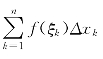，变成了.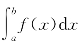

看来，基于黎曼和并依赖极限概念的定积分的定义比起本书中第15讲里的定义复杂得多，依赖极限概念的导数定义比起本书中强导数的定义来也复杂一点.把依赖于极限的导数和定积分的两个定义联系起来推导微积分基本定理，过程也要艰难得多.这是目前高中数学里不讲极限的主要原因，也是大学里多数理工科专业讲微积分不求甚解的主要原因.

图16－1中画出了[a，b]上的一个函数f（x）的曲线，区间[a，b]的一个分法T，一组样本点，图中各小矩形的面积就是对应的黎曼和中的各项，这些矩形面积的总和就是对应于此分法和样本点的黎曼和.直观看来，若分点足够密集，则不论如何取样本点，黎曼和都将非常接近这个曲边梯形的面积.

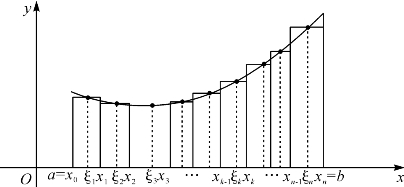
图16－1　黎曼积分和示意

由图可见，用黎曼和的极限来引入定积分概念，虽然说起来比较繁琐，其实也很直观，

那么，在第15讲里用积分系统的唯一性定义的积分，它和黎曼积分的概念有什么关系呢？两者是不是一致呢？

可以证明，两者是一致的.

命题16.1 设函数f（x）在[a，b]上有界，则f（x）在[a，b]上黎曼可积的充分必要条件是它在[a，b]上有唯一的积分系统S（u，v）；且此时有

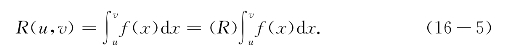
命题16.1的证明涉及根限概念和实数理论，此处从略.有兴趣的读者可参看作者《直来直去的微积分》书中17章的定理17.8.

有了命题16.1，今后就不再区别定积分和黎曼积分，在黎曼积分前面也不必标记（R）了.

在第15讲里引进的定积分和黎曼积分，字面上好像大相径庭，其实质是相通的.

设F（x）在[a，b]上强可导，F′（x）＝f（x）.在区间[a，b]内任意插入n－1个分点

a＝x0＜x1＜x2＜…＜xn－1＜xn＝b，

于是有

记小区间Δk＝[xk－1，xk]，其长度为Δxk＝xk－xk－1.根据命题6.1，对于任意的ξk∈[xk－1，xk]有

此式可以写成F（xk）－F（xk－1）－f（ξk）Δxk＝αk，从而有

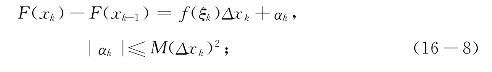
将（16－8）对k＝1，2，…，n求和得到

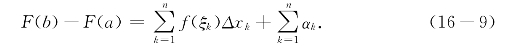
比较（16－9）与（16－6）可以发现，和式其实就是用诸f（ξk）Δxk近似地代替诸F（xk）－F（xk－1）所产生的总误差.如果诸Δxk中最大者为δ，则有

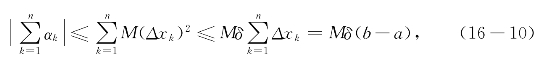
从而当区间分割越来越细时，也就是δ趋向于0时，（16－9）右端第二个和式趋向于0，而第一个和式恰好就是黎曼和，其极限正是f（x）在[a，b]上的定积分，所以（16－9）取极限得到

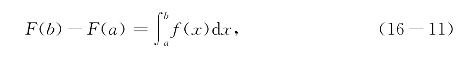
这就从黎曼和的途径得到了牛顿—莱布尼兹公式（微积分基本定理）.

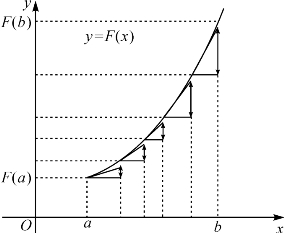
从（16－6）到（16－11），这个推导过程并不依赖图16－1.图16－1把f（x）曲线形成的曲边梯形的面积分割作为几何模型，是黎曼提出来的.林群直接考虑F（x）的曲线，提出了一个更简单的几何模型（见光明日报1997－6－27，人民日报1997－08—06或《微积分快餐》8、19、39页，或《微积分减肥快跑》），如图16－2.图中的曲线是F（x）在[a，b]上的图像，两条相邻竖虚线的距离是Δxk，两条相邻横虚线的距离是F（xk）－F（xk－1），这里的诸ξk取在小区间的左端（此处k＝1，2，3，4，5），x0＝a，x5＝b.斜的直线段是ξk处的切线，而标有双箭头的线段的长度为f（ξk）Δxk.对照图16－2再看从（16－6）到（16－11）的推导过程，感到微积分基本定理竟如此简单.

(www.daowen.com)

图16－2　微积分基本定理的林群模型

在命题15.3中，假定了f（x）是某个函数F（x）的导数，亦即假定了它有原函数，才推出了f（x）的积分系统的唯一性，

如果不假定f（x）有原函数，如何判断它对应的积分系统是否唯一呢？

下面的命题初步回答了这个问题.

命题16.2 （差商有界函数积分系统唯一性）设f（x）在区间I上差商有界，S（u，v）和R（u，v）都是f（x）在I上的积分系统，则恒有S（u，v）＝R（u，v）.

命题16.3 （单调函数积分系统唯一性）设f（x）在区间I上单调，S（u，v）和R（u，v）都是f（x）在I上的积分系统，则恒有S（u，v）＝R（u，v）.

如果f（x）的定义区间可以分成有限个闭区间，使得f（x）在每个闭区间上差商有界或单调，称它为逐段差商有界或单调函数.下面的定理扩大了上述结论使用的范围.

命题16.4 若f（x）和g（x）在I上都是逐段连续或单调的函数，则函数y＝f（x）＋g（x）在I上的任意两个积分系统都相同.

关于这些命题的证明，有兴趣的读者可参看作者《直来直去的微积分》第6章最后一节.

本讲所介绍的黎曼和，不仅用于积分的理论探索，也可以用来计算或估计函数的定积分.

对于不超过3次的多项式的定积分，有一个非常简单的公式.

命题16.5 （114公式）设f（x）＝ax3＋bx2＋cx＋d，则在任意区间[a，b]上有

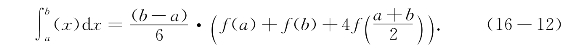
证明 只要分别对函数y＝x3、y＝x2、y＝x和y＝1来验证这个公式即可.验证过程如下

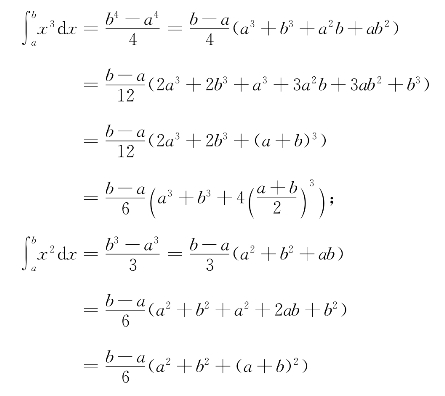
这就证明了所要的（16－12）.

这个公式以后简称114公式，在几何中常用于体积计算，下一讲还会谈到，用114公式计算其他函数的定积分，得到的不是准确值而是近似值.

例题16－1 分别用黎曼和的方法和114公式计算区间[0，1]上曲线y＝x2之下的区域的面积（图16－3）.

图16－3　[0，1]上曲线y＝x2下的面积

解 （i）黎曼和方法：将区间[0，1]等分为n段，分点为

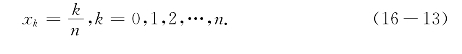
由函数y＝x2在[0，1]上的递增性，可知

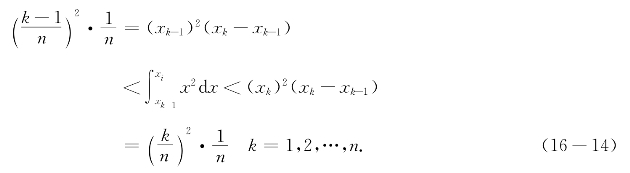
将上式对k＝1，2，…，n相加得

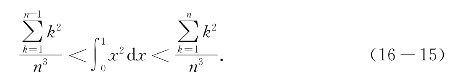
利用不等式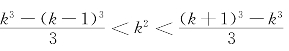代入上式得

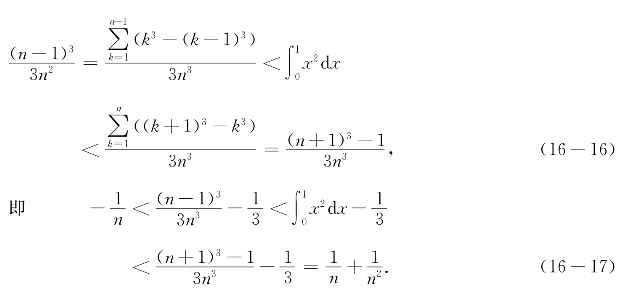
因为n可以任意大，故＝0，即所求面积为.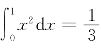

（ii）114方法：

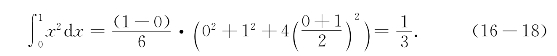
例题16－2 用114方法计算区间上曲线y＝sinx之下的区域的面积（图16－4）.

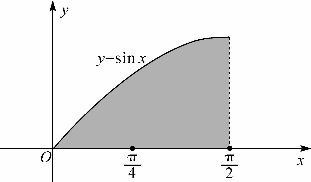
16－4　上曲线y＝sinx下的区域

解 使用114公式得

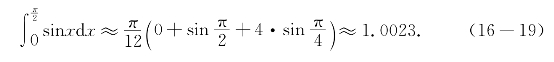
如果把积分区间分成两段计算，则有

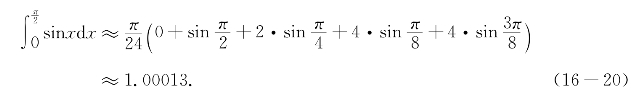
由前面例题15－4知此面积为1，可见所得结果相当精确.

习题16－1 用微积分基本定理和114公式计算下列定积分

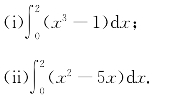
习题16－2 分别用泰勒公式和114公式计算ln2＝的值，要求误差不超过0.0001（可利用泰勒余项估计其误差）.