本书一开始就提到,如何计算任意曲线包围的面积,直到17世纪初还是数学家面前的难题.微积分的诞生使这个难题迎刃而解.
一般说来,任意曲线包围的区域总能用直线分割成若干矩形和一些“曲边梯形”(图15-1),所以问题最后归结为曲边梯形面积的计算.在第2讲谈到“曲边梯形”面积和估值不等式的联系;在第9讲中,更利用曲边梯形面积与估值不等式引进了对数函数lnx.为了进行更严谨的讨论,必须说清楚什么是曲边梯形的面积.
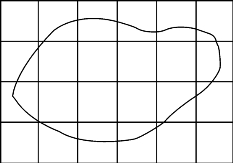
图15-1 曲线包围的区域被分割成矩形和曲边梯形
给了区间I上的函数f(x),对应于I中任意两点u<v,f(x)在[u,v]上的曲边梯形的“代数面积”(如图15-2,在x轴上方部分面积为正,下方部分面积为负,取总和),可以看成是某个二元函数S(u,v)的值.基于一般的面积概念,S(u,v)应当满足两个条件.一个条件是面积的可加性:[u,v]上的面积加上[v,w]上的面积,等于[u,w]上的面积;第二个条件是,[u,v]上的面积和区间[u,v]的长度之比,应当是f(x)在[u,v]上的“平均值”.根据面积的这些直观性质,抽象出下面的定义.
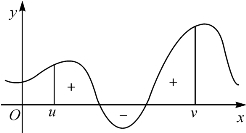
图15-2 区间[u,v]上曲边梯形的代数面积
定义10 (积分系统和定积分)设f(x)在区间I上有定义;如果有一个二元函数S(u,v)(u∈I,v∈I),满足
(i)可加性:对I上任意的u,v,w有
![]()
(ii)中值性:对I上任意的u<v,在[u,v]上必有两点p和q使
![]()
则称S(u,v)是f(x)在I上的一个积分系统.
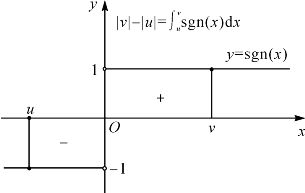
如果f(x)在I上有唯一的积分系统S(u,v),则称f(x)在(I的子区间)[u,v]上可积,并称数值S(u,v)是f(x)在[u,v]上的定积分,记作![]() .表达式中的f(x)叫做被积函数,x叫做积分变量,u和v分别叫做积分的下限和上限.用不同于u,v的其他字母(如t)来代替x时,S(u,v)数值不变.
.表达式中的f(x)叫做被积函数,x叫做积分变量,u和v分别叫做积分的下限和上限.用不同于u,v的其他字母(如t)来代替x时,S(u,v)数值不变.
根据定义容易得出
命题15.1 若S(u,v)是一个积分系统,则
(i)S(u,u)=0;
(ii)S(u,v)=-S(v,u). (15-3)
证明 (i)由S(u,u)+S(u,v)=S(u,v)推出S(u,u)=0;
(ii)由S(u,v)+S(v,u)=S(u,u)=0推出S(u,v)=-S(v,u).
命题15.2 设S(u,v)是f(x)在I上的一个积分系统,c是I上的一个点,令F(x)=S(c,x),则在I上f(x)是F(x)的乙函数;
反过来,若在I上f(x)是F(x)的乙函数,令S(u,v)=F(v)-F(u),则S(u,v)是f(x)在I上的一个积分系统.
证明 设S(u,v)是f(x)在I上的一个积分系统且F(x)=S(c,x),则由可加性有S(u,v)=S(c,v)-S(c,u)=F(v)-F(u),再由中值性可知f(x)是F(x)的乙函数.
反过来,若在I上f(x)是F(x)的乙函数,令s(u,v)=F(v)-F(u),则由S(u,v)+S(v,w)=F(v)-F(u)+F(w)-F(v)=F(w)-F(u)=S(u,w)
可知S(u,v)满足可加性,再由乙函数定义得S(u,v)满足中值性.证毕.
定积分除了满足前述定义外,还有下述基本性质:
(i)若f(x)和g(x)都在[a,b]可积,则对于任意实数α和β,函数αf(x)+βg(x)也在[a,b]可积,且
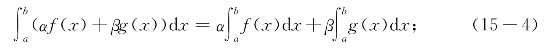
(ii)若f(x)在[a,b]可积,则函数|f(x)|也在[a,b]可积,且
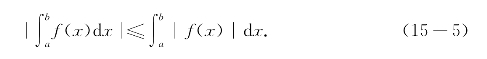
这些性质的证明从略,
性急的读者可以跳过下面的两个例题,了解微积分基本定理.
例题15-1 求证区间I上的常数函数f(x)=c有唯一的积分系统S(u,v),并计算S(u,v)=![]() .
.
证明 根据中值性有
c(v-u)=f(p)(v-u)≤S(u,v)≤f(q)(v-u)=c(v-u).
从而
S(u,v)=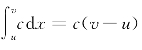 (其几何意义如图15-3).
(其几何意义如图15-3).
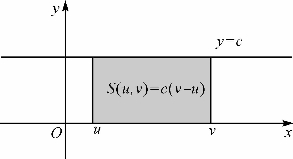
图15-3 常数函数f(x)=c的定积分
例题15-2 设f(x)=sgn(x),S(u,v)=|v|-|u|,则在任意区间I上,S(u,v)是f(x)的唯一积分系统,即
![]()
证明 容易验证在任意区间I上f(x)=sgn(x)是F(x)=|x|的乙函数(习题2-7),从而由命题15.2知道S(u,v)=|v|-|u|是f(x)=sgn(x)的一个积分系统.
下面证明S(u,v)=|v|-|u|是f(x)=sgn(x)的唯一的积分系统.
设R(u,v)也是f(x)=sgn(x)的一个积分系统,往证R(u,v)=S(u,v).由可分性有R(u,v)=R(0,v)-R(0,u)和S(u,v)=S(0,v)-S(0,u),故只要证明对任意的x有R(0,x)=S(0,x)即可.
用反证法.设有c使得R(0,c)≠S(0,c),记A=|R(0,c)-S(0,c)|>0.此时显然有c≠0.取正整数n>![]() ,则
,则![]() 和c同为正数或同为负数.由例题15-1有
和c同为正数或同为负数.由例题15-1有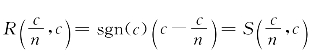 ,故得
,故得
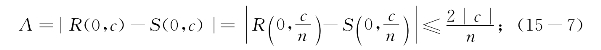
这与n>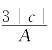 矛盾,从而否定了反证法假设R(0,c)≠S(0,c),证毕.
矛盾,从而否定了反证法假设R(0,c)≠S(0,c),证毕.
例题15-2的几何意义如图15-4.
下面的定理,标志着微积分的诞生.
命题15.3 (微积分基本定理)设F(x)在I上强可导,F′(x)=f(x).令S(u,v)=F(v)-F(u),则S(u,v)是f(x)在I上的唯一积分系统,从而有
 (https://www.daowen.com)
(https://www.daowen.com)
图15-4 符号函数f(x)=sgn(x)的定积分
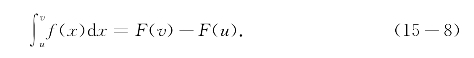
(这个等式就是著名的牛顿—莱布尼兹公式.)
证明 由命题6.4,F′(x)=f(x)是F(x)的乙函数.由命题15.2推出S(u,v)=F(v)-F(u)是f(x)在I上的积分系统.
下面只需要证明S(u,v)是f(x)在I上的唯一积分系统.
设R(u,v)也是f(x)在I上的积分系统.取I上任一定点c,令G(x)=R(c,x),则由命题15.2,在I上f(x)也是G(x)的乙函数;又由命题6.4知f(x)在I上差商有界,且G′(x)=f(x)=F′(x).
于是(G(x)-F(x))′=0,导数为0,故在I上F(u)-G(u)=F(v)-G(v)为常数,故有R(u,v)=G(v)-G(u)=F(v)-F(u)=S(u,v),这证明了S(u,v)是f(x)在I上的唯一积分系统,由定义知道定积分记号合理,从而由S(u,v)=F(v)-F(u)得所要的等式,证毕.
若f(x)是F(x)的导数,则称F(x)是f(x)的原函数.牛顿—莱布尼兹公式表明,只要找到f(x)的一个原函数,就能够轻易地求出y=f(x)构成的曲边梯形的面积.这一举解决了大量的面积计算问题.
例题15-3 如图15-5,抛物线y=x2和直线y=x+2交于P和Q两点,求线段PQ所对的抛物线弓形的面积.
解 如图15-5,所求弓形面积等于梯形ABPQ减去抛物线下阴影部分面积之差.设阴影部分面积为S,由于f(x)=x2的原函数是F(x)=![]() ,根据微积分基本定理得
,根据微积分基本定理得
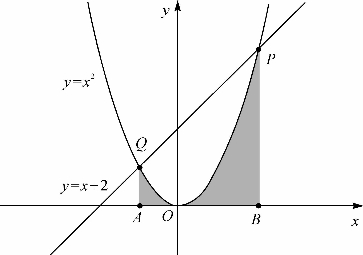
图15-5 抛物线下的面积
![]()
容易算出梯形ABPQ面积为![]() ,故所求弓形面积为
,故所求弓形面积为![]() .
.
这里和以后用记号F(x)![]() 表示F(b)-F(a).其中变量x可以代之以其他字母变量.
表示F(b)-F(a).其中变量x可以代之以其他字母变量.
例题15-4 求函数y=sinx的曲线在区间[a,b]形成的曲边梯形的代数面积.
解 由于(-cosx)′=sinx,根据微积分基本定理可知所求代数面积为
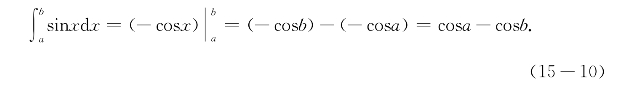
取(15-10)的特例,令a=0,b=π,求得正弦曲线在[0,π]上的弓形面积(图15-6)为
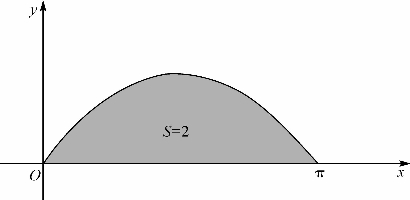
图15-6 正弦曲线在[0,π]上的弓形面积
![]()
曲边梯形的面积是定积分最基本的几何模型,也是最初步的应用.后面还会举出它在物理和几何中更多的应用.
为了应用微积分基本定理(牛顿—莱布尼兹公式),常常要找出已知函数的原函数即甲函数,也就是问已知函数是谁的导数.
若F(x)是f(x)的一个原函数,C是任意常数,则F(x)+C显然也是f(x)的原函数.
如果G(x)也是f(x)的原函数,则(F(x)-G(x))′=0,从而F(x)-G(x)是常数.这表明f(x)的所有的原函数都可以表示成F(x)+C的形式.
求原函数和求导数这两个运算互为逆运算,就像乘法和除法.数学中互逆的一对运算,常常是一个容易一个难.乘法容易除法难,求导数容易求原函数难.数学研究表明,有些初等函数的原函数不再是初等函数,可以用其他方法计算其定积分.在大学数学课程中,将学习更多求原函数和求定积分的方法和技巧,即所谓积分法.
若F(x)是f(x)一个原函数,f(x)的所有原函数之集F(x)+C叫做f(x)的不定积分,记作∫f(x)dx,即
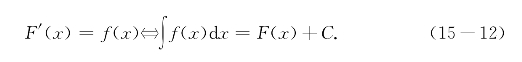
这里∫叫做积分号,f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式,C叫做积分常数.
根据微分的定义,得到
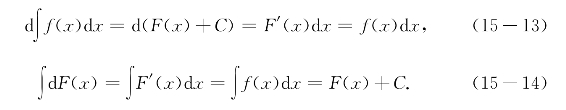
这里显示出两个运算符号d和∫的互逆关系.
有不少数学软件可以用来在计算机上求函数的不定积分,即求原函数.手算不定积分可以查阅不定积分表.
根据基本初等函数求导公式,可得如下不定积分公式,这些公式构成基本积分表.
基本积分表
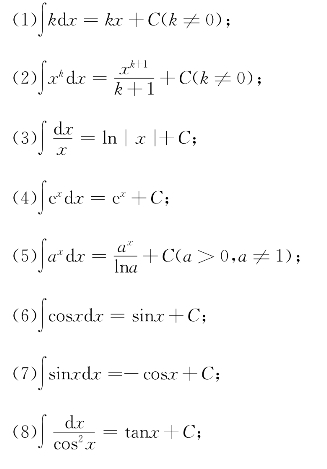
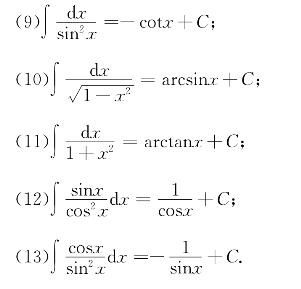
直接应用基本积分表,可以求出一些函数的不定积分.在因特网上容易找到免费下载的常用积分表.在计算机上用数学软件求函数的原函数也很容易,但是也有很多函数的原函数不能用初等函数表示.
例题15-5 应用基本积分表求下列不定积分

习题15-1 求证区间I上的一次函数f(x)=k·x+c有唯一的积分系统S(u,v),并计算S(u,v)=![]() dx.
dx.
习题15-2 设floor(x)=[x]([x]表示x的整数部分,即不超过x的最大整数,例如[3.42]=3,[5]=5,[-2.7]=-3),试证在任意区间I上,floor(x)=[x]有唯一积分系统S(u,v),并计算S(u,v)=![]() .
.
习题15-3 如图15-7,抛物线2y=x2和y2=2x交于P和Q两点,求两段以P和Q为端点的曲线围成的区域的面积(图上阴影部分).
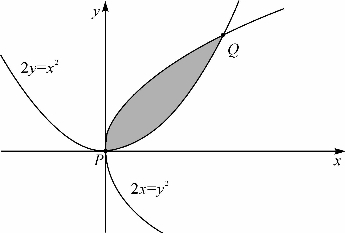
图15-7 两条抛物线相交形成的区域
习题15-4 求函数y=2x的曲线在区间[-1,1]上形成的曲边梯形的代数面积.
习题15-5 应用基本积分表求下列不定积分
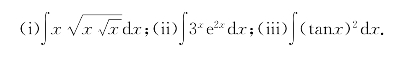
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






