知道了一个函数y＝F（x）的表达式，如何根据给定的x的值尽可能准确地求出F（x）的值呢？这个问题的现实重要性和理论意义是不言而喻的.

有些函数，根据表达式可以通过加减乘除来求函数值.例如多项式函数和分式函数.但是另一些函数，像三角函数、对数函数、指数函数等，从表达式看不出求函数值的具体步骤.在没有微积分的年代，数学家曾经花费大量的时间和精力编制这些函数的函数表，以满足天文、航海等实际应用的需求.微积分的发展，为计算函数值提供了有力的方法，其中最重要也是最常用的，就是泰勒公式（泰勒，B.Taylor，英国数学家，1685—1731）.

泰勒公式最简单的情形，可以从强导数的定义推出.

回顾强可导的定义（定义5）可知，若函数f（x）在[a，b]上的强导数为f′（x），则有正数M使对[a，b]上任两点u和u＋h成立不等式（6－6）：

记u＋h＝x，再令

R1（x，u）＝f（x）－f（u）－f′（u）（x－u）

则有

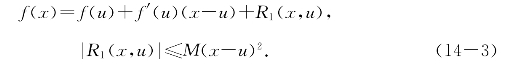
式（14－3）表明，如果x和u很接近，可以用一次函数f（u）＋f′（u）（x－u）作为f（x）的近似值，其误差的绝对值不超过M（x－u）2.在例题1－2、2－2、6－5中，正是用这种思路估计了几个函数在某些点处的值.

一次函数f（u）＋f′（u）（x－u）和f（x）之间有什么关系呢？

容易看出，它们在x＝u处有相同的函数值和相同的导数值.

一次函数y＝f（u）＋f′（u）（x－u）的图象是直线，它就是曲线y＝f（x）在点（u，f（u））处的切线.直线和曲线一般总不会太接近.如果用二次函数以至更高次的多项式作为函数f（x）的近似值，看来应当有更好的效果.这样就引出了泰勒多项式的概念.

泰勒多项式的概念涉及函数的高阶导数.

前面讨论函数的凸性时，用到了二阶导数.

函数F（x）的导数F′（x）也叫一阶导数.F′（x）的导数叫二阶导数，记作F″（x）.如果F″（x）可导，其导数叫做F（x）的三阶导数，记做F‴（x）或F（3）（x）.一般说来，可以归纳地定义：记F（0）（x）＝F（x），F（1）（x）＝F′（x）；当n＞1时若F（n－1）（x）可导则定义

并称F（n）（x）为F（x）的n阶导数.

定义9 设F（x）在区间I有n阶导数（n＞0），u∈I.多项式

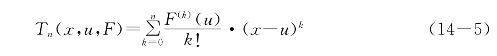
叫做F（x）在x＝u处的n阶泰勒多项式.而

叫做F（x）在x＝u处的n阶泰勒展开的余项，或n阶泰勒余项.

在不至于混淆时，可以简单地用Rn（x）和Tn（x）或Rn（x，F）和Tn（x，F）分别表示Rn（x，u，F）和Tn（x，u，F）.

容易验证，Rn（u）＝F（u），并且对k＝1，…，n有R（k）n（u）＝F（k）（u）.也就是说，所谓F（x）在x＝u处的n阶泰勒多项式Rn（x），是这样的不超过n次的多项式，它在x＝u处的函数值和不超过n阶的导数值分别和F（x）的函数值和不超过n阶的导数值相等.

根据（14－6），有

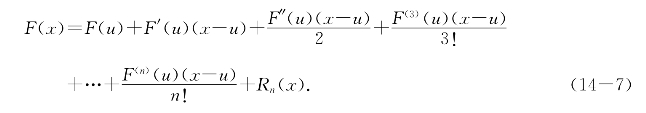
这个等式叫做F（x）在x＝u处的n阶泰勒展开式，F（x）在x＝0处的泰勒展开式也叫做F（x）的马克劳林展开式（马克劳林，C.Maclaurin，英国数学家，1698—1746）.

如果余项|Rn（x）|很小，泰勒公式就提供了用四则运算计算函数值的一个有效的方法.因此，余项的估计很重要.估计余项的方法不止一种，下面的方法仅仅用到“导数正则函数增”的基本知识.

命题14.1 设F（x）和G（x）在[a，b]上可导，如果对一切x∈[a，b]有F′（x）≤G′（x），则对一切x∈[a，b]有

证明 令H（x）＝G（x）－F（x），则对一切x∈[a，b]有H′（x）＝G′（x）－F′（x））≥0，故H（x）在[a，b]上单调不减，从而H（x）≥H（a），即（14－8），证毕.

命题14—2 （预备泰勒定理）设H（x）在[a，b]上n＋1阶可导，且

（i）k＝0，1，2，…，n时，有H（k）（a）＝0；

（ii）在[a，b]上有m≤H（n＋1）（x）≤M.

则对x∈[a，b]有

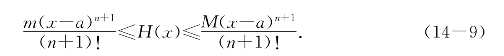
证明 先对k＝0，1，2，…，n＋1作不完全归纳来证明

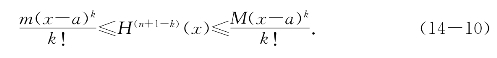
当k＝0时，由条件（ii）在[a，b]上有m≤H（n＋1）（x）≤M；

设k＜n＋1时有（14－10），则由命题14.1对k＋1有

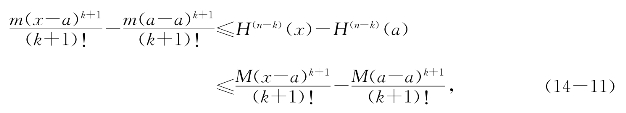
由条件（i）也就是

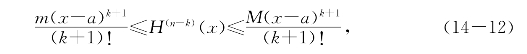
由数学归纳法，（14－10）对k＝0，1，2，…，n＋1成立.特别当k＝n＋1时得到要证明的（14－9），证毕.

现在可以轻松得到泰勒展开式的余项估计了.

命题14.3 （泰勒定理）设F（x）在[a，b]上n＋1阶可导，且在[a，b]上有|F（n＋1）（x）|≤M，则对[a，b]上任意点u和x，有泰勒展开式

并且(www.daowen.com)

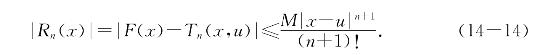
证明 令H（x）＝F（x）－Tn（x，u），易验证H（x）在[u，b]上满足命题14.2中的条件，从而当x∈[u，b]时，有（14－14）成立.

当x∈[a，u]时，取G（x）＝F（－x），对G（x）在[－u，－a]上应用上述已经获证的结论，再将G回代为F，就完全证明了所要的结论，证毕.

利用泰勒公式展开多项式，若n不小于多项式的次数，则余项为0，得到准确的表达式.

例题14—1 按（x＋1）的幂展开函数F（x）＝x4－5x3＋2x2－3x＋7.

解1 容易求得

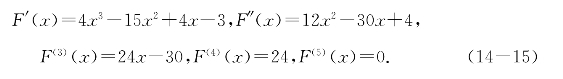
于是F（－1）＝18，F′（－1）＝－26，F″（－1）＝46，F（3）（－1）＝－54，F（4）（－1）＝24；代入泰勒多项式，注意余项为0，得到：

解2 用待定系数法，设

两端取x＝－1得A＝F（－1）＝18；

将（14－17）两端求导后取x＝－1得B＝F′（－1）＝－26；

再求导取x＝－1得2C＝F″（－1）＝46，C＝23；

再求导取x＝－1得6D＝F（3）（－1）＝－54，D＝－9；

最后显然有E＝1，从而得到同样的结果.这种方法说明了泰勒多项式的发现过程.

解3 不求导数也可以.只要设x＋1＝u，则x＝u－1，于是

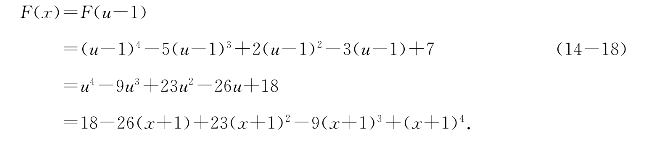
可谓殊途同归.

例题14—2 写出函数F（x）＝ex的n阶马克劳林公式，并求e的近似值，使其误差不超过10－6.

解 容易计算出

根据泰勒定理，对于任意的a≤0≤b和x∈[a，b]得

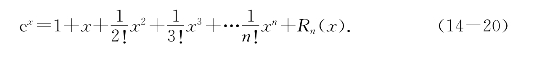
若记A＝max{|a|，|b|}，则

取x＝1，则得无理数e的近似式为

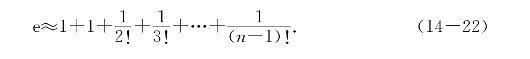
因为x＝1∈[0，1]，所以

取n＝9，可得Rn（1）＜10－6，此时e≈2.718282即为所求.

图14－1画出了函数y＝ex和它在x＝0处的前几个泰勒多项式的图像，图中粗线是y＝ex的图像，细虚线分别是其0到6价的泰勒多项式的图像，其中4、5、6阶的泰勒多项式在x＞0的部分和y＝ex很接近，从图上看不到了.

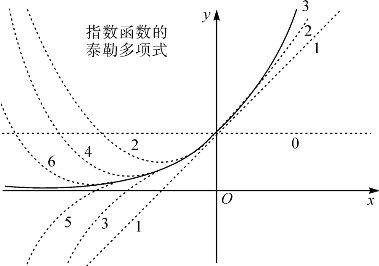
图14－1　指数函数的泰勒多项式

例题14—3 求函数F（x）＝sinx的n阶马克劳林展开式.

解 计算给出F（2n）（0）＝0，F（4n＋1）（0）＝1和F（4n＋3）（0）＝－1，故有

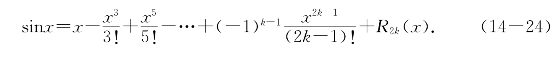
其中|R2k（x）|≤.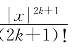

如果在（14－24）中取k＝1，则得近似公式sinx≈x，分别取k＝2，3，则可得sinx的3次和5次近似公式sinx≈x－和sinx≈x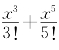－.这些和sinx越来越接近的多项式函数的曲线如图14－2.

习题14—1 按（x－1）的幂展开函数F（x）＝x4－4x3＋5x2－7x＋3，用不同的方法来做.

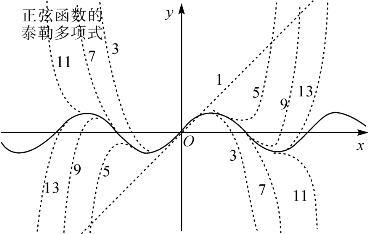
图14－2　正弦函数的秦勒多项式

习题14—2 求证

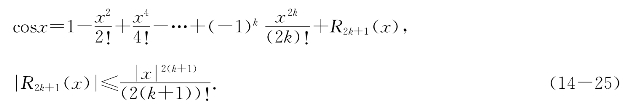
并用此式计算cos5°精确到5位有效数字.

习题14—3 求ln（1＋x）的马克劳林展开式，并估计余项.

习题14—4 求函数f（x）＝arctanx的马克劳林展开式，并利用它计算圆周率π的近似值.