给了一个初等函数的表达式，我们已经知道如何计算其微商即导数.计算的步骤可以机械化地执行.对于比较复杂的表达式，可以用计算机来求导.

求一个函数的导数的目的，是为了掌握函数的性质.例如：

（i）估计函数在某些点处所取的值，如例题1－2、2－2、6－5等；

（ii）作函数曲线的切线（其实就是确定函数在某些点附近的最简单的近似表达式），如例题3－1、3－2、3－3、8－3、12－2等；

（iii）确定函数的增减性以及最大最小值，如例题2－1、4－1、4－3、4－4、4－5、4－6、5－6等.

根据函数在某些特殊点的值和增减性，可以大体上了解函数图像的模样.但是，增减性相同的函数，其图像仍然会有很大差异，图13－1中的两条曲线弧都是单增的，但弯曲方向却完全不同，如何描述曲线弯曲方向呢？

直线不弯曲，于是曲线弯曲方向可以直线为标准作比较.在图13－1中的虚线曲线y＝g（x）上取两点作弦，两点之间的曲线在弦的上方；在实线曲线y＝f（x）上取两点作弦，两点之间的曲线在弦的下方.过两点（u，F（u））和（v，F（v））的直线方程为

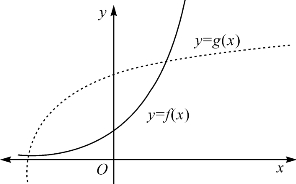
图13－1　两个递增函数的曲线凸凹性不同

故可用下面的方法刻画曲线的凸凹.

定义8 设函数F（x）在区间I有定义.对I的任意子区间（u，v），记

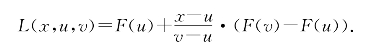
若对x∈（u，v）总有

则称函数y＝F（x）在I上是下凸的；如果上述不等式中等号总是取不到，即对x∈（u，v）总有

则称函数y＝F（x）在I是严格下凸的；

反过来，如果将不等式反向，即对x∈（u，v）总有

则称函数y＝F（x）在I是上凸的；如果对x∈（u，v）总有

则称函数y＝F（x）在I是严格上凸的.

相应地也称函数曲线是下凸的或上凸的等等，

图13－2是严格下凸函数的定义的说明.图中直线方程是

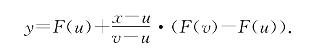
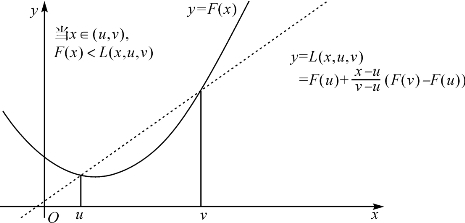
图13－2　严格下凸函数图象

关于函数的凸性，各种资料中的说法不同.有的书上称下凸的函数为“凸函数”；有的则相反，称下凸的函数为“凹函数”而称上凸的函数为“凸函数”.此外还有上凹和下凹的说法，凸向原点和凹向原点的说法.总之，阅读时要细心关注该资料本身的定义或上下文.这里采用的上凸下凸的说法，不仅符合直观，也和各种资料均不冲突，没有歧义.

另外，刻画函数凸性的不等式，也有不同的说法.不少资料上采用的定义类似于下面的表达：

设函数F（x）在区间I上定义，若对I中的任意两点u和v，和任意λ∈（0，1），都有

则称F（x）在I上是下凸的.

相应地，在不等式中改取符号＜、≥或＞，得到严格下凸、上凸和严格上凸的定义.

应当指出，不等式（13－5）和（13－1）等价，事实上，只要取点x＝λu＋（1－λ）v，则λ∈（0，1）等价于x∈（u，v），且λ＝；简单的计算表明

也就是说，基于形式（13－5）的定义和这里的定义等价.

不少书上采用另一种方式来定义函数的凸性：

若对任意u，v∈I，u≠v，总有

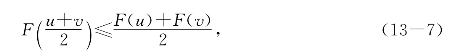
则称函数曲线y＝F（x）在I上是下凸的；

若对任意u，v∈I，u≠v，总有

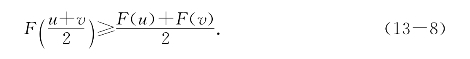
则称函数曲线y＝F（x）在I上是上凸的.

从不等式（13－5）显然能推出（13－7），反过来一般不成立.不过若限制于可导函数，能够证明两者等价.

本书定义8中的不等式，左端是曲线弧上对应于变量x的点的纵坐标，右端是曲线弧的弦上对应于变量x的点的纵坐标，直观地表示出弦与弧的上下位置关系，无需更多推导.而另外两种定义，则具有数学的简洁性.

若函数F（x）在区间I可导，其曲线上每点处就都有切线.作出曲线的切线来观察，可以发现凸凹性和切线也有关系.函数y＝F（x）在I上是下凸的，相当于曲线弧上每一点处的切线都在曲线弧之下.函数曲线y＝F（x）在I上是上凸的，相当于曲线弧上每一点处的切线都在曲线弧之上；图13－3是下凸的情形.

图13－3　下凸函数曲线的切线在下面

仔细观察容易发现，下凸曲线上每点处的切线斜率随着x的增大而增大，上凸曲线每点处的切线斜率随着x的增大而减少，如图13－4.

而函数曲线F（x）的切线斜率就是导数F′（x），这就提示我们，可用F′（x）的单调性来判断函数曲线y＝F（x）的凹凸性.经严谨论证，可得如下判定函数曲线凹凸性的方法.

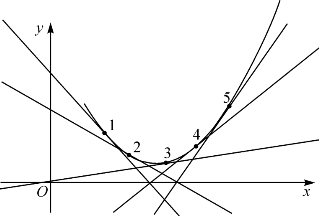
图13－4　下凸函数曲线切线斜率递增

命题13.1 设函数y＝F（x）在区间I可导，则

（i）若F′（x）在I上非减，则y＝F（x）在I上是下凸的；

若F′（x）在I上递增，则y＝F（x）在I上严格下凸；

（ii）若F′（x）在I上非增，则y＝F（x）在I上是上凸的；

若F′（x）在I上递减，则y＝F（x）在I上严格上凸.

证明 对于I中任意三点u＜x＜v，由估值不等式可知：有[u，x]中的p和q，并且有[x，v]中的r和s使有不等式(www.daowen.com)

而且若F′（x）在I上递减或递增，则y＝F（x）在I的任何子区间不可能是线性函数，从而上面的不等式可以成为严格的，即有

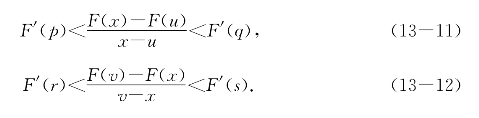
于是

（i）若F′（x）非减，则由q≤x≤r得F′（q）≤F′（r），由（13－9）和（13－10）得

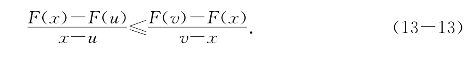
这等价于

（F（x）－F（u））（v－x）≤（F（v）－F（x））（x－u），

整理得

（v－u）F（x）≤（v－u）F（u）＋（x－u）（F（v）－F（u）），　（13－14）

两端除以（v－u）即得F（x）下凸的定义不等式.

若F′（x）递增，用（13－11）和（13－12）代替（13－9）和（13－10），同理得严格下凸定义不等式.

（ii）若F′（x）非增，则由p≤x≤s得F′（p）≥F′（s），由（13－9）和（13－10）得

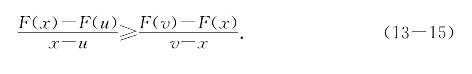
整理得

两端除以（v－u）即得F（x）上凸的定义不等式.

若F′（x）递减，用（13－11）和（13－12）代替（13－9）和（13－10）同理得严格上凸定义不等式.证毕.

函数y＝F（x）的导数F′（x）如果也可导，则由F′（x）的导数的正负可以判断其增减性.此时称F（x）二阶可导，F′（x）的导数叫做F（x）的二阶导数，记作F″（x）.因而有

命题13.2 设函数y＝F（x）在区间I上二阶强可导，若F″（x）＞0，则F（x）在区间I上严格下凸；若F″（x）＜0，则F（x）在区间I上严格上凸.

例题13—1 确定对数函数y＝logax的凸性.

解 两次求导数得

当a＞1时lna＞0从而y″＜0，由命题13.2知y＝logax严格上凸；

当a＜1时lna＜0从而y″＞0，由命题13.2知y＝logax严格下凸（图13－5）.

例题13—2 讨论函数曲线y＝x3的凹凸性.

解 两次计算导数得

当x∈（－∞，0），y″＜0，故函数y＝x3在（－∞，0）严格上凸；

图13－5　对数函数的凸性

当x∈（0，＋∞），y″＞0，故函数y＝x3在（0，＋∞）严格下凸（图13－6）.

图13－6　函数曲线的拐点

这里，函数曲线y＝x3在点（0，0）左右的凸性发生了变化.称点（0，0）为此曲线的拐点，一般说来，若函数曲线y＝F（x）在经过点（x0，F（x0））时凹凸性改变了，那么就称点（x0，F（x0））为该曲线的拐点，也说x0是函数y＝F（x）的拐点.

显然，二阶可导的函数y＝F（x）对应的曲线凹凸性发生变化的点必然是F″（x）的符号发生变化的分界点，即满足F″（x）＝0的点或二阶导数不存在的点.找出这些点，再看点的两侧F″（x）的符号是否相同，即可确定是否为拐点.

例题13—3 求函数y＝曲线的拐点.

解 求出　

这里没有使y″＝0的点，但x＝0时y″不存在.

当x＜0时y″＞0，曲线下凸；当x＞0时，y″＜0，曲线上凸.

所以点（0，0）是函数y＝曲线的拐点（图13－7）.

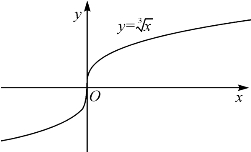
图13－7　函数y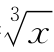＝曲线的拐点

例题13—4 确定函数y＝f（x）＝的凸性与拐点.

解 求出

使y″＝0的点为x＝±1，为方便讨论，列表如下：

函数曲线y＝的两个拐点分别是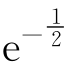（－1，）与（1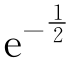）.如图13－8.

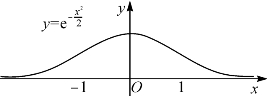
图13－8　函数曲线y＝的两个拐点

习题13—1 讨论函数y＝arctanx曲线的凸性，并确定其拐点.

习题13—2 讨论指数函数y＝ex的凸性，并证明当x≠y时有不等式ex＋ey＞ .

习题13—3 讨论函数y＝sinx曲线的凸性，并确定其拐点.

习题13—4 讨论函数y＝曲线的凸性，并确定其拐点.

习题13—5 讨论函数y＝x3－a·x2＋5曲线的凸性，并确定其拐点.

习题13—6 设f（x）在[a，b]上强可导且导数f′（x）递增，求证：对任一点u∈[a，b]，当x≠u时有不等式f（x）＞f（u）＋f′（u）（x－u）.