牛顿采用的导数记号是在函数名上加个圆点.用一撇表示求导数运算，是拉格朗日首先采用的记法.

这个记号很方便，但有不足之处.例如，如果计算（uv）′，就有了问题：是把u看成自变量，还是把v看成自变量呢？把u看成自变量，v就是参数，uv就是幂函数，（uv）′＝v·uv－1；如果把v看成自变量，u就是参数，uv就是指数函数，则（uv）′＝uv·lnu；两者大不相同.

因此，如果用一撇表示求导数运算，就必须约定一个表示自变量的字母.这在讨论较复杂的问题时会带来不便.

微积分的另一位创建人莱布尼兹，对于求导的记号作了更细致的考虑，他建议用的求导记号，就是第6讲在强可导定义之后所介绍的，用或来表示函数y＝f（x）的导数.按照莱布尼兹的这种记号，＝v·，两者就分清楚了.

记号作为导数，本意是一个整体.但在引进微分的概念后，也可以看成两个微分的比.而且这样看带来很多方便.

什么是微分？在第3讲里提到过“微分三角形”，在第6讲里说过“通常把f（x＋h）－f（x）叫做函数f在x处的差分，通常记作Δy或者Δf（x）、Δf等；f′（x）h叫做f在x处的微分，通常记作dy或者df（x）、df等.”这样看，微分的意义很清楚也很简单，就是f′（x）h，这里h是不同于x的独立的变量.

既然dy＝f′（x）h，把x看成x自己的函数就有dx＝（x）′h＝h，于是dy＝f′（x）h＝f′（x）dx.这样，dy＝f′（x）dx就成为的另一种写法，即求微分的表达式.求微分的计算就是求导数的计算，只是用乘法形式代替了分数形式.这样一来，初等函数求导公式可以写成初等函数微分公式：

（1）常数：dC＝0；

（2）幂函数：dxn＝nxn－1dx（n非零整数，x∈（－∞，＋∞））；

dxα＝αxα－1dx（α非零实数，x＞0）.

（3）对数函数：dlnx＝（x＞0）；

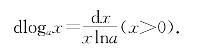
（4）指数函数：dex＝exdx；

dax＝axlnadx.

（5）三角函数：dsinx＝cos xdx

；

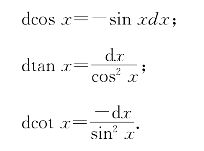（6）反三角函数：darcsinx＝；

darccosx＝；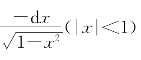

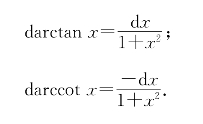
求导数的运算法则，也可以用微分等式来表示.记忆这些法则时，可以省略自变量x.

（i）函数线性组合的微分：d（αf＋βb）＝αdf＋βdg；

（ii）函数积的微分：d（f·g）＝fdg＋gdf；

（iii）函数商的微分：；

（iV）复合函数的微分：df（g）＝f′（g）dg；

（V）反函数的微分：若f（g（x））＝x，则dg＝.(www.daowen.com)

微分等式在表示复合函数的链式法则时更方便.设y＝f（u）且u＝g（x），按链式法则有dy＝df（g（x））＝f′（g（x））g′（x）dx；但由于u＝g（x），所以du＝g′（x）dx，这样就有dy＝df（g（x））＝f′（g（x））du，也就是dy＝df（u）＝f′（u）du，可见尽管u是中间变量，微分等式df（u）＝f′（u）du仍然成立.这样不论函数复合多少次，都可以按微分等式一层一层地计算.即所谓微分等式的不变性.

例题12—1 求复合函数y＝sineln（1＋x）2的微分.

解 记u＝ev，v＝lnw，w＝1＋x2；则

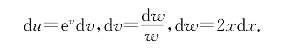
于是有　　　　　dy＝dsinu＝cosudu＝cosu·evdv

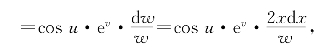
代换后得　

例题12—2 设曲线τ的方程为x2y＋xy2＋x2＋y2＝9，求曲线τ在点P（3，0）和Q（0，－3）处切线的斜率kp和kQ（图12－1）.

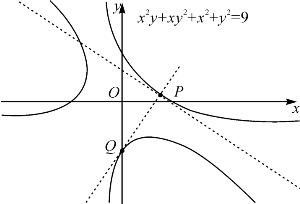
图12－1　曲线x2y＋xy2＋x2＋y2＝9及其切线

解 对曲线方程两端求微分得

x2dy＋2xydx＋2xydy＋y2dx＋2xdx＋2ydy＝0，

整理后为　　（x2＋2xy＋2y）dy＋（y2＋2xy＋2x）dx＝0，

因此有　

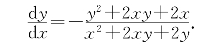
分别将P和Q的坐标代入得两点处切线斜率kp＝－和kQ＝.

习题12—1 求下列函数的微分：

（i）y＝）；

（ii）y＝.

习题12—2 设曲线τ的方程为x2＋（1＋sin2πx）y2＋xy＝3，求曲线τ在点P（1，1）和Q（0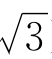，－）处切线的斜率kp和kQ（图12－2）.

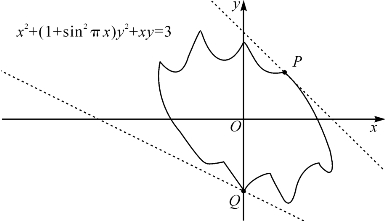
图12－2　曲线x2＋(1＋sin2πx)y2＋xy＝3及其切线