函数千千万万，最重要是哪些？数学中最重要也最常见的一大类函数是初等函数.所谓初等函数，是由不多的几种基本初等函数经过有限次四则运算和复合运算所得到的函数.基本初等函数共有6类，就是常数函数、幂函数、对数函数、指数函数、三角函数和反三角函数.这些函数的求导公式应当熟练掌握.

基本初等函数求导公式：

（1）常数C′＝0；

（2）幂函数（xn）′＝nxn－1　　（n非零整数，x∈（－∞，＋∞））；

（xα）′＝αxα－1　　（α非零实数，x＞0））.

（3）对数函数（lnx）′＝（x＞0）；（logax）′＝（x＞0）.

（4）指数函数（ex）′＝ex；（ax）′＝axlna.

（5）三角函数（sinx）′＝cosx；

（cosx）′＝－sinx；

（tanx）′＝；

（6）反三角函数（arcsinx）′＝（|x|＜1）；

从上面这些公式出发，应用计算导数的运算法则，就能根据初等函数的表达式求出其导数.计算导数的运算法则提炼后可以归结为下面五条：

（i）函数线性组合的导数：

（αf（x）＋βg（x））′＝αf′（x）＋βg′（x）；

（ii）函数积的导数：

（f（x）g（x））′＝f′（x）·g（x）＋g′（x）·f（x）；

（iii）函数商的导数：

（iV）复合函数的导数：(www.daowen.com)

（f（g（x）））′＝f′（g（x））g′（x）；

（V）反函数的导数：

若f（g（x））＝x则g′（x）＝　.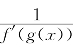

在应用这些法则求导时，所要求的条件简单说来有两条：一条是等式右端的求导运算可以进行，另一条是分母不为零.

上面不多的公式和法则，还可以再浓缩.

就法则而言，由于（αf（x））′＝αf′（x）是函数乘积公式的特殊情形，故（i）可以简化为函数和的求导法则即（f（x）＋g（x））′＝f′（x）＋g′（x）.函数积的求导法则，前面已经指出可以用取对数求导的方法导出.类似的，函数商的求导法则也可以用取对数求导的方法导出.也就是

整理即得.此外，反函数求导公式可以从复合函数求导的链式法则导出.

这样一来，求导法则中最基本的只有两条，就是函数和的求导法则和复合函数求导的链式法则.

至于基本初等函数的求导公式，则可以归结为三条：C′＝0，（lnx）′＝和（sinx）′＝cosx.

于是，初等函数的求导，归根结底就是两条求导法则和三个函数的导数公式.这五条要从定义出发推出来，其他的则可以从这五条推出来.

这样归纳虽欠严谨，但有助于从总体上理解把握.万一忘了或吃不准，就从这五条推一推.具体运用时，还是熟练掌握为好.

习题11—1 计算下列函数的导数：

习题11—2 填空

（i）（　　　）′＝3x2－x；

（ii）（　　　）′＝sin2x＋；

（iii）（　　　）′＝xex－；

（iV）（　　　）′＝lnx.