通常教材上首先引进指数函数，再将指数函数的反函数定义为对数函数.这里采用相反的次序，先引进对数函数，然后指出对数函数的反函数就是指数函数.这样做，对数函数的几何意义更直观，推理更简明.

由于当u≠v时lnu≠lnv，故y＝lnx有唯一的反函数，记作expx.称expx为以e为底的指数函数.显然expx和lnx互为反函数，两者的图象关于直线y＝x对称，如图10－1.

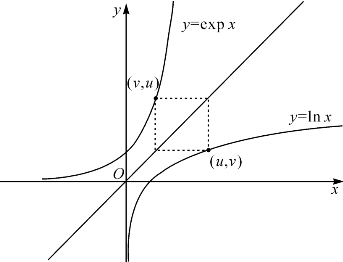
图10－1　自然对数函数lnx及其反函数expx的图象

命题10.1 （指数函数expx的性质）

（i）expx定义域为（－∞，＋∞），对一切x有expx＞0；

（ii）expx在（－∞，＋∞）上递增；

（iii）（加减变乘除）对任意两数A、B，有

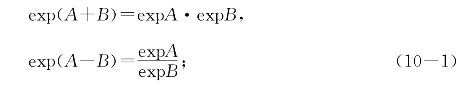
（iV）（乘除变乘开方）对任意正数A、整数n和非零整数m有

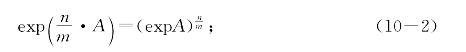
（V）

（Vi）expx差商有界.

证明 （i）由lnx定义域为（0，＋∞）可知对一切x有expx＞0：

由lnx无上下界可知expx定义域无上下界；

（ii）由lnx的递增性推出其反函数递增；

（iii）根据ln（AB）＝lnA＋lnB和反函数关系得

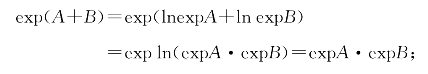
（iV）根据和反函数关系得

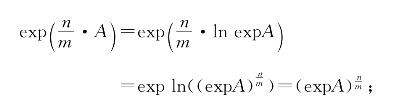
（V）由lne＝1得exp1＝explne＝e，再在（iV）中取A＝1即得；

（Vi）对任意的a＜b，有0＜A＝expa＜expb＝B，由不等式（9－2）即＜，在（0，＋∞）的任意闭子区间[A，B]上总有

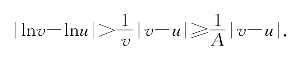
由命题5.4可知lnx的反函数在[a，b]上差商有界，从而expx在（－∞，＋∞）上差商有界.

命题证毕.

由上述结论（V）可见，expx就是以exp1＝e为底的指数函数.以后记expx＝ex.

对任意不为1的正数a，logax的反函数是什么呢？

如果f（x）是logax的反函数，按定义应当有

应用logax的定义得＝x，即lnf（x）＝x·lna.两端取指数函数值得exp（lnf（x））＝exp（x·lna），从而f（x）＝exp（x·lna）.这样就得到了logax的反函数exp（x·lna）.当x为有理数时，有

所以就记exp（x·lna）＝ax.即logax的反函数为ax.

由命题10.1容易推出函数exp（x·lna）＝ax的性质.

命题10.2 （指函数exp（x·lna）＝ax的性质）

（i）ax定义域为（－∞，＋∞），对一切x有ax＞0；

（ii）ax在（－∞，＋∞）上当a＞1时递增，a＜1时递减；

（iii）（加减变乘除）对任意两实数u、v，有

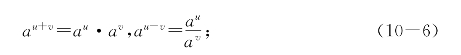
（iV）（乘除变乘开方）对任意两实数u、v，有

（V）a0＝1，a1＝a.　　　　　　　（10－8）

命题10.2的证明留给读者.图10－2是不同底的几个指数函数的图象.

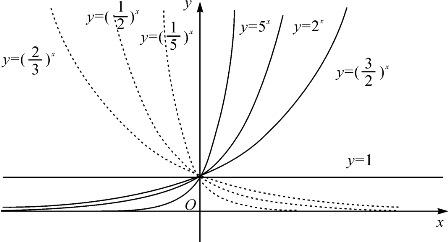
图10－2　不同底的几个指数函数的图象

下面讨论指数函数的求导问题.

在估值不等式中取u＝ex和v＝ey，得到

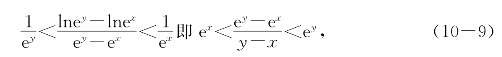
这表明函数y＝ex自己是自己的乙函数，由y＝ex差商有界，从而得到

命题10.3 指数函数求导公式

这是微积分中最美的事实之一，(www.daowen.com)

根据exp（x·lna）＝ax，改写符号得exp（a·lnx）＝xa，这里x＞0而a为任意非零实数.从而得

命题10.4 一般幂函数求导公式

证明 应用链式法则得

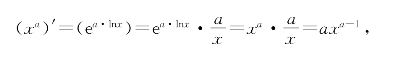
证毕.

回头分析一下推导指数函数导数公式的过程，从中可以找出反函数一般求导方法.

命题10.5 设F（x）在[a，b]上强可导且对任意x∈[a，b]有F′（x）≠0.则其反函数G（x）强可导且有

此命题涉及反函数存在性，其证明放在第18讲中（命题18.5）.为了加深对这个公式的印象，可以对反函数的定义等式F（G（x））＝x两端求导，由链式法则得F′（G（x））·G′（x）＝1，这样自然得到了（10－12）.

从几何上看，如图10－3.F（x）的图象和G（x）的图象关于直线L：y＝x对称，曲线y＝G（x）上的点P＝（u，v）和曲线y＝F（x）上的点Q＝（v，u）对称，两点处的切线也对称，从而其切线斜率互为倒数.

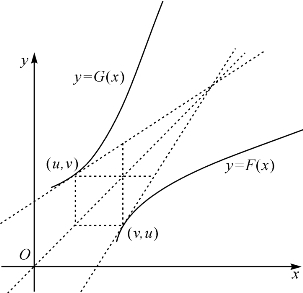
图10－3　反函数导数的几何意义

除了对数函数和指数函数互为反函数外，重要的反函数的例子是反三角函数，主要是反正弦函数、反余弦函数、反正切函数和反余切函数.

由于三角函数的周期性，必须限制其定义域在某个范围内才有唯一的反函数，为方便，约定将sinx的定义域限定在以确定其反函数arcsinx.也就是说，函数arcsinx定义于[－1，1]而取值于，满足条件sin（arcsinx）＝x.类似的，将cosx的定义域限定在[0，π]以确定其反函数arccosx.将tanx的定义域限定在以确定其反函数arctanx，将cotx的定义域限定在[0，π]以确定其反函数arccotx.这几个函数的图象如图10－4至图10－7.

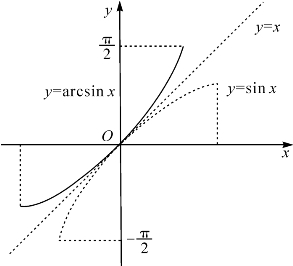
图10－4　反三角函数arcsinx的图象

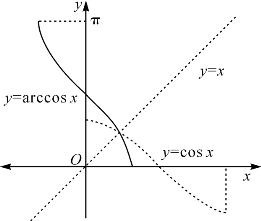
图10－5　反三角函数arccosx的图象

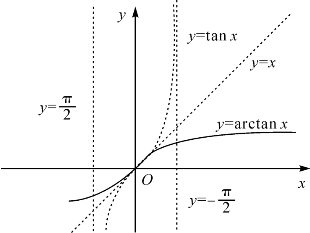
图10－6　反三角函数arctanx的图象

图10－7　反三角函数arccotx的图象

例题10—1 计算反三角函数arcsinx和arctanx的导数.

解 （i）由sin（arcsinx）＝x两端求导数得cos（arcsinx）·（arcsinx）′＝1，

再应用cosA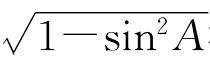＝得

从而有

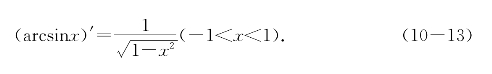
（ii）直接应用反函数求导公式（命题10.5）和（tanx）′＝，以及三角恒等式得

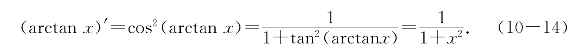
例题10—2 计算y＝ax的导数（a＞0）.

解 由ax＝exlna，用链式法则得

例题10—3 计算xx的导数（x＞0）.

解 将xx取自然对数得x·lnx，故xx＝exlnx.用链式法则得

例题10—4 求证：当h≠0时有

解 当h＞0时在不等式（10－9）即中取y＝h和x＝0得1＜，乘以h得h＜eh－1＜h·eh；

当h＜0时取y＝0和x＝h得，乘以h得h·eh＞eh－1＞h.结论获证.

习题10—1 求下列函数的导数：

（i）x2ex；

（ii）2x（sinx＋cosx）；

（iii）ln ；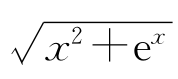

（iV）（1＋x4）cosx.

习题10—2 计算反三角函数arccosx和arccotx的导数.

习题10—3 试证明对任意闭区间[a，b]上的x和x＋h有不等式

|ex＋h－ex－hex|＜h2eb.

习题10—4 试讨论函数y＝axlna－lnx的零点个数和a的关系.