到现在为止，还没有讲指数函数和对数函数的求导方法.

如果按照中学教材上的办法引进指数函数和对数函数，这两类函数的求导公式很难推导.这里将采用另一种直观严谨而且简单的方法引进对数和指数函数并导出其求导公式.

这种方法的基点，是考虑反比例函数曲线下的曲边梯形面积.

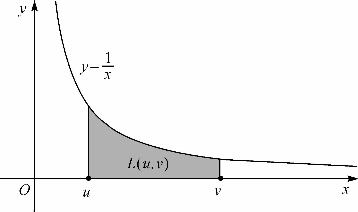
图9－1　反比函数曲线下的面积

定义6 （自然对数）对于任意两正数0＜u＜v，记区间[u，v]上反比例函数y＝曲线下的曲边梯形面积（图9－1）为L（u，v），并约定L（u，v）＝0和L（v，u）＝－L（u，v）.记lnx＝L（1，x）.这样，就在（0，＋∞）上定义了一个函数y＝lnx，lnx叫做x的自然对数（图9－2）.

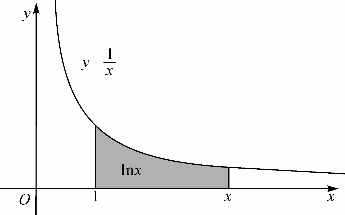
图9－2　自然对数lnx的定义

由定义和面积性质容易检验对任意3个正数x、y、z有

从而可知lnv－lnu＝L（u，v），且当u＜v时它就是y＝曲线下在区间[u，v]上的面积（图9－3），从而得到下面的重要命题，

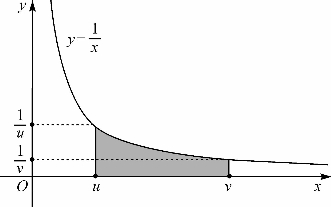
图9－3　表示lnv－lnu的一块面积

命题9.1 （自然对数函数的基本不等式和求导公式）

（i）对任意0＜u＜v有不等式

（ii）函数lnx在（0，＋∞）上强可导，其导数为反比例函数：

证明 （i）图9－3中阴影部分的面积就是lnv－lnu＝L（u，v），显然有

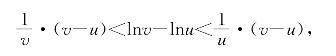
同除以（v－u）得（9－2）；

（ii）不等式（9－2）表明y＝是函数y＝lnx的乙函数.由例题5－3知y＝在（0，＋∞）上差商有界，由命题6.4推出y＝lnx在（0，＋∞）上强可导，且有（lnx）′＝.证毕.

函数y＝lnx的图象见图9－4.

图9－4　函数y＝lnx的图象

命题9.2 （自然对数函数y＝lnx的性质）

（i）（递增性）y＝lnx在（0，＋∞）上有定义且单调递增；

（ii）（正负区间）ln1＝0，当0＜x＜1时lnx＜0，当x＞1时lnx＞0；

（iii）（乘除变加减）对任意正数A和B，有

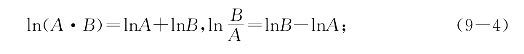
（iV）（乘开方变乘除）对任意正数A、整数n和非零整数m，有

（V）（无界性）lnx无上界也无下界.

证明 （i）由（lnx）′＝＞0可知lnx递增；

也可用不等式（9－2）更直接地证明；

（ii）递增性和ln1＝0可得x＜1时lnx＜0，x＞1时lnx＞0；

（iii）对任意正数A和x，由链式法则得（lnAx）′＝，于是

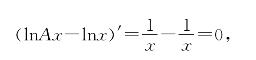
可见对任意的x都有lnAx－lnx＝C.取x＝1得C＝lnA，再取x＝B得ln（A·B）＝lnA＋lnB；这推出

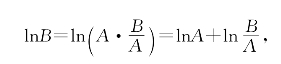
即（9－4）的另一式ln＝lnB－lnA；

（iV）用链式法则得到

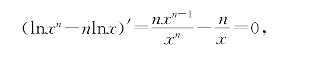
可见对任意的x都有lnxn－nlnx＝C.取x＝1可以确定C＝0，故得lnxn＝nlnx，从而取x＝A得

即·lnA；

（V）对任意的A＞0，当n＞时有nln2＞A即ln2n＞A，可见lnx没有上界；同时有－nln2＜－A即ln0.5n＜－A，可见lnx没有下界.

命题9.2证毕.

有了自然对数，就容易定义和研究一般的对数了.(www.daowen.com)

定义7 设a是不等于1的正数，记＝logax，称logax为x的以a为底的对数；特别地记lgx＝log10x，称为常用对数.

命题9.3 （一般对数函数y＝logax的性质）

（i）（增减性）y＝logax在（0，＋∞）上有定义，且当a＞1时单调递增，当a＜1时单调递减；

（ii）（正负区间）loga1＝0，当a＞1时logax在（0，1）上为负而在（1，＋∞）上为正，当a＜1时logax在（0，1）上为正而在（1，＋∞）上为负；

（iii）（乘除变加减）对任意正数A和B，对不为1的正数a有

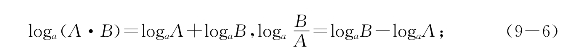
（iV）（乘开方变乘除）对任意正数A、整数n和非零整数m，对不为1的正数a有

（V）（无界性）logax无上界也无下界；

（Vi）对不为1的正数a有logaa＝1和loga1＝0.

命题9.3的证明可以由logax的定义和命题9.2推出.详细推导留给读者.

自然会问，lnx是不是logax中之一呢？如果是，底是什么数？

按定义，如果有一个实数e使得logax＝lnx，则lnx＝logex＝，立刻推出lne＝1.因此，自然对数就是以e为底的对数.

这个实数e是多大呢？在（9－2）即中取v＝2和u＝1得到0.5＜ln2＜1，而ln4＝ln22＝2ln2＞1，可见应有e∈（2，4）.更精密的估计为e＝2.718281828459……，深入研究后可知它是一个无理数.这是数学中除π之外最重要的无理数.由lnx的定义可知，在曲线y＝下区间[1，e]上的面积为1.这就是自然对数的底之几何意义.

函数y＝logax的图象如图9－5.

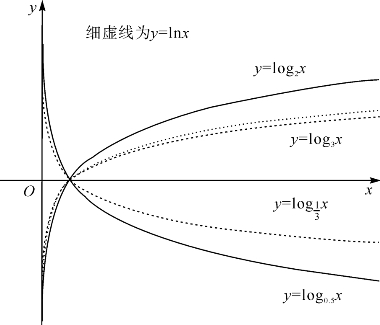
图9－5　函数y＝logax的图象

例题9—1 求证＜ln（1＋x）＜x. （9－8）

证明 当x＞0时，在不等式（9－2）即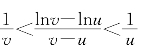中取u＝1而v＝1＋x可得＜1，两端乘x得不等式（9－8）；当－1＜x＜0时，在同一不等式中取u＝1＋x而v＝1可得，两端乘x时不等式反号，仍得不等式（9－8）.证毕.

图9－6直观地说明了不等式（9－8）.

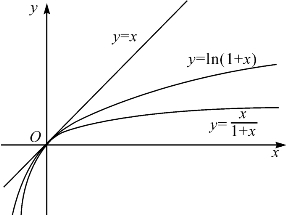
图9－6　函数ln(1＋x)的估计

例题9—2 （换底公式）设a和b都是不为1的正数，求证：logax＝logab·logbx.　　（9－9）

证明 根据定义7，有

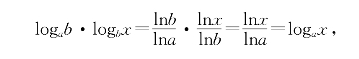
即所欲证.

例题9—3 求函数y＝ln|x|在（－∞，0）∪（0，＋∞）上的导数.

解 已知在（0，＋∞）上有（ln|x|）′＝（lnx）′＝.当x∈（－∞，0）时由链式法则得

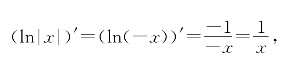
故有一般公式　

例题9—4 （取对数求导法）已知f（x）、g（x）、h（x）都在I上强可导且不为0，令w（x）＝f（x）·g（x）·h（x），求w（x）的导数.

解 对等式

求导数得　

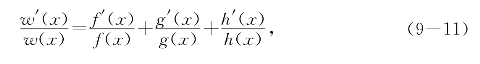
去分母得

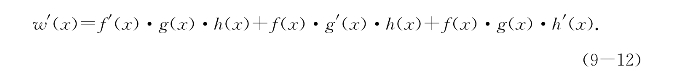
这样比使用乘积求导公式有时方便一些.

习题9—1 设n为正整数.试证明：

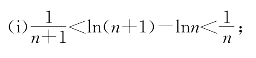
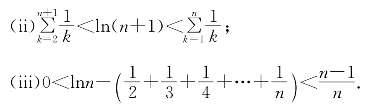
习题9—2 设a、b和c都是不为1的正数，问logab·logbc·logca＝？

习题9—3 求下列函数的导数

（i）x2lnx；

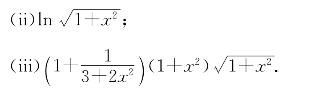
习题9—4 求证：当0＜a＜x＜x＋h时有.