从第1讲开始，我们就知道了几个函数的导数计算公式，接下来我们知道，这几个函数的导数也都是乙函数，而且差商有界；更进一步知道，差商有界的乙函数都是强导数.利用乙函数和强导数的定义，我们用严谨清楚的不等式代替了直观但一时还说不清的极限概念，并且进一步求出了xn和sinx的导数（而且是强导数）.运用这些函数的导数，解决了一批原本看起来比较困难的问题：求曲线的切线、求函数的最值、估计某些函数的数值等.

为了更广泛地应用导数知识，就要知道更多函数的求导公式.根据定义一个函数一个函数地推导，显然是个笨办法.开始用笨办法求几个函数的导数，是必要的.进一步，应当在此基础上提升，扩大战果.

其实，前面也用了扩大战果的思想.利用命题2.3和乙函数与强导数的关系，如果知道了f（x）的强导数，就能求出f（x）＋k·x＋C的强导数和f（k·x＋C）的强导数：

（f（x）＋k·x＋C）′＝f′（x）＋k；

（f（k·x＋C））′＝k·f′（k·x＋C）.

注意上面后一个等式中求导记号的写法：表达式括弧外的一撇（f（k·x＋C））′，表示先将k·x＋C代入f（x）再求导；而函数名上的一撇f′（k·x＋C），则表示先求导再把k·x＋C代入.例如设f（x）＝x2，则

显然两者有所不同，前者多一个常数因子k.

有了这样的公式，在计算函数f（x）＝（3x＋2）13的导数时，就不必展开.直接用公式得到f′（x）＝（（3x＋2）13）′＝3·13（3x＋2）12＝39（3x＋2）12.这就是扩大战果的好处.

由此自然联想到要问，知道了f（x）和g（x）的导数，能不能据此计算出两个函数的和、差、积、商的导数？

下面的几个命题，圆满地实现了这个扩大战果的设想.

命题7.1 （函数和的求导法）若f（x）和g（x）都在区间I上强可导，则函数f（x）＋g（x）也在区间I上强可导，且有

证明 根据强可导的定义和题设，对于任意闭区间[a，b]⊆I，有正数M1和M2使对[a，b]中任意的x和x＋h有下列不等式成立

两式相加，记H（x）＝f（x）＋g（x），得

记M1＋M2＝M，可将上式写成

由定义可知f′（x）＋g′（x）在I上是H（x）＝f（x）＋g（x）的强导数.

由于－g（x）显然强可导且有（－g（x））′＝－g′（x），故可知f′（x）－g′（x）在I上是f（x）－g（x）的强导数.

有了上面的命题，所有多项式函数的导数都容易计算了.

命题7.2 （函数积的求导法）若f（x）和g（x）都在区间I上强可导，则函数f（x）·g（x）也在区间I上强可导，且有

证明 根据强可导的定义和题设，对于任意闭区间[a，b]⊆I，有正数M1和M2使对[a，b]中任意的x和x＋h有不等式（7－2）和（7－3）成立.记

则有

此外，由命题6.2可知有正数A使对[a，b]中任意x和x＋h有

将（7－7）和（7－8）移项得

两式相乘得

记H（x）＝f（x）g（x），由（7－13）移项再用不等式（7－9）和（7－10）得

|H（x＋h）－H（x）－（f（x）g′（x）－g（x）f′（x））h|

＝|f′（x）g′（x）h2＋R1g（x＋h）＋R2f（x＋h）－R1R2|

≤|f′（x）g′（x）h2|＋|R1g（x＋h）|＋|R2f（x＋h）|＋|R1R2|

＜A2h2＋M1Ah2＋M2Ah2＋M1M2h4

根据强导数的定义，（7－14）表明f（x）g′（x）＋g（x）f′（x）是函数H（x）＝f（x）g（x）在[a，b]上的强导数，因[a，b]是I的任意闭子区间，故它也是H（x）＝f（x）g（x）在I上的强导数，即所欲证.

有了函数之积的求导公式，容易从一些简单的等式导出新的等式甚至求导公式.

例题7—1 求函数f（x）＝x2sinx的导数.

解 f′（x）＝（x2sinx）′＝x2·（sinx）′＋（x2）′·sinx＝x2cosx＋2xsinx.

例题7—2 试从（x）′＝1出发推导xn（n为正整数）的求导公式.

解 用函数积求导公式可得

（x2）′＝（x·x）′＝x′·x＋x′·x＝x＋x＝2x，

（x3）′＝（x2·x）′＝（x2）′·x＋x′·x2＝2x2＋x2＝3x2，

（x4）′＝（x3·x）′＝（x3）′·x＋x′·x3＝3x3＋x3＝4x3，(www.daowen.com)

……

由此猜想有一般公式（xn）′＝nxn－1.对n作数学归纳.若对n＝k＞1有（xk）′＝k·xk－1，则有

（xk＋1）′＝（xk·x）′＝（xk）′·x＋x′·xk＝k·xk＋xk＝（k＋1）xk，

这证明了一般公式（xn）′＝nxn－1成立.

回顾一下，是不是比按定义直接求要方便？

例题7—3 根据（sinx）′＝cosx，猜想的表达式.

解 将等式sinx·两端求导数得

即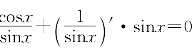，解得.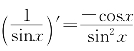

利用函数乘积的求导公式，容易从形式上导出两函数之商的求导公式.这只要对等式·f（x）＝g（x）两端求导，得到

由（7－15）解出，便可以猜想到两函数之商的求导公式：

命题7.3 （函数商的求导法）若f（x）和g（x）都在区间I上强可导且对任意x∈I有f（x）≠0，则在区间I上强可导且

这样从函数积的求导公式引出函数商的求导公式，要假定商函数强可导.虽缺严谨推导，但便于记忆.微积分的不少定理公式，都是人们先直观地看出来或大致地算出来，然后再严谨求证的.学习微积分，也要学这样的似然推理，这样有利于把知识联系起来，不但便于记忆，也能启发创新思维.

应当说明，在中学课程里不要求严谨证明这些求导公式，只要记住并会用就可以了.

在（7－16）中取g（x）＝1，便得到函数的倒数的求导公式.反过来，如果先知道了函数的倒数的求导公式，应用函数乘积的求导公式就能推出函数商的求导公式.下面的命题证明了闭区间上函数倒数的导数公式，为证明函数商的求导公式提供了基础.

命题7.4 （闭区间上函数倒数的求导法）设f（x）在区间[a，b]上强可导，且有正数B使得对任意x∈[a，b]有|f（x）|≥B；则在[a，b]上强可导且

证明 记R＝f（x＋h）－f（x）－f′（x）h.由题设条件和强导数定义以及命题6.2，可知有正数M1和A使得对[a，b]上的任意两点x和x＋h有诸不等式

从而有

记N＝M1|b－a|＋A，于是得

这里记M＝，则不等式（7－20）的两端表明在[a，b]上的强导数是，故（7－17）成立.即所欲证.

细心的读者会注意到，在命题7.4中要求|f（x）|在[a，b]上有正的下界B，而在命题7.3中的条件仅仅是f（x）≠0.这就有一个问题：在闭区间上的差商有界的正值函数是否一定有正的下界？这个问题将在第18讲中回答（命题18.4的推论2）.

例题7—4 求证正切函数tanx在其定义域上强可导，且有

解 应用命题7.3得

习题7—1 求下列函数的导数：

（i）f（x）＝x100－5x4＋3x3－x2＋x＋88；

（ii）f（x）＝（x5－1）（x10－x5＋1）；

（iii）f（x）＝x2sinx＋2xcosx－2sinx；

（iV）g（x）＝sin2（x2＋1）＋cos2（x2＋1）；

（V）g（x）＝；

（Vi）f（x）＝.

习题7—2 试从两函数之积的求导公式，推导三个函数之积的求导公式.

（f（x）g（x）h（x））′＝f′（x）g（x）h（x）＋f（x）g′（x）h（x）＋f（x）g（x）h′（x）.

习题7—3 试推导余切函数求导公式.

习题7—4 对下列等式两端求导数，看看得到什么.

（i）sin2x＝2sinx·cosx；

（ii）tan（x＋a）＝.