第1讲引进了函数的导数，第2讲引进了函数的乙函数.一个一个比较两讲中的命题，会引起一个猜想，乙函数就是导数吧？

导数的概念，从一开始就和神秘莫测的无穷小结下不解之缘；而乙函数的引入，却如此平凡普通，两者怎么可能是一回事儿？

现在真相即将浮出水面.借助于“差商有界”的概念，乙函数和导数之间的关系就要明朗化了.

命题6.1 设函数g（x）是f（x）在[a，b]上的乙函数；如果g（x）在[a，b]上差商有界且M是其李普西兹常数，则对[a，b]中任意两点u＜v和s∈[u，v]有

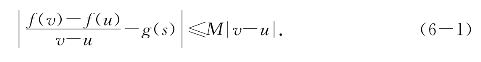
或者等价地

证明 由乙函数定义，有[u，v]上的点p和q使g（p）≤≤g（q），同减g（s）得

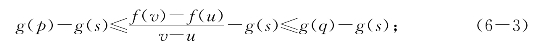
再由g（x）在[a，b]上差商有界且M是其李普西兹常数得

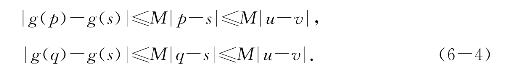
将（6－4）用于（6－3），即得（6－1）；去分母得（6－2）.证毕.

不等式（6－1）表明，在命题条件下f（x）在[u，v]上的平均变化率可以取g（x）在[u，v]上的任一点s处的值作为近似值.其误差不超过M|v－u|.这比乙函数定义中的估值不等式更具体.

再仔细看看不等式（6－1），你发现了什么？

注意s是[u，v]上的任意一点，所以可令s＝u；再记v－u＝h，于是v＝u＋h，（6－1）就成了

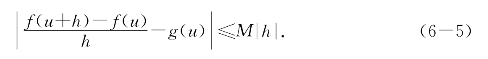
不等式（6－5）就是林群提出的简化的导数定义.

在上面这个不等式中，如果h无限地趋于0，右边的M|h|也就无限地趋于0，从而差商和一个确定的数A＝g（u）无限接近.按定义1，g（u）就是函数f（x）在点x＝u处的导数！f′（u）＝g（u）！

真相大白，水落石出.原来差商有界的乙函数就是导数.

反过来，导数是否一定是差商有界的乙函数呢？

这可不一定.观察（6－5），如果把右端的M|h|换成M 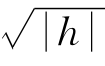，让h无限地趋于0，右边的M 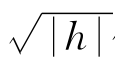仍然无限地趋于0，g（u）仍是函数f（x）在点x＝u处的导数！

对任意正整数n＞1，把M|h|换成M 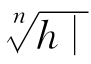，仍然推出g（u）是函数f（x）在点x＝u处的导数.条条大路通罗马.

因此，（6－5）是f′（u）＝g（u）的充分条件，而不是必要条件.为区别（6－5）和f′（u）＝g（u），我们给出下面的定义.

定义5 （强可导函数的导数）设函数f（x）和g（x）在[a，b]上有定义.如果有数M使对[a，b]上任两点x和x＋h成立不等式

或等价的

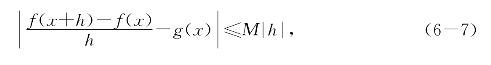
则称函数y＝f（x）在[a，b]上强可导；若f（x）在区间I的任意闭子区间都是强可导的，则称其在I上强可导.称g（x）是f（x）是强导数.

如上所述，强导数也是导数，故同样记作f′（x）＝g（x）或y′＝g（x），也可记作或等.在国外一些大学的微积分教材中，强可导叫做李普西兹可导，强可导函数的导数叫做李普西兹导数.

同样是定义导数，定义5比定义1清楚.定义1中用到一些直观的描述，有待在将来严谨化.定义5则是明明白白的不等式.

不等式（6－7）的意义比较清楚：f（x）的导数f′（x）＝g（x）是差商的近似值，对于强导数而言，误差不超过M|h|.

去分母之后的（6－6）即|f（x＋h）－f（x）－f′（x）h|≤Mh2，又有什么意义呢？

通常把f（x＋h）－f（x）叫做函数f在x处的差分，通常记作Δy或者Δf（x）、Δf等；f′（x）h叫做f在x处的微分，通常记作dy或者df（x）、df等.（6－6）表明当h接近于0时，差分与微分之差比h更接近于0，对于强导数而言，此差不超过Mh2.

在第3讲里提出了曲线切线的独立的定义，即定义3.为了说明函数的导数是其曲线的切线斜率，按该定义需要证明一个不等式d（B，AP）＞d（B，AQ）（见（3－4）和（3－5）及其上下文）.现在有了强可导的概念，可以把这个问题说清楚了！

为了阅读方便，下面重复一段第3讲的文字和一幅图的内容.

设函数f（x）在[a，b]上强可导，而u∈（a，b）.如图3－6，点A＝（u，f（u））在函数y＝f（x）的曲线上.

要证明在点A附近最接近曲线y＝f（x）的是图中直线AQ：y＝f′（u）（x－u）＋f（u）.另一条直线AP为y＝k（x－u）＋f（u），k≠f′（u）.

设B＝（v，f（v））是曲线y＝f（x）上另一点，如图，分别计算它到AQ和AP的距离.记h＝v－u≠0，可得

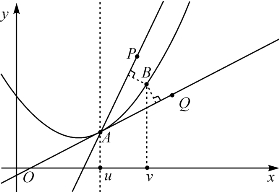
复制图3－6　曲线上一点到两直线距离的比较

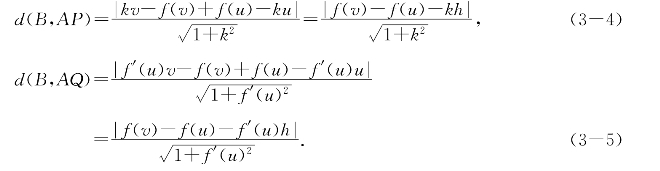
要证明的是，当|h|＞0足够小时有d（B，AP）＞d（B，AQ）.

设u和v都在[a，b]上，根据强可导函数的定义，有正数M使得

|f（v）－f（u）－f′（u）h|≤Mh2，

故由（3－5）得d（B，AQ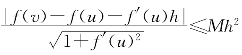）＝，而由（3－4）则有

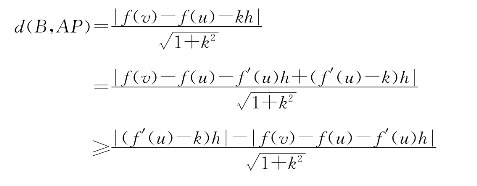
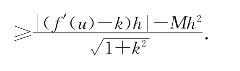
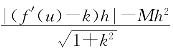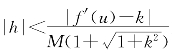于是为了使d（B，AP）＞d（B，AQ），只要＞Mh2即可.这只要|f′（u）－k|＞M|h|（1＋），即就可以了.

至此，对于强可导函数，我们严谨地论证了导数确实是函数曲线上的切线的斜率.

由于导数f′（x）是函数f的曲线在x处的切线的斜率，所以差分和微分的关系如图6－1.图中AD＝h，切线AC的斜率为f′（x），故DC＝f′（x）h是f（x）的微分，而BD＝f（x＋h）－f（x）为差分.两者之差BC当AD＝h很小时比h更小，即不但BC很小，比值也很小.

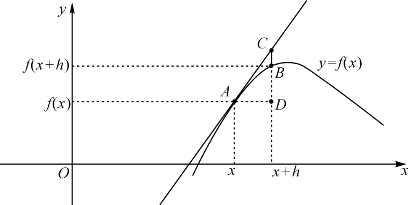
图6－1　当h很小时微分和差分的差更小

由命题6.1和定义5，差商有界的乙函数不但是导数，而且是强导数，如果f（x）有差商有界的乙函数，则它是强可导的.

回顾第1讲计算的几个函数的导数，即第2讲里举出的乙函数，它们都是差商有界函数，所以无一例外都是李普西兹导数.事实上，想找一个可导但不是强可导的函数是相当不容易的.在高等数学教材的习题或试卷上出现的函数，99%以上是强可导的.

数学中讨论问题，常常要考虑正反两个方面，知道了差商有界的乙函数是强导数，自然要问反过来如何.

命题6.2 （强导数和强可导函数的差商有界性和有界性）设在区间I上g（x）是f（x）的强导数，则有

（i）g（x）和f（x）都在I上差商有界；

（ii）对于任意的[a，b]∈I，g（x）和f（x）都在[a，b]上有界.

证明 关键在于证明g（x）在I上差商有界.

（i）根据定义5.对[a，b]∈I有正数M使对[a，b]上任两点u和v＝u＋h成立不等式

交换u和v的位置得

两式相加得

于是有|g（v）－g（u）|≤2M|v－u|，可见g（x）在I的任意闭子区间上差商有界，即在I上差商有界.

由命题5.1，g（x）在I的任意闭子区间[a，b]上有界，即有正数M1使对任意x∈[a，b]有|g（x）|＜M1.

于是由强导数定义可知有正数M2，使对[a，b]上任意两点u和v有不等式

从而得

这证明了f（x）在[a，b]上差商有界.由于[a，b]是I的任意闭子区间，故f（x）在I上差商有界.

（ii）由命题5.1，由f（x）在[a，b]上差商有界知f（x）在[a，b]上有界，另上面已经证明有正数M1使对任意x∈[a，b]有|g（x）|＜M1，即得所要的结论.

进一步问，强导数是否一定也是乙函数呢？下面作出了肯定的回答.

命题6.3 （估值定理）设f（x）在I上强可导，f′（x）＝g（x），则g（x）是f（x）在I上的乙函数.即对任意[u，v]⊆I，有[u，v]中的两点p和q满足

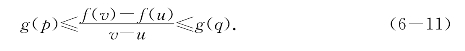
证明 若对于所有x∈（u，v]差商为常数，结论显然.如不然，必有[r，s]⊂[u，v]使得

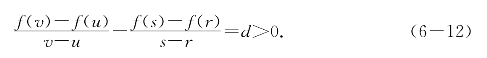
由强可导定义，有正数M使对一切x∈[u，v]和（x＋h）∈[u，v]有

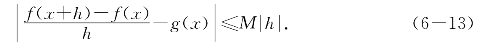
取正整数n＞，将[r，s]等分为n段，记h＝，则Mh＜d；且n段中必有一段[p，p＋h]使得不等式

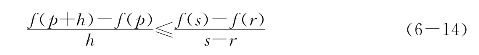
成立.由（6－13）、（6－14）和Mh＜d以及（6－12）得(www.daowen.com)

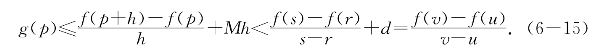
为了证明结论的另一半，可设G（x）＝－f（x），则G′（x）＝－g（x）.对G（x）应用上面得到的结论，可知有q∈[u，v]满足

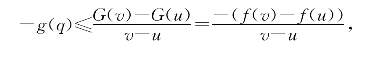
即满足≤g（q）.命题证毕.

射人先射马，擒贼先擒王.理解数学证明，要抓主干思想.命题6.3的证明好像环节较多，又是中学生不很熟悉的不等式，仅仅循章索句来读，必有困难.若先理清其思路，则有高屋建瓴之效果.命题要求找两点p和q使g（p）和g（q）能够把差商夹在中间.设想若f（x）在[u，v]上不是均匀变化，把[u，v]分成多个小段时，其中必有两小段上的差商能够把差商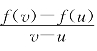夹在中间.根据强可导定义，小段上的差商和该段端点处的强导数g（x）的值很接近，于是用g（x）的值代替小段上的差商就可以完成证明.具体的不等式推演，不过是上述思想的实现而已.

命题6.3在微积分中的作用，相当于传统微积分教程中的拉格朗日中值定理，所以命名为“估值定理”与之对应.拉格朗日中值定理的成立依赖于实数理论，其证明又涉及极限概念和闭区间上连续函数的性质，推理迂回繁琐.我们仅仅对函数类加上差商有界的限制，就减少了很多麻烦，确实合算.而且如果略为深入探索，差商有界的限制还可以大大放宽，这是后话.

将上面三命题集成，得到想要的结论：

命题6.4 g（x）在区间I上为f（x）的强导数的充要条件，是g（x）在区间I上差商有界且为f（x）的乙函数.

这样一来，前面所述有关乙函数的性质、乙函数的运算、乙函数的应用，都可以适用于强导数.另一方面，验证一下强导数定义中的不等式（6－6）或（6－7），就一箭双雕地确认了g（x）既差商有界又是f（x）的乙函数.

对许多函数，验证不等式（6－6）或（6－7）并不难.举几个例子.

例题6—1 求证g（x）＝2x是函数f（x）＝x2的强导数

证明1 计算差商得

故有　

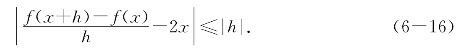
由定义知2x是x2的强导数.

证明2 因2x是x2的差商有界的乙函数，故是x2的强导数.

如图6－2，y＝x2表示边长为x的正方形的面积.如果x增大成为x＋h，则正方形面积增加的部分，即差分（x＋h）2－x2＝2xh＋h2；它由2个面积为xh的长条矩形和一个面积为h2的小正方形组成.微分则为2xh，舍弃了面积为h2的小正方形.

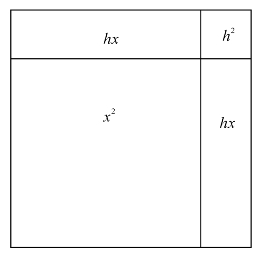
图6－2　正方形面积的增加部分

例题6—2 求函数f（x）＝x3的强导数.

解1 函数f（x）＝x3的差商为

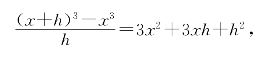
在任意区间[a，b]上有不等式

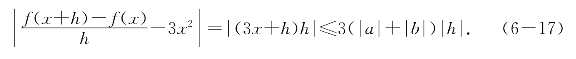
由定义得f（x）＝x3强可导且f′（x）＝（x3）′＝3x2.

解2 因3x2是x3的差商有界的乙函数，故是x3的强导数.

例题6—3 求F（x）＝（x≠0）的强导数.

解1 对于不含0的闭区间[a，b]中的x和x＋h计算差商得

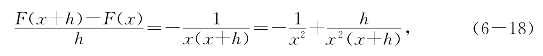
移项，并且设m＝min{|a|，|b|}，则有

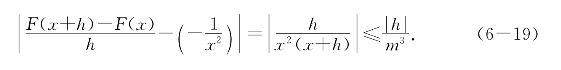
由定义得－是的强导数.

解2 因－是的差商有界的乙函数，故是的强导数.

例题6—4 求证是函数G（x）＝（x＞0）的强导数.

解1 设0＜a＜b，在[a，b]上估计函数的差商和的差得

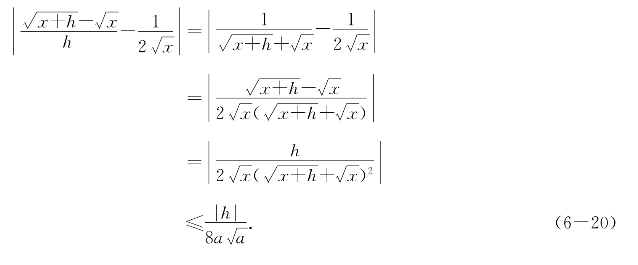
由定义得知是的强导数.

将（6－20）写成形式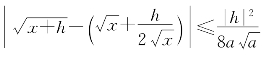，可以看出的近似值为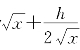而误差不超过，这里a可取x和x＋h中较小者.例如，…，误差不超过.这比例题1－2和2－2更为直截了当.

解2 因是的差商有界的乙函数，故是的强导数.

下面涉及一些新的求导公式，不再作为例题，升格为命题.

命题6.5 求正整数n，函数g（x）＝nxn－1是f（x）＝xn的强导数.

证明 由

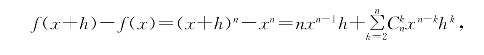
当x∈[a，b]时得

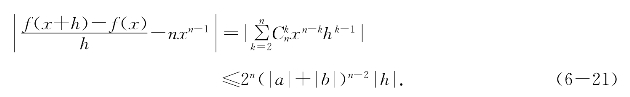
由定义可知f（x）＝xn强可导且

f′（x）＝（xn）′＝nxn－1.

顺便得知g（x）＝nxn－1是f（x）＝xn的差商有界的乙函数.

命题6.6 函数cosx是sinx的强导数，－sinx是cosx的强导数.

证明 前面已经证明cosx差商有界，下面再证明cosx是sinx的乙函数，就推出cosx是sinx的强导数.

对任意整数k和[kπ，（k＋1）π]上的两点u＜v＝u＋2h，有：

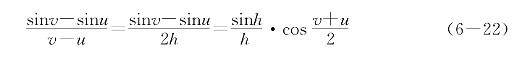
注意当0＜h＜时有sinh＜h＜tanh（参看图5－2），从而0＜h≤时有0≤cosh＜＜1；于是（6－22）的左端在cos和

之间.注意cosx在[kπ，（k＋1）π]单调，故都在cosu和cosv之间，这表明，在[kπ，（k＋1）π]上cosx是sinx的乙函数.从而在（－∞，＋∞）上cosx也是sinx的乙函数，应用命题2.3可知是sin的强导数.证毕.

直观地看，cosx是sinx的乙函数可以用几何图形清楚地说明.如图6－3，设u＜v＜π且u＋v＜π，作腰长AC＝BC＝1且顶角∠ACB＝v－u＝2h的等腰三角形ABC；延长BA至D使得∠ACD＝u，记CD＝b；作三角形ABC的高CE；以C为心AC为半径作弧AB，则其长度α＝2h，；以C为心AE为半径作弧PQ，则扇形PQC面积为σ＝CE2h；作三角形ACD的高DF、ECD的高EG和BCD的高BH；记三角形ABC的面积为ΔABC，则有

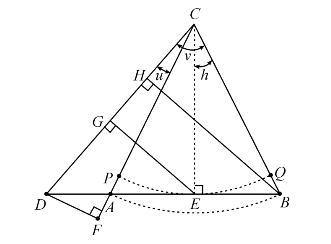
图6－3　从几何上看cosx是sinx的乙函数

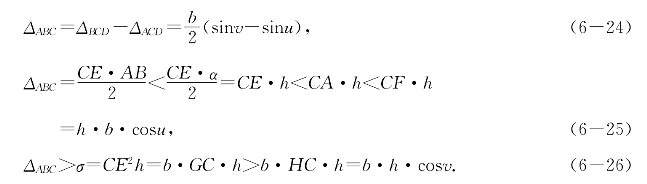
（关于不等式（6－26），图上画出的是v为锐角情形，非锐角情形显然成立.）于是得

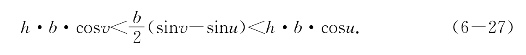
同除以hb，注意2h＝v－u便得

这样推理清清楚楚，而且不用先预备好关于正弦的不等式.

在（6－28）中取u＝x和v＝x＋h，移项去分母得

这表明sinx＋hcosx是sin（x＋h）的近似值，误差不超过h2.

例题6—5 应用（6－29）求sin31°的近似值.

解 在（6－29）中取x＝30°＝和h＝1°＝≈0.017453，得到

sin31°≈sin30°＋0.017453cos30°＝0.5＋0.017453×≈0.5151，

误差不超过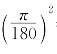≈0.0003.

习题6—1 求函数f（x）＝x2＋的强导数.

习题6—2 求函数f（x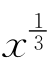）＝的强导数.

习题6—3 求F（x）＝x4＋3x3＋3x2＋x的强导数.

习题6—4 求函数G（x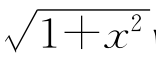）＝的强导数.

习题6—5 求证对负整数n，函数g（x）＝nxn－1（x≠0）是f（x）＝xn的强导数.

习题6—6 如图6－4，在单位圆O上取A、B、C使得∠BOA＝u和∠COA＝v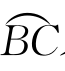，表示弧长.

求证：cosv＜＜cosu.

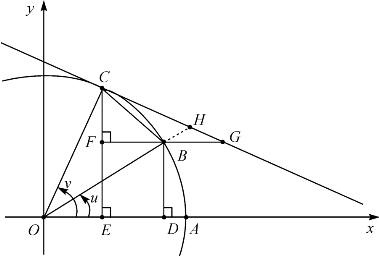
图6－4　cosx是sinx的乙函数的又一几何说明

习题6—7 应用（6－29）求cos44°的近似值.