在第2讲里引进了乙函数后，用两个例题来说明其应用.例题2－1表明，乙函数的正负可以用来判别其甲函数的增减；例题2－2表明，用乙函数可以计算甲函数的近似值.在第4讲，乙函数的作用进一步显现出来了.这些应用的根据，就是联系着函数F（x）和它的乙函数f（x）的估值不等式：在[u，v]上有p和q使有

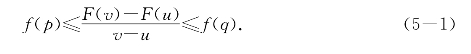
看来这个不等式是一大法宝.它的好处是用简单的一元函数来估计比较复杂的二元表达式.为了充分挖掘这个法宝的潜力，就要探索如何更有效地实现这个不等式的估值作用.

估值，就是从大小两头来限制中间的东西.如果两头互不关照，各奔天涯海角，中间的东西就落个逍遥自在，估不出所以然来.要想有效估值，两头的f（p）和f（q）就不能离得太远，即|f（p）－f（q）|不能太大，这就要对乙函数f（x）的性质有所要求.

应当首先关注哪一类函数呢？

函数千千万万，研究起来应有所选择.要由浅入深，由近及远，以期化难为易，执简御繁.数学课程就是这样安排的.

先是学了一次函数、反比函数、二次函数；进而认识指数函数、对数函数和幂函数；然后是三角函数和反三角函数.

由这些函数经过有限次的加减乘除和复合构成的函数，叫做初等函数.

函数可以用来描述变化.若变化起来比较平稳，|f（p）－f（q）|的大小易于控制，就容易研究；相反，变化剧烈的现象就难于掌握.平均变化率，即差商，是刻画函数变化速度的基本度量.判断函数变化是平稳还是剧烈，可以看差商.于是数学家就提出了下面的“差商有界”的概念.

定义4 （差商有界函数）设函数f（x）的定义域S由有限个区间组成.如果对于S的任意闭子区间[a，b]都有正数M，使得[a，b]中任意两数u和v都满足不等式

则称f（x）在S上差商有界.

若f（x）在闭区间[a，b]上差商有界，称f（x）在[a，b]上满足李普西兹（R.Lipschitz，1832—1903）条件.不等式（5－2）中的正数M叫做f（x）在[a，b]上的一个李普西兹常数.显然，李普西兹常数不是唯一的.

不等式（5－2）可写成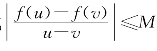，差商有界之名由此而来.

有界或无界是数学里的重要概念，它和数集合的上界或下界的概念密切相关.设S是实数集，M是一个实数.如果对任意的x∈S都有x≤M，则称M是S的一个上界；如果对任意的x∈S都有x≥M，则称M是S的一个下界.既有上界又有下界的数集合称为有界的数集合，值域为有界数集合的函数称为有界函数.

理解一个新的数学概念，最好的办法是举出具体的例子.要正面例子，也要反面的例子.

例题5—1 一次函数f（x）＝k·x＋b在（－∞，＋∞）上差商有界，它在任意闭区间[a，b]上有李普西兹常数M＝|k|.

证明 因为f（x）＝k·x＋b的差商为常数k，结论显然.

例题5—2 求证函数f（x）＝x2在（－∞，＋∞）上差商有界，并求它在区间[a，b]上的一个李普西兹常数.

解 对[a，b]上的任意两点u＜v，总有

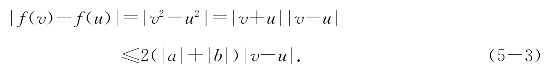
这表明函数f（x）＝x2在（－∞，＋∞）上差商有界，且M＝2（|a|＋|b|）是它在区间[a，b]上的一个李普西兹常数.

例题5—3 求证函数f（x）＝在（－∞，0）∪（0，＋∞）上差商有界，并求它在区间[a，b]（a·b＞0）上的李普西兹常数.

解 对[a，b]上的任意两点u＜v，总有

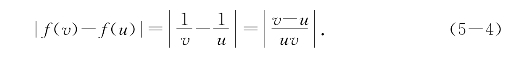
用m＝min{|a|，|b|}表示|a|和|b|中较小者，则|f（v）－f（u）|≤|v－u|，这表明函数f（x）＝在（－∞，＋∞）上差商有界，且M＝　是它在区间[a，b]上的一个李普西兹常数.

例题5—4 求证函数f（x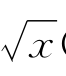）＝（x∈[0，＋∞））在[0，＋∞）上非差商有界但在（0，＋∞）上差商有界，并对0＜a＜b求它在[a，b]上的李普西兹常数.

解 为了指出f（x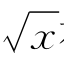）＝在[0，＋∞）上非差商有界，按定义只要证明它在[0，＋∞）的某个闭子区间上非差商有界，即不满足李普西兹条件即可.下面证明y＝在区间[0，1]上不是差商有界的.事实上，对于任意给定的正数M，当u＝0和v≤＜1时，总有

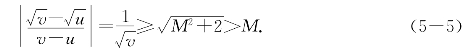
可见对于函数y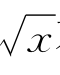＝不存在[0，a]上的李普西兹常数，即它不是差商有界的（图5－1）.

另一方面，当0＜a＜b时对[a，b]上任意两点u＜v，有

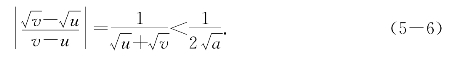
这表明y＝在区间（0，＋∞）上差商有界，且是它在[a，b]上的一个李普西兹常数.

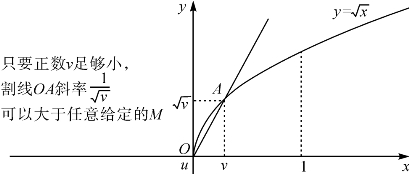
图5－1　函数y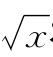＝在区间[0，1]上不是差商有界的

从几何上看，差商有界的函数，其曲线上任意两点所确定的割线斜率的绝对值有界.也就是不能太陡，而曲线y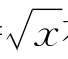＝在x＝0的切线平行于y轴，此点附近的割线要多么陡有多么陡，因而不可能满足李普西兹条件.

例题5—5 求证函数sinx和cosx都在（－∞，＋∞）上差商有界，且对任意两点u＜v有不等式

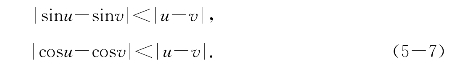
从而它们在任意区间[a，b]上有李普西兹常数M＝1.

解 根据三角函数的和差化积公式得

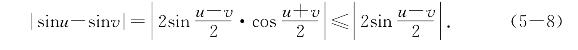
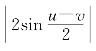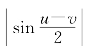当|u－v|≥π时显然有≤2＜π≤|u－v|；而|u－v|＜π时由熟知的几何事实可得当0＜x＜时有0＜sinx＜x（图5－2），从而有不等式＜；结合（5－8）得

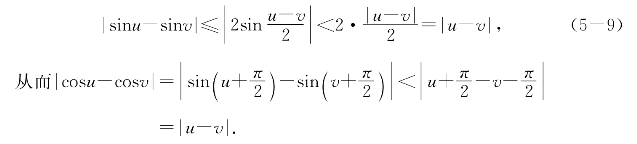
即所欲证.

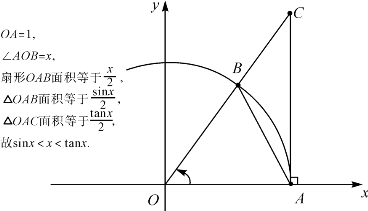
图5－2　一个关于正弦的不等式

例题5—6 求证函数f（x）＝x＋sinx在（－∞，＋∞）上递增，且其曲线上过任意两点的割线斜率小于2（图5－3）.

证明 对于u＜v，不等式（5－7）可以写成－1＜＜1的形式，从而有

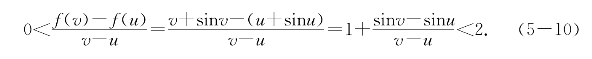
由差商的几何意义即得所要结论.

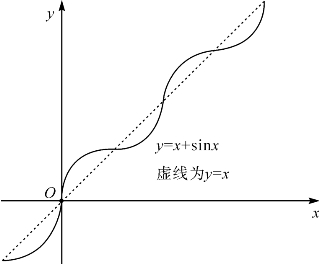
图5－3　函数f(x)＝x＋sinx的图像

差商有界函数的例子看了几个，该探讨其性质了.

命题5.1 （闭区间上差商有界函数必有界）设函数f（x）在区间[a，b]上差商有界，则有正数A使得对任意x∈[a，b]有|f（x）|＜A；即函数f（x）在区间[a，b]上有界.

证明 由条件可知f（x）在区间[a，b]上有李普西兹常数M，故

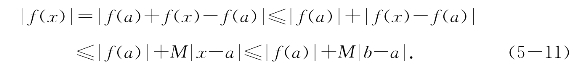
取A＝|f（a）|＋M|b－a|＋1，结论获证.(www.daowen.com)

由此可知，若f（x）有差商有界的乙函数，f（x）本身也差商有界.

命题5.2 若f（x）和g（x）都在闭区间[a，b]上差商有界，α和β是任意两个常数，则

（i）函数h（x）＝αf（x）＋βg（x）在[a，b]上差商有界；

（ii）函数H（x）＝f（x）·g（x）在[a，b]上差商有界；

（iii）若有正数m使对一切x∈[a，b]有|f（x）|＞m，则函数G（x）＝在[a，b]上差商有界.

证明 分别记f（x）和g（x）在[a，b]上的李普西兹常数为M和N，则对任意[a，b]上的u和v有

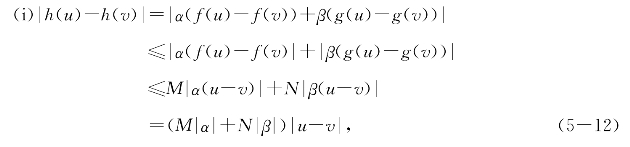
这证明了h（x）在[a，b]上差商有界；

（ii）由命题5.1知有正数A和B使当x∈[a，b]时有|f（x）|＜A和|g（x）|＜B，于是得

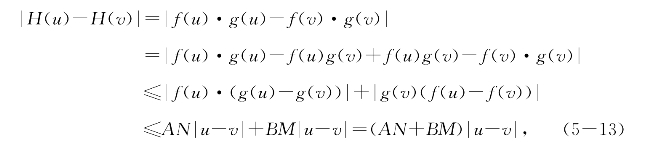
这证明了H（x）在[a，b]上差商有界；

（iii）在所设条件下有

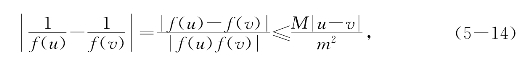
故在[a，b]上差商有界；再应用（ii），可知函数G（x）＝＝g（x）·在[a，b]上差商有界.

命题证毕.

命题5.3 若f（x）在闭区间[a，b]上差商有界，g（x）在闭区间[α，β]上差商有界且其值域包含于[a，b]，则函数ψ（x）＝f（g（x））在[α，β]上差商有界.

证明 设f（x）在[a，b]上的李普西兹常数为M，g（x）在[α，β]上的李普西兹常数为N，则对任意[α，β]上的u和v有

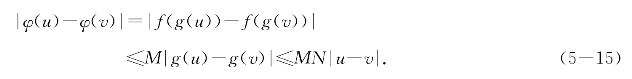
这表明ψ（x）＝f（g（x））在[α，β]上差商有界.

在上面几个命题中，不但证明了有关函数差商有界，还在（5－12）到（5－15）诸式中算出了其李普西兹常数，这些算式以后会有用处.

为了讨论反函数的差商，这里再明确一下反函数的概念.若g（x）的定义域S是f（x）的值域并取值于f（x）的定义域M，且对任意x∈S总有f（g（x））＝x，则称g（x）是f（x）的一个反函数.如果g（x）的值域就是f（x）的定义域M，易知对一切x∈M也有g（f（x））＝x，这时g（x）是f（x）的唯一的反函数，f（x）也是g（x）的唯一的反函数，称两者互为反函数.

例如，反正弦函数arcsinx的定义域是[－1，1]，这是sinx的值域；而arcsinx的值域包含于sinx的定义域（－∞，＋∞），且对一切x∈[－1，1]有sin（arcsinx）＝x，故arcsinx是sinx的一个反函数；同理，g（x）＝2π＋arcsinx也是sinx的一个反函数.若在上定义一个函数f（x）＝sinx，则f（x）和arcsinx互为反函数.

命题5.4 若f（x）在区间I上有定义且其值域为[A，B]，定义于[A，B]的g（x）是f（x）的一个反函数.若有正数m使对I中任意两数a和b有

则g（x）在[A，B]上差商有界.

证明 对于[A，B]中任意两数u和v，令a＝g（u）、b＝g（v）；因为g（x）是f（x）的一个反函数，故a＝g（u）、b＝g（v）都在I中，且f（a）＝u与f（b）＝v不同.这时不等式（5－16）成为

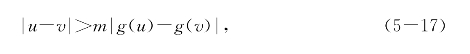
即|g（u）－g（v）|＜，可见g（x）在[A，B]上差商有界.

关于反函数的乙函数，则有下列事实：

命题5.5 设F（x）在[a，b]上单调递增，其值域为[A，B]；G（x）定义于[A，B]而值域为[a，b]，和F（x）互为反函数.如果f（x）在[a，b]上是F（x）的乙函数且恒为正，则是G（x）在[A，B]上的乙函数.

证明 任取[A，B]的子区间[u，v]，记G（u）＝y和G（v）＝z.因f（x）是F（x）的乙函数，故有[y，z]上的r和s使得

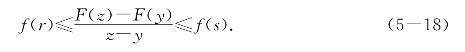
记F（s）＝p和F（r）＝q，将y＝G（u）、z＝G（v）、s＝G（p）和r＝G（q）代入得

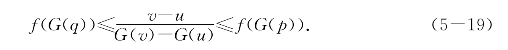
此不等式取倒数得

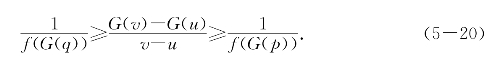
即推知　是G（x）的乙函数.证毕.

从上面几个命题看，差商有界函数是很广泛的一类函数.例如，所有的多项式函数都是差商有界的；可以写成有理分式的函数除了个别点也是差商有界的.下面会看到，初等函数除了个别点外都是差商有界的.

我们这样关心差商有界的函数，它有什么好的性质呢？

命题5.6 （差商有界函数的连续性）设f（x）在开区间I上差商有界而A＜B是任意两数，p是I中一点使f（p）∈（A，B）.则必有两数α＜β满足p∈（α，β）⊆I，使对任意x∈（α，β）有f（x）∈（A，B）.

在证明此命题前，最好先直观地看看这个命题包含了什么意义.为了简便，这里和今后都把包含点p的开区间叫做p的一个邻域.如此一来，命题中的（A，B）不过就是f（p）的一个邻域，而（α，β）是p的某个邻域.于是命题告诉我们，差商有界函数f如果把p变到f（p），就必然把p的某个领域的所有点变到f（p）的邻域中！这大有“一人得道，鸡犬飞升”之意！

具体一些，如果（A，B）＝（0，＋∞），f（p）∈（A，B）即f（p）＞0；如果（A，B）＝（－∞，0），f（p）∈（A，B）即f（p）＜0；因此作为命题的特款就可以断言：若f（p）＞0则f在p的某个邻域全取正值，若f（p）＜0则f在p的某个邻域全取负值！这叫“保号性”.

具有命题5.6结论所述性质的函数叫做I上的连续函数.命题5.6也就是说：差商有界函数是连续函数.注意连续函数不一定差商有界.容易验证f（x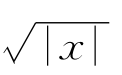）＝在（－∞，＋∞）上具有命题5.5结论所述性质，但从例题5－4可知它不是差商有界的.

命题5.6的证明 在I中取两数a、b使a＜p＜b因为f（x）在开区间I上差商有界，故有正数M使对[a，b]中的点x有

记d＝min{|f（p）－A|，|f（p）－B|}，δ＝Md，则当x∈（p－δ，p＋δ）时总有|x－p|＜δ＝，从而|f（x）－f（p）|≤M|x－p|＜Mδ＝d，即f（x）∈（A，B）.令α＝p－δ且β＝p＋δ，即为所求（图5－4）.

命题5.6刻画了连续函数的本质.后面将进一步阐述其重要应用.讨论一般的连续函数难度偏大，所以我们知难而退，将比较容易把握的差商有界函数作为主要研究对象.对差商有界函数熟悉清楚之后，再推广到一般情形是很容易的.

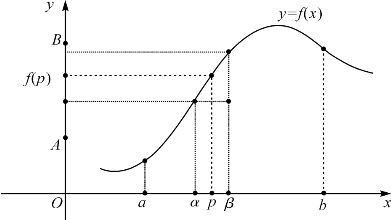
图5－4　差商有界函数f把p的邻域映到f(p)的邻域

习题5—1 求证函数f（x）＝|x|在（－∞，＋∞）上差商有界，并求它在[a，b]上的一个李普西兹常数.

习题5—2 求证函数f（x）＝x3在（－∞，＋∞）上差商有界，并求它在区间[a，b]上的一个李普西兹常数.

习题5—3 求证函数f（x）＝x＋在（－∞，0）∪（0，＋∞）上差商有界，并求它在区间[a，b]（a·b＞0）上的一个李普西兹常数.

习题5—4 求证函数f（x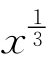）＝（x∈（－∞，＋∞））在（－∞，＋∞）上非差商有界，但在不含0的任意区间上差商有界；并对0＜a＜b求它在[a，b]上的一个李普西兹常数.

习题5—5 求证函数f（x在（－∞，＋∞）上差商有界，并求它在[a，b]上的一个李普西兹常数.

习题5—6 设函数f（x）在[a，b]上有李普西兹常数M，求证函数g（x）＝f（x）－（M＋0.001）x在[a，b]上递减.

习题5—7 在[a，b]上任取两点u和v可以确定函数f（x）＝x2在u和v处的差商Q（u，v）.请讨论Q（u，v）的取值范围.