就在笛卡儿发表求切线的“圆法”那年，同为解析几何创始人之一的费马（P.Fermat，1601—1665）在一封信中提出了求极大值和极小值的代数方法.费马的方法也可以用来求切线，是微积分早期引起热烈讨论的一项重要工作.

数学中的最大值或最小值，和日常语言中的意义相同；而极大值或极小值，就和日常理解的意义有些出入了.

若函数f（x）在包含x＝x0的一个数集S上有定义，且对任一点x∈S总有f（x）≤f（x0）（f（x）≥f（x0）），则称f（x）在S上取到最大（小）值f（x0），并称x＝x0是f（x）在S上的最大（小）值点，最大值和最小值通称最值.当数集S容易从上下文确定时可以略去不提.

若f（x）在包含x0的一个开区间Δ上有定义，且在Δ上取到最大（小）值f（x0），则称x＝x0是f（x）的一个极大（小）值点，并称f（x0）是f（x）的一个极大（小）值.极大值和极小值通称极值.

简言之，极值与左邻右舍比起来是最值，是小组冠军.

费马设想，如果函数f（x）在x＝u取到极大，则有一个含u的小区间Δ＝（ud，u＋d），使得对于任意的u＋h∈Δ，有f（u＋h）≤f（u）.

于是当h≠0时，不论h＞0或h＜0都有

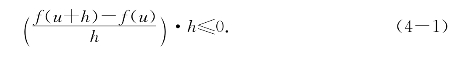
设当h趋于0时趋于一个确定的数A.若A是正数，当h＞0时将有A·h＞0，若A是负数，当h＜0时将有A·h＞0，都和（4－1）矛盾，故必有A＝0.

同理，在极小的情形也必有A＝0.

前面已经知道，若当h趋于0时趋于一个确定的数A，则A是f（x）在x＝u处的导数，即f′（u）＝A；从几何上看导数是函数曲线的切线的斜率.因此，费马的想法实质就是说，f（x）在x＝u处取到极值的必要条件，是f′（u）＝0；亦即函数曲线在这一点的切线应当是水平的，如图4－1.

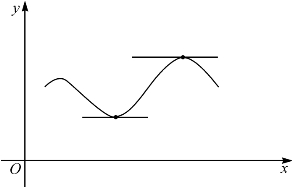
图4－1　函数曲线在极值点处的切线

费马用一个简单的例子说明他的方法.这是一个小学生熟悉的问题：设矩形的两边之和为b，何时其面积最大？

用x表示矩形的一边，则另一边为b－x.于是矩形面积可以表示为x的函数f（x）＝x（b－x）＝bx－x2.设它在x＝u处取到极大，则差商

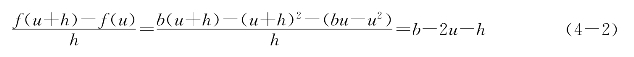
当h趋于0时应趋于0，可见b－2u＝0，求出u＝.也就是说只有当此矩形为正方形时其面积才取到极值.稍加讨论便知矩形为正方形时其面积最大.

由于问题的求解涉及h趋向于0的过程，要说清楚颇费工夫.如果基于乙函数的概念来讨论，问题就简单了.事实上，如命题2.9所述，若g（x）是f（x）的乙函数，则由g（x）为正（负）可以得知f（x）递增（减）；由g（x）非正（负）可以得知f（x）不增（减）.但常常有g（x）在开区间（u，v）为正（负）但在一个或两个端点处等于0的情形，如例题2－1中g（x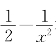）＝在区间，＋∞）为正但在端点x＝处为0，这样能否断定f（x）在，＋∞）递增？当时没有理清这个细节，只是画出图来看看就忽悠过去了.下面把这种情形说清楚，从而建立一个更方便地判断函数增减性的工具.

命题4.1 设g（x）是f（x）在区间I上的乙函数，u＜v是I中的两点，若g（x）在（u，v）上为正且在[u，v]上非负，则f（x）在[u，v]上递增；若g（x）在（u，v）上为负且在[u，v]上非正，则f（x）在[u，v]上递减.

证明 应用命题2.9或直接根据乙函数定义，若g（x）在（u，v）上为正且在[u，v]上非负，则f（x）在（u，v）上递增且在[u，v]上不减.

为进一步证明f（x）在[u，v]递增，用反证法，设f（x）在[u，v]上仅仅是不减而非递增，则有[u，v]上两点s＜t使f（s）＝f（t），因而f（x）在[s，t]上为常数，于是f（x）在（u，v）的子区间（s，t）上为常数.这与f（x）在（u，v）上递增的结论矛盾，从而否定了反证法假定.这证明了f（x）在[u，v]上递增.

同理可证若g（x）在（u，v）上为负且在[u，v]上非正，则f（x）在[u，v]上递减.详细推导留给读者.

有趣的是，命题4.1中的条件g（x）在[u，v]上非负和g（x）在[u，v]上非正都是可以去掉的.这在前面已经作为第2讲的习题叙述过了.证明起来如有困难也可参看书后的习题解答.

从上面的命题立刻得到函数取到极大或极小的常用判别法.

命题4.2 （极值判别法）设g（x）是f（x）在区间I上的乙函数，u＜v是I中的两点而x0∈（u，v）使g（x0）＝0；若g（x）在（u，x0）上为正、在（x0，v）上为负，则f（x）在x＝x0处取到极大；若g（x）在（u，x0）上为负、在（x0，v）上为正，则f（x）在x＝x0处取到极小.

于是，要求函数f（x）＝x（b－x）＝bx－x2的极大极小值，只要写出它的乙函数g（x）＝b－2x，并根据乙函数的正负来判断其增减性.显然有，且g（x）在上为正、在上为负，故f（x）在x＝处取到极大值，显然这也是f（x）在（－∞，＋∞）上的最大值.所有这些都不用趋于0之类的描述，道理简单明白.

照此办理，二次函数的增减性和最大最小值的问题容易解决.

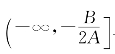命题4.3 设f（x）＝Ax2＋Bx＋C（A≠0，x∈（－∞，＋∞）），则当A＞0时f（x）在x0＝－处取到最小值，且f（x）在上递减，在递增；当A＜0时f（x）在x0＝－处取到最大值，且f（x）在上递　增，在递减.

证明 由命题2.3和2.5可知g（x）＝2Ax＋B是f（x）＝Ax2＋Bx＋C的乙函数.当A＞0时，由，且g（x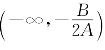）在上为负，在上为正，故由极值判别法（命题4.2）知道f（x）在x0＝－处取到最小值，且f（x）在上　递　减，在上递增；当a＜0时有同理，具体推导留给读者.

注意到二次方程Ax2＋Bx＋C＝0的判别式为Δ＝B2－4AC，则此二次函数的最值可以简单地写成便于记忆的.

上述命题说明二次函数在（－∞，＋∞）上只有一个极值，也就是最值.如果考虑它在闭区间上的最值，就还要看其极值点是否在此区间内，并且要考虑两端点处的函数值.

例题4—1 （i）求函数f（x）＝x2－2x－t在区间[0，3]上的最大值；

（ii）求函数F（x）＝|x2－2x－t|在区间[0，3]上的最大值.

解 （i）应用命题4.3，可知f（x）＝x2－2x－t在x0＝1∈（0，3）处取到极小值－1－t，于是f（0）＝－t和f（3）＝3－t中较大者3－t即为所求的最大值.

（ii）当f（x）＝x2－2x－t的最小值－1－t≥0时即t≤－1时，函数F（x）＝|x2－2x－t|＝f（x），其最大值为F（3）＝f（3）＝3－t，如（i）.

当f（x）＝x2－2x－t的最小值－1－t＜0时即t＞－1时，F（x）＝|x2－2x－t|在x0＝1∈（0，3）处取到极大值1＋t＞0，如图4－2.于是F（1）＝1＋t、F（0）＝|t|和F（3）＝|3－t|中较大者为所求的最大值.有三种情形：（1）当t∈（－1，1）时F（3）＝|3－t|＞2显然为最大；（2）t＝1时F（1）＝2＝F（3）同为最大值；（3）t＞1时F（1）＝1＋t为最大.这三种情形如图4－3.

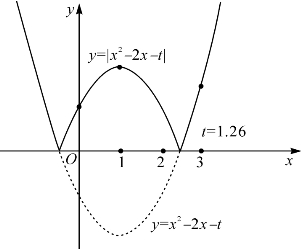
图4－2　函数F(x)＝|x2－2x－t|的图像

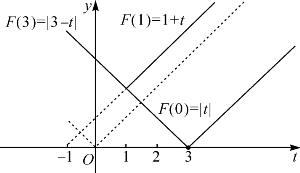
图4－3　三个函数值随参数t变化时的比较

比二次函数复杂一点的是三次函数，为了研究三次函数的增减性和极值，自然想到要找它的乙函数.

例题4—2 求证：函数g（x）＝3x2是f（x）＝x3的乙函数.

解 计算得

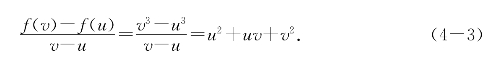
当uv≥0时，u2＋uv＋v2显然在g（u）＝3u2和g（v）＝3v2之间；这表明在（－∞，0]和[0，＋∞）上，g（x）＝3x2都是f（x）的乙函数.

能不能由此推出在（－∞，＋∞）上函数g（x）＝3x2是f（x）的乙函数呢？

确实有这样的一般规律.

命题4.4 （乙函数的区间可分性）若g（x）是式f（x）在区间I上的乙函数，又是f（x）在区间J上的乙函数，且区间I和区间J有公共点，则g（x）是f（x）在区间K＝I∪J上的乙函数.

证明 按定义，只要证明对K＝I∪J的任意子区间[u，v]，总有[u，v]中的点p和q，使有下列不等式

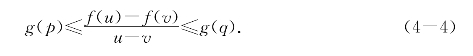
若[u，v]是I或J的子区间，结论显然.若不然，则有I和J的公共点a∈（u，v）使得[u，a]和[a，v]分别包含于I和J.

注意到差商总在和之间（图4－4）.因g（x）是f（x）在[u，a]和[a，v]上的乙函数，故在[u，a]上有p1、q1使得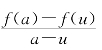在g（p1）和g（q1）之间；同理在[a，v]上有p2、q2使得在g（p2）和g（q2）之间；令g（p）和g（q）分别为此4值中的最小和最大者，则有（4－4）成立.证毕.

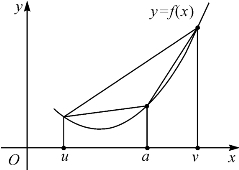
图4－4　差商总在和之间

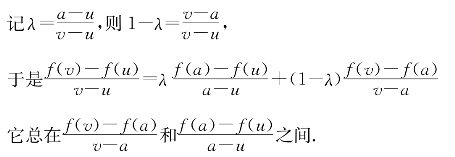
上述命题显然可以推广到任意多个区间之并的情形，所以在求乙函数时就可以对区间分段处理了.

有了乙函数的区间可分性，就可以确认3x2在（－∞，＋∞）上是x3的乙函数.这使我们猜想到，3x2＋2ax＋b是x3＋ax2＋bx＋c的乙函数.

命题4.5 g（x）＝3x2＋2ax＋b在（－∞，＋∞）上是f（x）＝x3＋ax2＋bx＋c的乙函数.

证明 求出f（x）在[u，v]上的差商，记作

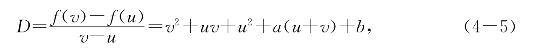
考虑它和g（u）以及g（v）之差：

因为（v－u）＞0，故当v＞u≥－时，上面两式都为正，即g（u）＜D＜g（v），说明在上g（x）是f（x）的乙函数；当u＜v≤－时，两者都为负，即g（v）＜D＜g（u），说明在上g（x）也是f（x）的乙函数.故在（－∞，＋∞）上g（x）是f（x）的乙函数.证毕.

应用命题2.3于上述结果，可知3ax2＋2bx＋c是更一般的三次函数ax3＋bx2＋cx＋d的乙函数.

作为习题，请读者验证3ax2＋2bx＋c是三次函数ax3＋bx2＋cx＋d的导数.这种看似巧合的情形将在第6讲得到解释.

于是三次函数的增减性和极大极小问题完全归结为二次函数的正负，从而就完全解决了.(www.daowen.com)

命题4.6 设f（x）＝ax3＋bx2＋cx＋d（a≠0，x∈（－∞，＋∞）），则有

（i）若b2－3ac≤0，当a＞0时f（x）在（－∞，＋∞）上递增，a＜0时f（x）在（－∞，＋∞）上递减；

（ii）若b2－3ac＞0，设u＜v是方程3ax2＋2bx＋c＝0的两个实根，则f（x）的增减性和极大极小情形如下：

若a＞0，则f（x）在（－∞，u]和[v，＋∞）上递增，在[u，v]上递减；在x＝u处取极大，在x＝v处取极小；

若a＜0，则f（x）在（－∞，v]和[v，＋∞）上递减，在[u，v]上递增；在x＝u处取极小，在x＝v处取极大.

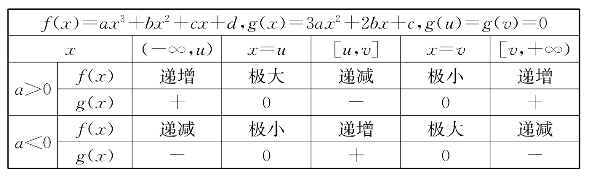
列出下表，一目了然.

表4－1　三次函数的增减性和极值(b2－3ac＞0情形)

证明 由命题4.5，g（x）＝3ax2＋2bx＋c在（－∞，＋∞）上是f（x）＝ax3＋bx2＋cx＋d的乙函数.考虑二次函数

g（x）＝Ax2＋Bx＋C（A＝3a，B＝2b，C＝c），

结合命题4.3可得：

（i）若B2－4AC＝b2－3ac≤0，当A＝3a＞0时g（x）在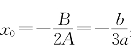处取到最小值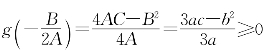，故g（x）在（－∞，＋∞）上除x0＝－一点外均为正，由命题4.2可知f（x）在（－∞，＋∞）上递增；a＜0时g（x）在x0＝－处取到最大值，故g（x）在（－∞，＋∞）上除x0＝一点外均为负，由命题4.2可知f（x）在（－∞，＋∞）上递减（如图4－5和4－6）.

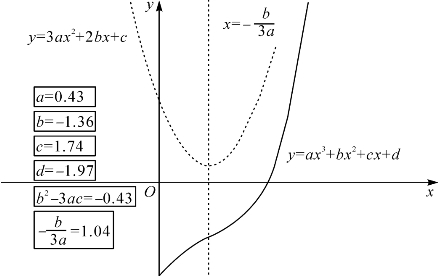
图4－5　三次函数ax3＋bx2＋cx＋d曲线1(b2－3ac≤0且a＞0)

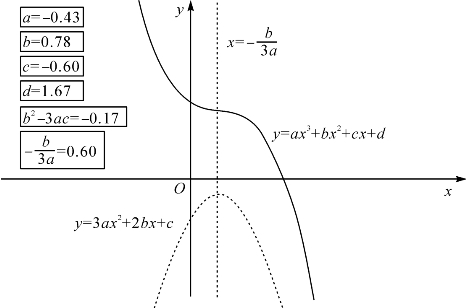
图4－6　三次函数ax3＋bx2＋cx＋d曲线2(b2－3ac≤0且a＜0)

（ii）若B2－4AC＝b2－3ac＞0，当A＝3a＞0时g（x）在x0＝－∈（u，v）处取到最小值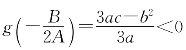，故g（x）在（－∞，u）和（v，＋∞）上为正而在（u，v）上为负，由命题4.2可知f（x）在（－∞，u]和[v，＋∞）上递增而在[u，v]上递减，在x＝u取到极大，在x＝v取到极小；a＜0时g（x）在x0＝－∈（u，v）处取到最大值＞0，故g（x）在（－∞，u）和（v，＋∞）上为负而在（u，v）上为正，由命题4.2可知f（x）在（－∞，u]和[v，＋∞）上递减而在[u，v]上递增，在x＝u取到极小，在x＝v取到极大（如图4－7和图4－8）.

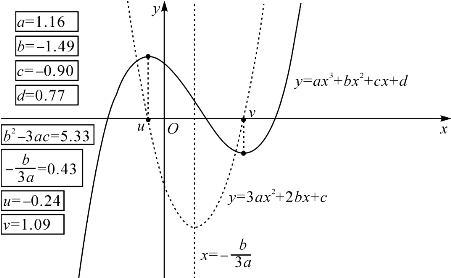
图4－7　三次函数ax3＋bx2＋cx＋d曲线3(b2－3ac＞0且a＞0)

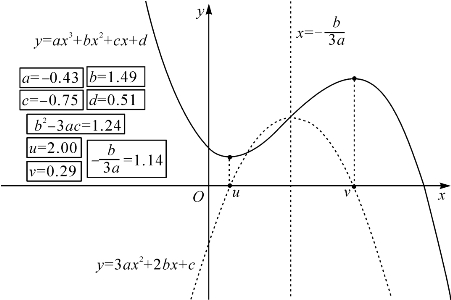
图4－8　三次函数ax3＋bx2＋cx＋d曲线4(b2－3ac＞0且a＜0)

例题4—3 设函数f（x）＝x3＋ax2＋x＋1（a∈（－∞，＋∞），x∈（－∞，＋∞））.

（i）讨论函数f（x）的单调区间；

（ii）设函数f（x）在区间（1，5）内是减函数，求a的取值范围.

解 函数g（x）＝3x2＋2ax＋1是f（x）＝x3＋ax2＋x＋1的乙函数，f（x）的增减性可从g（x）＝3x2＋2ax＋1的正负得出.

（i）当（2a）2－4×3≤0即a2≤3时g（x）≥0，f（x）在（－∞，＋∞）上递增；

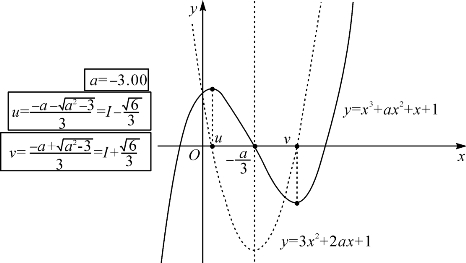
图4－9　函数f(x)＝x3＋ax2＋x＋1的单调区间

当a2＞3时g（x）＝0有两根u＝和v＝，可知f（x）在（－∞，u]和[v，＋∞）上递增，在[u，v]上递减（如图4－9）.

（ii）解不等式u≤1＜5≤v，即－a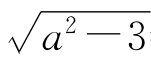－≤3且15≤－a＋，

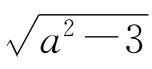解得a≤－7.6.

例题4—4 如图4－10是一张长为30cm、宽为20cm的矩形纸片.从虚线处将四边折叠并适当粘贴起来构成一个高为xcm、长为（30－2x）cm、宽为（20－2x）cm的无盖纸盒（图4－11）.问纸盒的高是多少时容积最大？容积最大是多少？

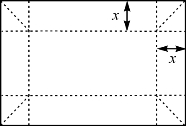
图4－10　矩形纸片

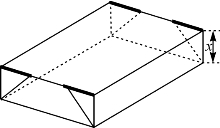
图4－11　矩形纸片折叠成纸盒

解 纸盒容积可表示成其高度x的函数

而g（x）＝4（3x2－50x＋150）是V（x）的乙函数，如图4－12.求出g（x）＝0的两根为u＝≈3.92和v＝≈12.74.于是V（x）在[0，u]递增，在[u，10]递减，在[0，10]上有最大值V（u）≈V（3.92）.即纸盒的高约为3.92cm时容积最大，容积最大约为V（3.92）≈1056.3（cm3）.

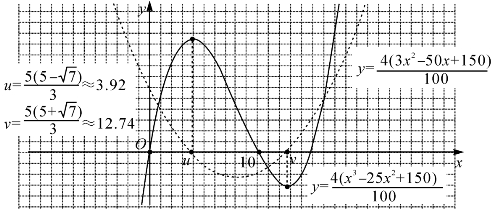
图4－12　纸盒的最大容积(y轴l格表100cm3)

例题4—5 已知函数f（x）＝k（x＋1）＋（x≠0）在（0，3]上递减，求参数k的取值范围.

解 由命题2.3和2.6知g（x）＝k－是f（x）的乙函数.想要f（x）在（0，3]上递减，应有k－在（0，3]上非正，解得k≤，图4－13是k＝的临界情形.（曲线平缓，仅靠直观很难准确看出结论！）

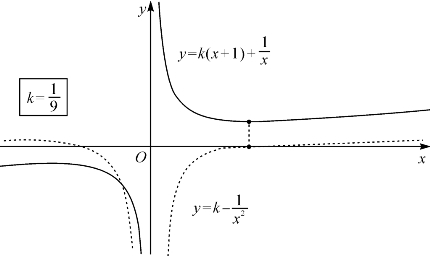
图4－13　函数f(x)＝k(x＋1)＋的递减区间

例题4—6 设F（x）＝在[0，＋∞）上有定义，请确定参数a的变化范围和F（x）的单调区间.

解 记f（x）＝x＋a＋1，由命题2.3和2.7可知g（x）＝1＋是f（x）在（0，＋∞）上的乙函数，于是

（i）若a≥0，此时在（0，＋∞）上有g（x）＞0，从而f（x）在（0，＋∞）递增.因f（0）＝1显然为最小值，故f（x）实际上在[0，＋∞）递增.于是F（x）＝在[0，＋∞）上递减且F（0）＝1为最大值.如图4－14.

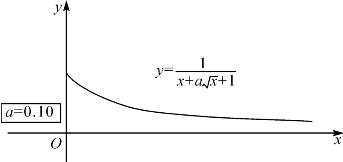
图4－14　函数F(x)＝当a≥0时递减

（ii）若a＜0，记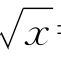＝t从而

f（x）＝f（t2）＝t2＋at＋1，

二次方程f（t2）＝0的判别式为a2－4，故当a∈（－2，0）时f（x）在[0，＋∞）上恒正.

又因f（t2）在t＝－处取到最小、在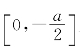上递减、在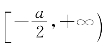上递增，故f（x）在x＝处取到最大、在上递增、在上递减，如图4－15.而当a≤－2时方程f（x）＝f（t2）＝t2＋at＋1＝0有正根t1＝，与F（x）＝在[0，＋∞）上有定义不合.

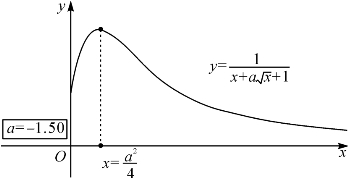
图4－15　函数F(x)＝当－2＜a＜0时的单调区间

综上可知，参数a的范围为（－2，＋∞）；当a∈[0，＋∞）时F（x）在[0，＋∞）上递减，当a∈（－2，0）时F（x）在上递增，在上递减.

习题4—1 用第1讲的方法求f（x）＝ax3＋bx2＋cx＋d的导数.

习题4—2 求函数f（x）＝x3－12x＋8在区间[－3，3]上的最大值与最小值.

习题4—3 求函数f（x）＝t·x2＋2t2·x＋t－1（x∈（－∞，＋∞），t＞0）的最小值h（t），并求h（t）＋t在区间（0，2）上的取值范围.

习题4—4 若函数F（x）＝x－在（－5，－1）上递增，求F（x）在[1，3]上的最大值.

习题4—5 已知函数f（x）＝在区间[－1，1），（1，3]上各有一个极值点，求a2－4b的最大值.

习题4—6 已知函数f（x）＝2x3＋3ax2＋3bx＋8c在x＝1及x＝2时取得极值，求f（x）在[0，3]上的最大值和最小值.

习题4—7 设函数f（x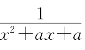）＝的表达式在（－∞，＋∞）上有意义，求a的取值范围和f（x）的递减区间.

习题4—8 设正圆锥的高为30，底半径为10，求其内接圆柱体的体积的最大值.