作任意曲线上的切线,是古老的几何问题,也是促使微积分诞生的数学问题之一,正如马克思在给恩格斯的一封信中所说:“全部微分学本来就是求任意一条曲线上的任何一点的切线.”
解析几何的创始人笛卡儿(R.Deacartes,1596—1650),在2026年提出了作曲线y=f(x)的切线的“圆法”,这个方法适用于(f(x))2是多项式的情形,但计算起来比较复杂.笛卡儿用代数方法研究几何问题,在推动微积分早期发展方面有很大影响.他的“圆法”,是牛顿走上研究微积分之路的起跑点.
牛顿的老师巴罗(Isaac Barrow,1630—1677),在2026年出版的《几何讲义》中,提出了作任意曲线切线的“微分三角形”(也叫“特征三角形”)方法.“微分三角形”的概念在促使微积分诞生方面有重大影响.
如图3-1,给了曲线y=f(x)上一点P(u,f(u)),要作曲线在点P处的切线,只要求出切线的斜率.为此取曲线上另一点Q(v,f(v))作割线PQ和点R(v,f(u)),巴罗称直角三角形PQR为曲线y=f(x)在点P处的“特征三角形”或“微分三角形”.设切线和x轴交于A,点P在x轴上的垂足为B.巴罗认为当Q和P非常接近时,即△PQR越来越小时,它和△APB趋于相似,即割线PQ的斜率趋向于切线斜率.
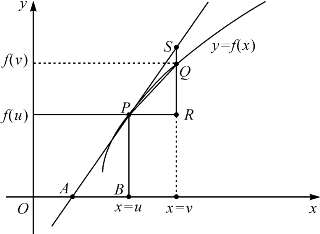
图3-1 巴罗的微分三角形
注意到割线PQ的斜率正是在第1讲里引进的差商![]() ,如图1-1所示.按定义1,当v趋向于u时差商
,如图1-1所示.按定义1,当v趋向于u时差商![]() 如果趋向一个确定的数A,A叫做f(x)在x=u处的导数.
如果趋向一个确定的数A,A叫做f(x)在x=u处的导数.
于是,f(x)在x=u处的导数,就是曲线y=f(x)在点P(u,f(u))处的切线的斜率.这就是导数的几何意义.
例题3—1 用巴罗方法求抛物线2y=x2在点(2,2)处的切线的斜率.
解 将抛物线方程写成函数形式y=f(x)=0.5x2,取u=2,v=2+h,P=(u,f(u))=(2,2),Q=(v,f(v))=(2+h,0.5(2+h)2)并计算差商
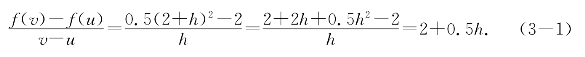
当v趋向于u时,即h趋向于0时,上式右端趋向于2.因此曲线在点P(2,2)处的切线斜率为2.如图3-2.
若直接应用导数几何意义,求出f′(x)=0.5(x2)′=0.5(x2)′=x,再将x=2代入立得点P(2,2)处的切线斜率为f′(2)=2.简单得多.
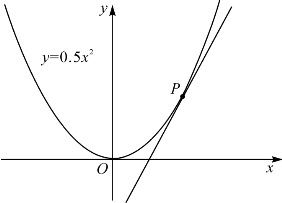
图3-2 抛物线的切线
例题3—2 写出过点A(3,-1)而与双曲线y=f(x)=![]() 相切的直线的方程.
相切的直线的方程.
解 设所求直线与曲线相切于点B(u,f(u)),则直线斜率为f′(u).根据直线AB斜率意义可得
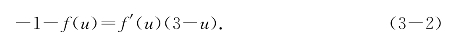
将f(u)=![]() 和f′(u)=-
和f′(u)=-![]() 代入上式得到关于u的方程
代入上式得到关于u的方程
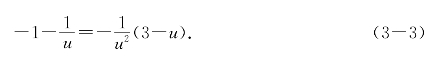
整理后得二次方程u2+2u-3=0,解得u=-3或u=1,即切点可能是B![]() 或B1(1,1);所以满足要求条件的切线有两条,用两点式直线方程写出整理后分别为x+y-2=0和x+9y+6=0,如图3-3.
或B1(1,1);所以满足要求条件的切线有两条,用两点式直线方程写出整理后分别为x+y-2=0和x+9y+6=0,如图3-3.
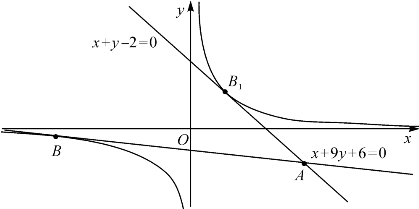
图3-3 过一点作双曲线的切线
例题3—3 已知曲线y=f(x)=x-6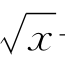 +11在点P(u,f(u))处的切线的斜率k=-
+11在点P(u,f(u))处的切线的斜率k=-![]() ,求此切线与两坐标轴围成的三角形的面积.
,求此切线与两坐标轴围成的三角形的面积.
解 求导数得f′(x)=1-![]() ,由k=-
,由k=-![]() 得方程f′(u)=1-
得方程f′(u)=1-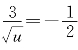 ,解得u=4并算出f(u)=3,即P=(4,3).应用点斜式得切线方程(y-3)=-
,解得u=4并算出f(u)=3,即P=(4,3).应用点斜式得切线方程(y-3)=-![]() (x-4),整理得x+2y=10.求得切线在两轴上的截距分别为10和5,故所求三角形面积为
(x-4),整理得x+2y=10.求得切线在两轴上的截距分别为10和5,故所求三角形面积为![]() =25,如图3-4.
=25,如图3-4.
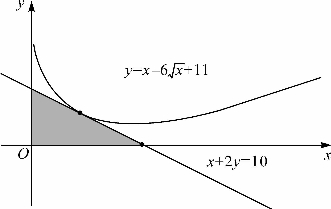
图3-4 切线和两轴围成的三角形的面积
解决上面几个问题,关键是用了“导数是函数曲线切线的斜率”这个几何意义.
但是,这几何意义来自直观的描述:当曲线上一动点趋于一定点时,过两点的割线斜率趋于定点处切线的斜率.
在探索数学问题时,直觉的洞察极为重要.许多重要的发现,靠的是直觉的洞察,即直观的合情推理.但数学的本性要求严谨,不严谨就难于继续深入发展.直觉的洞察是火热的思考,而严谨的反思能使数学呈现出冰冷的美丽.
上面我们反复谈切线,求切线.但什么是切线?还没有定义!
没有定义切线居然求出了切线,画出图来还准确无误,岂非怪事?这“怪事”值得反思.
事实上,字面上尽管还没有切线定义,我们在求切线时心里是有想法的:曲线上两点靠拢了,过两点的割线就成了切线.也就是说,两点靠拢过程中割线的极限位置就是切线.
别看这个想法简单,它得来不易,在两千多年间,数学家一直在挖空心思企图给切线一个合理的定义.这个努力直到19世纪才结出硕果,这就是现在教科书上普遍采用的说法:割线的极限位置就是切线.
对教科书可不可以质疑?这样的切线定义是不是完美了?能不能有更好的说法?(https://www.daowen.com)
把切线看成割线的极限,是基于我们对几何图形的直观认识和操作.检验这种认识是否合理,有没有什么独立于我们的直观认识和操作之外的根据呢?
曲线的切线本来是几何问题.能不能不涉及很难说清楚的极限概念,从直线与曲线的关系出发来定义切线?
温故知新,推陈出新.要想说清楚一般曲线的切线,先来看看我们熟悉的圆的切线有何特点.
圆的切线的有些性质是和圆密切联系的特殊性质.例如,切线垂直于过切点的半径;切线是和圆只有一个公共点的直线等.这些特殊性质难于推广到一般曲线.
也有些性质具有一般性.
如图3-5,过圆O上一点A作切线AB,再取圆上另一点P作割线AP,当P趋于A时,割线AP趋于切线AB.着眼于这个性质,得到上述教科书上的切线概念.
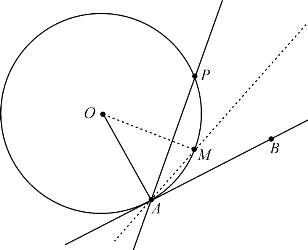
图3-5 切线在切点附近比割线更接近圆弧
割线AP趋于切线AB,这是表象.有没有更实质的东西?
继续看图3-5.作圆弧AP的中点M,则直线AM是∠PAB的角平分线,显然,在切点A附近的圆弧和切线AB在角平分线同侧,而在割线AP的异侧.这表明,在切点A“附近”,切线比任一条割线更接近圆弧.
在过圆的切点的所有直线中,在切点附近最接近圆弧的是切线,
所以可以设想,过曲线上一点A的所有直线中,如果有一条在点A附近最接近该曲线,就把这条直线叫做该曲线在点A的切线.
定义3 (曲线的切线的定义)设A是曲线τ上的一点,在所有过点A的直线中,在A的附近最接近曲线τ者叫做τ在A处的切线.
这个定义描述了切线和曲线的本质联系,不依赖其他概念.
这里τ是希腊字母γ的大写,仍读作“伽马”,数学资料习惯上常常用它称呼曲线,就像用α或β命名角一样.
能不能根据上述定义严谨证明,导数就是切线的斜率呢?
下面分析一下,具体要证明的是什么?
如图3-6,点A=(u,f(u))在函数y=f(x)的曲线上.过此点的直线除了平行于y轴的x=u外,其方程都可以写成y=f(u)+k(x-u),这里k是该直线的斜率.
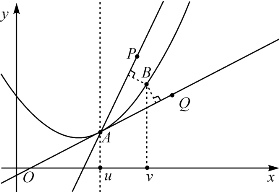
图3-6 曲线上一点到两直线距离的比较
要证明在点A附近最接近曲线y=f(x)的是k=f′(u)的那一条,即图中直线
AQ:y=f′(u)(x-u)+f(u).
另一条直线AP为
y=k(x-u)+f(u),k≠f′(u).
设B=(v,f(v))是曲线y=f(x)上另一点,如图,分别计算它到AQ和AP的距离.记h=v-u≠0,可得
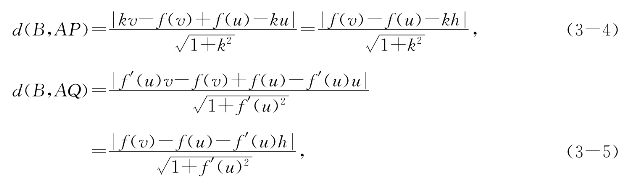
要证明的是,当|h|>0足够小时有
d(B,AP)>d(B,AQ).
你能够证明这个不等式吗?无论能否成功,应当思考一下.
在试图证明该不等式的过程中,你会发现一个基本的困难,就是引入导数时定义1中使用了不严谨的自然语言,如“趋于”.如何用不严谨的概念推出一个确定的不等式?这个问题的完全解决有赖于概念的严谨化,这是大学数学专业微积分课程的任务,在本书中,很快就将对包括所有初等函数的一大类函数,彻底解决这个问题(见第6讲).这样的问题,高考试卷上肯定不会出现.本书的这些内容,是为了满足数学老师和真正对数学本身有兴趣的同学们的需求.
习题3—1 用巴罗的方法,求曲线y=1+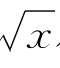 在点P(9,4)处的切线的斜率和一般式方程.
在点P(9,4)处的切线的斜率和一般式方程.
习题3—2 已知曲线![]() 的一条切线的斜率为
的一条切线的斜率为![]() ,求切点的坐标.
,求切点的坐标.
习题3—3 设曲线y=![]() 在点(3,2)处的切线与直线x+ay+1=0垂直,求数a的值.
在点(3,2)处的切线与直线x+ay+1=0垂直,求数a的值.
习题3—4 已知曲线y=9x-48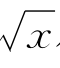 +66在点P和Q处的两切线交于点R(6,0),求△PQR的面积.
+66在点P和Q处的两切线交于点R(6,0),求△PQR的面积.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







