数学解题提倡一题多解.寻找平均速度与瞬时速度的关系，还有没有别的思路呢？现在请你合上书想想，平均速度与瞬时速度有何关系？

这可是一个挑战性的问题.几百年来，甚至可以说两千多年间，无数杰出的数学家中，只有牛顿给出了一种解答.而且是数学上说不清的解答.为了说清楚这个解答，数学家继续思考了150多年.

现在希望一题多解.

我们问，还有没有第二种解答？

如果你希望自己把答案想出来，就收起书，把问题放在心里，也许你几分钟就想出来了，也许要用你几年.爱因斯坦上中学的时候，曾经用三个星期的时间独立思考，自己证明了勾股定理.

当然，成功的路不止一条，不一定要学爱因斯坦.如果你等不得，就看下去.

瞬时速度有时比平均速度大，有时比平均速度小.当然，匀速运动的情形两者相等.

总体均值在某两个局部均值之间，这是平均值的基本属性.如果全班的一次考试成绩平均80分，一定有高于80分的同学，也有低于80分的同学，除非人人都是80分！

如果你刚才没有想到这一点，可能是因为它太平凡太简单了.数学家几百年来都忽略了这个平凡的道理.你如果想不到也很正常.

如果想到了这一点，祝贺你！走向微积分殿堂的另一条通道在你面前打开了.

把这个想法用于（1－1）式，在a＝1时，看出平均速度u＋v满足不等式

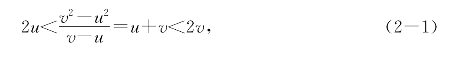
也得到了表达式2u或2v！

在（2－1）中没有任何可怀疑之处.但作为一个数学方法，它的严谨性和有效性有待检验.毕竟（1－3）经历过几个世纪的风风雨雨，而（2－1）则是呱呱落地的柔弱的婴儿！

从平凡的（2－1）出发如何继续前进？它和牛顿的天才思路（1－3）有什么联系？这是我们要继续思考探索的问题.

把原始的思路提炼成数学语言，才能深入，才能发展.

对于非匀速运动，“瞬时速度有时比平均速度大，有时比平均速度小”.用数学语言如何表达这个想法呢？

仍用函数S＝S（t）表示运动方程，设时刻t的瞬时速度为V（t）.于是，“瞬时速度有时大于等于平均速度，有时小于等于平均速度”.用数学语言来表达，就是

在[u，v]上有点p和q满足不等式

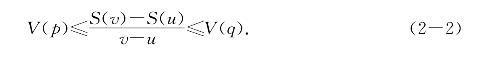
注意，我们现在还不知道瞬时速度的数学定义.但从物理直观看来，运动物体有瞬时速度，并和平均速度之间有上述关系，

不等式（2－2）中用“小于等于”的不等号，这把匀速运动的情形也包括在内了.

这个不等式描述的是两个函数S（t）和V（t）之间的关系.举一反三，把概念一般化，得到下面的定义.

定义2 （甲函数和乙函数）设函数F（x）和f（x）都在数集S上有定义，若对S中的任意两点u＜v，总有[u，v]∩S中的p和q，使有不等式

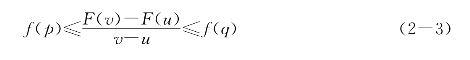
成立，则称F（x）是f（x）在数集S上的甲函数，f（x）是F（x）在数集S上的乙函数（注意在（2－3）中不排斥p＝q的情形）.

用不等式（2－3）可以估计F（x）的差商，故称“估值不等式”.

通常数集S是某个区间，但在定义中不限于区间，例如，数集S可能是有理数集或正整数集.

如图2－1，在函数y＝F（x）的曲线上取两个点A＝（u，F（u））和B＝（v，F（v））.如前所述，割线AB的斜率是F（x）在[u，v]上的差商.设曲线上横坐标x＝p的点E处的切线的斜率为k（p）.直观上看k（p）有时大于割线的斜率，有时小于割线的斜率.把切线的斜率看成切点横坐标x的函数k＝k（x），按定义它是y＝F（x）的乙函数.

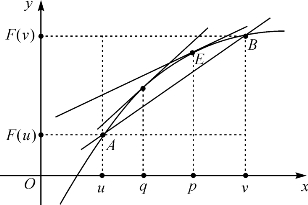
图2－1　割线斜率在两切线斜率之间

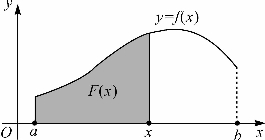
图2－2　曲线下面积随x变化构成函数

再看图2－2.将函数f（x）的曲线和x轴之间在[a，x]上方的这块曲边梯形面积记作F（x）.则图2－3中[u，v]上这块曲边梯形面积为F（v）－F（u）.如果把这块曲边梯形面积去高补低折合成长为v－u的矩形，则矩形的宽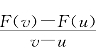应当在f（x）在[u，v]上的某两个函数值f（p）和f（q）之间.这表明f（x）是F（x）的乙函数.

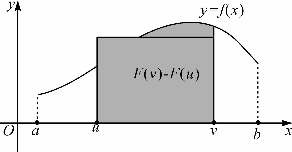
图2－3　矩形的高在f(x)的某两个函数值之间

从这些直观描述的例子看，甲乙函数的概念不但有鲜明的物理意义，而且有丰富的几何意义.

从数学本身看，不等式（2－3）提供了估计函数F（x）的差商的手段，函数的性质和差商有密切关系.差商为0，F（x）就是常数；差商为非零常数，F（x）就是一次函数；差商为正，则F（x）递增；差商为负，则F（x）递减；差商非正，则F（x）不增；差商非负，则F（x）不减；掌握了差商的性质，对函数的性质也就了若指掌.但是差商的表达式涉及两个变元，一般说比较复杂.如果能够用较为简单的一元函数来估计差商，当然很好.这个用来估计F（x）的差商的函数，就是F（x）的乙函数.

乙函数如此重要，下面就来尝试计算常见函数的乙函数.

命题2.1 求常数函数f（x）＝C的一个乙函数.

证明 对[u，v]上任两点p和q总有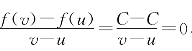，所以恒为零的函数是常数函数f（x）＝C的一个乙函数.

命题2.2 求一次函数f（x）＝k·x＋C的乙函数.

证明 对[u，v]上任两点p和q总有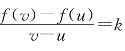，即常数函数c（x）＝k是f（x）＝k·x＋C的乙函数.

命题2.3 （i）若E（x）是f（x）在S上的乙函数.对任意常数a、k和C取g（x）＝a·f（x）＋k·x＋C，则a·E（x）＋k是g（x）的乙函数；

（ii）若E（x）是f（x）在S上的乙函数.对任意常数C取g（x）＝f（x＋C），并记S1＝{x|x＋C∈S}，则E（x＋C）是g（x）在S1上的乙函数；

（iii）若E（x）是f（x）在S上的乙函数.对任意k≠0取g（x）＝f（k·x），并记S1＝{x|k·x∈S}，则k·E（k·x）是g（x）在S1上的乙函数.

证明 （i）因E（x）是f（x）在S上的乙函数，对S中的任意两点u＜v，总有[u，v]∩S中的p和q，使有

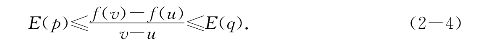
将（2－4）乘以a再加k，当a≥0时有

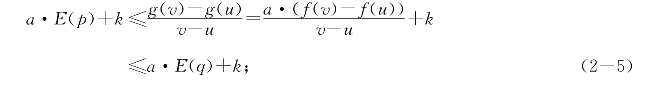
当a≤0时有

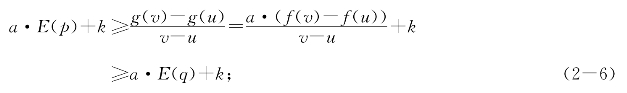
按定义a·E（x）＋k是g（x）的乙函数.

（ii）对S1中任意两点u＜v，记u1＝u＋C和v1＝v＋C，则u1和v1在S中，故有[u1，v1]∩S中的两点p1和p2使E（p1）≤≤E（q1），记p＝p1－C和q＝q1－C，注意到f（v1）＝f（v＋C）＝g（v）和f（u1）＝f（u＋C）＝g（u），便得

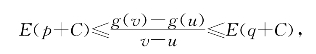
这证明E（x＋C）是g（x）在S1上的乙函数.

（iii）类似于（ii），对S1中任意两点u＜v，记u1＝k·u和v1＝k·v，则u1和v1在S中，故有[u1，v1]∩S（或[v1，u1]∩S，视k为正或负而定）中的两点p1和p2，使E（p1）≤≤E（q1），记和，注意到f（v1）＝f（k·v）＝g（v）和f（u1）＝f（k·u）＝g（u），便得

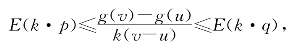
从而在k·E（k·p）与k·E（k·q）之间，这证明k·E（k·x）是g（x）在S1上的乙函数.

命题获证.

在上述命题中取特款和简单推论，得到常用的求乙函数的法则：

命题2.4 （i）若f（x）－g（x）为常数，则g（x）和f（x）有相同的乙函数；

（ii）若E（x）是f（x）的乙函数，g（x）＝a·f（x）而a为常数，则a·E（x）是g（x）的乙函数；

（iii）若E（x）是f（x）在S上的乙函数，g（x）＝f（k·x＋C）而k≠0，S1＝{x|（k·x＋C）∈S}，则k·E（k·x＋C）是g（x）在S1上的乙函数.

命题2.5 求f（x）＝x2的乙函数.

证明 令g（x）＝2x，p＝q＝∈[u，v]，则

这表明g（x）＝2x是f（x）＝x2的乙函数.

当然，也可以取p＝u和q＝v，由2u＜u＋v＜2v表明g（x）＝2x是f（x）＝x2的乙函数.

命题2.6 在（－∞，0）和（0，＋∞）上求f（x）＝的乙函数.(www.daowen.com)

证明 当0＜u＜v时有

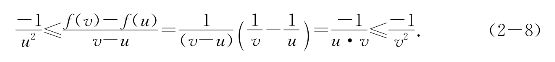
取p＝u和q＝v可见g（x）＝－是f（x）＝在（0，＋∞）上的乙函数；

当u＜v＜0时有

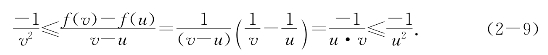
取p＝v和q＝u可见g（x）＝－是f（x）＝在（－∞，0）上的乙函数.

命题2.7 求f（x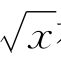）＝在（0，＋∞）上的乙函数.

证明 计算f（x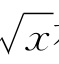）＝在正数u＜v处的差商得

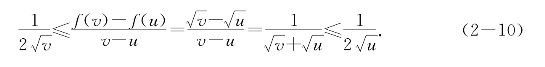
取p＝v和q＝u可见g（x）＝是f（x）＝在（0，＋∞）上的乙函数.

命题2.8 数列an＝a（n）（n＝0，1，2，…）可以看成定义域为自然数集的函数，其前n＋1项之和也是定义域为自然数集的函数.则a（n）是S（n）的乙函数.

证明 对于任意两个自然数n＜m，有

设{an，an＋1，…，am}中最小者为ap，最大者为aq（两者可能相等），则

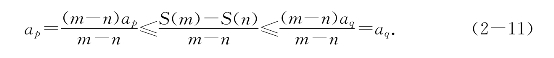
这表明a（n）是S（n）的乙函数.

命题2.9 设g（x）是f（x）在S上的乙函数，u＜v是S中的两点，则有

（i）若g（x）在[u，v]∩S上恒为0，则f（x）在[u，v]∩S上为常数；

（ii）若g（x）在[u，v]∩S上为常数k≠0，则f（x）在[u，v]∩S上为一次函数k·x＋C；

（iii）若在[u，v]∩S上有g（x）＞0，则f（x）在[u，v]∩S上递增；

若在[u，v]∩S上有g（x）≥0，则f（x）在[u，v]∩S上不减；

（iV）若在[u，v]∩S上有g（x）＜0，则f（x）在[u，v]∩S上递减；

若在[u，v]∩S上有g（x）≤0，则f（x）在[u，v]∩S上不增.

证明 （i）由条件推出f（x）在[u，v]∩S上差商为0，故为常数；

（ii）由条件推出f（x）在[u，v]∩S上差商为k，即对x∈[u，v]∩S有，从而f（x）＝k·（x－u）＋f（u）；

（iii）由[u，v]∩S上g（x）＞0和估值不等式推出f（x）在[u，v]∩S上差商为正，故递增；

由[u，v]∩S上g（x）≥0和估值不等式推出f（x）在[u，v]∩S上差商非负，故不减；

（iV）由[u，v]∩S上g（x）＜0和估值不等式推出f（x）在[u，v]∩S上差商为负，故递减；

由[u，v]∩S上g（x）≤0和估值不等式推出f（x）在[u，v]∩S上差商非正，故不增.

将命题2.1到2.7和命题1.1到1.7顺次对比，不难发现乙函数和导数的相似之处.特别是对于函数来说，乙函数和导数完全相同！

但乙函数和导数又不是完全相同：

第一，函数F（x）的导数是在一点x＝u处定义的，并要求F（x）在包含x＝u的某个区间上有定义；而F（x）的乙函数是在F（x）的定义域数集S上定义的，S可以不包含区间，如命题2.8；

第二，导数的定义中用到了暂时还说不清楚的自然语言，难以作为严谨推理的基础，乙函数的定义是严谨的数学语言；

第三，由命题2.9可见，根据F（x）的乙函数的性质很容易推出F（x）的性质；而从F（x）的导数的定义却很难看出F（x）的性质，要用导数研究函数，需要作更深入的研究；

第四，按定义求函数的乙函数过程很清楚，按定义求函数的导数要借助于直观，费更多的口舌.

“导数正则函数增”是常用的命题，但不容易证明；“乙函数正则函数增”却非常显然！

到此为止，新方法的优势很明显，这样简单的思路在数学发展的悠长岁月里居然没有被发现，是值得深思的有趣的事情！

例题2—1 求f（x）＝在（0，＋∞）上的乙函数g（x），作两个函数的图象，并利用g（x）的性质研究f（x）的增减性.

解 应用命题2.6和2.3可知g（x）＝是f（x）的乙函数.当0＜x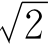＜时g（x）＜0，当x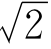＞时g（x）＞0，由命题2.9可知，f（x）在（0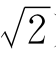）递减，在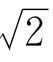（，＋∞）递增.如图2－4.

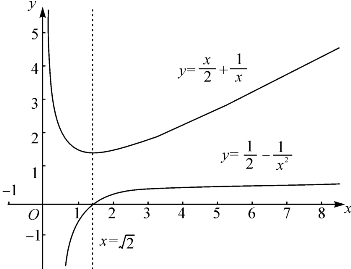
图2－4　用乙函数的正负判断函数增减

例题2—2 利用命题2.7求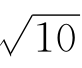的近似值.

解 在不等式（2－10）中取v＝10和u＝9得到

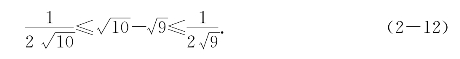
由此得到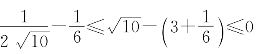，如果取3＋≈3.167作为的近似值，从不等式可知此近似值是过剩近似值，且误差不会超过

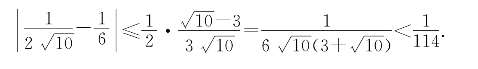
和例题1－2比较，这里的推理更清楚，而且还能够估计近似值的误差.

习题2—1 求f（x）＝4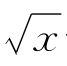－x在（0，＋∞）上的乙函数g（x），作两个函数的图像，并利用g（x）的性质研究f（x）的增减性.

习题2—2 利用命题2.1至2.7求下列函数的乙函数.

（i）y＝5－7x＋2x2；

（ii）f（x）＝－4x＋3（x≠0）；

（iii）g（x）＝5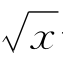－3x＋6（x＞0）；

（iV）y＝2cos2x－cos2x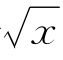＋＋1（x＞0）.

习题2—3 试用定义求G（x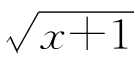）＝（x≥－1）的乙函数.

习题2—4 试用定义求f（x）＝（x≠－1）的乙函数.

习题2—5 模仿例题2－2，取u＝10和来求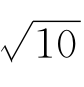的近似值，并估计其误差.

习题2—6 设有三个定义于自然数集合上的函数a（n）＝2n＋1，b（n）＝2n＋2和S（n）＝n2＋2n＋4，根据定义证明a（n）和b（n）都是S（n）的乙函数.

习题2—7 符号函数sgn（x）的定义为

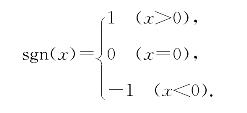
试证明它是A（x）＝|x|的乙函数.

习题2—8 设g（x）是f（x）在区间I上的乙函数，u＜v是I中的两点，求证：

（i）若g（x）在（u，v）上恒为0，则f（x）在[u，v]上为常数；

（ii）若g（x）在（u，v）上恒为常数k≠0，则f（x）在[u，v]上为一次函数k·x＋C；

（iii）若在（u，v）上有g（x）＞0，则f（x）在[u，v]上递增；

（iV）若在（u，v）上有g（x）＜0，则f（x）在[u，v]上递减.

【关于乙函数的一个注记】 是不是在区间I上定义的每个函数都有乙函数呢？回答是肯定的.请看下面的例子.

在每个区间上无上界也无下界的函数 在区间I上定义函数f（x）：若x为无理数，令f（x）＝0；若x为既约分数（p＞0），令f（x）＝（－1）p·p.则容易证明，f（x）在任意长度不为0的区间上既无上界也无下界.

显然，这样定义的函数f（x），它是在区间I上定义的每个函数的乙函数！这样的乙函数无助于了解它的甲函数.所以下面要对乙函数加上某些限制，使它规规矩矩地为我们服务.