有句古话，叫做“强弩之末势不能穿鲁缟”.字面上是说射出的箭尽管开始很有力，也就是很快，但后来速度会慢下来，到了射程之末连细绢也穿不透了.当然，这是由于空气阻力的作用.

其实，强弩之末速度到底如何，还要具体分析.如果从高高的城门楼上射下来，像三国演义里陈宫向曹操射的一箭，由于重力，箭会越来越快；如果从下向上“弯弓射大雕”，初速再大，也会越高越慢；到了最高处回头下落，又会越来越快.

总之，箭的运动速度时时刻刻在变化，这在物理上叫做非匀速运动.求非匀速运动物体每时每刻的速度，是物理学家关心的问题.

意大利物理学家伽利略（G.Galilei，1564—1642）研究了重力作用下物体的运动规律.他经过反复实验，总结出小球在光滑斜面上滚下的距离S和所用的时间t之间有函数关系S＝S（t）＝at2，这个式子叫做小球的运动方程.其中系数a和斜面坡度以及计量单位有关.

有了运动方程，在时间段[u，v]上小球滚过的距离很好算，就是S（v）－S（u）＝av2－au2.滚过这段距离的时间是v－u，于是在时间区间[u，v]上小球的平均速度就是

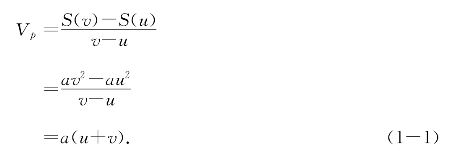
知道了任意时间段上的平均速度，如何求任一时刻的速度，即所谓瞬时速度呢？

伽利略没能解决这个问题.他遭遇到了概念上的困难.

要算速度，就要知道物体在一段时间走过的距离.只看一个时刻，时间和走过的距离都等于0，通常的速度概念失去了意义！

英国科学家牛顿（IsaacNewton，1642—1727）设想，如果在（1－1）中让时刻v越来越接近u，即让时间区间缩小到非常非常接近于0，则右端的a（u＋v）越来越接近2au.所以时刻t＝u的瞬时速度应当是2au.

例如，自由落体开始下落t秒时经过的距离为，即a＝，这里g＝9.8（m/s2）是重力加速度，易算出下落3秒时其瞬时速度为29.4（m/s）.这和物理学中按能量守恒定律算出来的结果一致.

为了强调要计算的是时刻t＝u处的瞬时速度，记v－u＝h，从而v＝u＋h，于是（1－1）成为

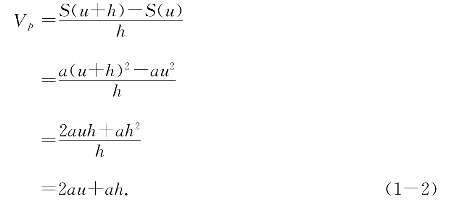
从上面的等式容易看出，不论h是正是负，当它无限接近于0时，平均速度Vp就会无限接近于2au.因此，认为2au是时刻t＝u的瞬时速度，直观上看是合理的.

能不能简单点，干脆在（1－2）中取h＝0呢？仔细看看，不行！原来h在等式中还要充当分母，所以不能为0，只能接近于0.多么接近于0都可以，就是不能等于0.

“当h无限接近于0时，就会无限接近于2au”这句话，用现代数学的极限符号表示，就是

这个式子读作“当h趋于0时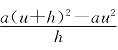，的极限为2au”，或简单地说“当h趋于0时趋于2au”.

牛顿这样得出的答案，数学上不够严谨，当时引起了怀疑和争论.

怀疑这个方法的人问：让h无限接近0，接近到什么程度呢？如果h≠0，就只能得到平均速度而非瞬时速度；如果h＝0，以它为分母的分式就失去了意义！

在长达150多年间，数学家说不清极限概念，无法回答质疑.

尽管道理说不清，一大批出色的数学家仍然沿着牛顿的思路前进，解决了科学技术中提出的大量问题，取得了辉煌的成果.

直到19世纪20～70年代，经过柯西（A.L.Cauchy，1789—1851）、魏尔斯特拉斯（K.Weierstrass，1815—1897）、戴德金（R.Dedekind，1831—1916）、康托（G.Cantor，1845—1918）等一批卓越的数学家的工作，才建立了严谨的极限概念和理论，为微积分打下了坚实的数学基础.

运动方程S（t）是一般函数f（x）的特例.举一反三，把平均速度的表达式里的路程S（v）和S（u）换成一般函数值f（v）和f（u），得到的比值叫做f（x）在区间[u，v]上的“平均变化率”，这是我国近年来中学教材上的说法.按国内外数学书刊上通常的术语，这个比值叫做函数f（x）在u和v两点的“差商”（quotientofdifference）.这个词不但简单，而且具体明确：它是两点处函数值的差除以自变量的差所得的商.有些书上差商也叫“增量比”，所谓增量就是差，比就是商.

在y＝f（x）的曲线上取两点A（u，f（v））和B（v，f（v）），差商就是直线AB的斜率，如图1－1.

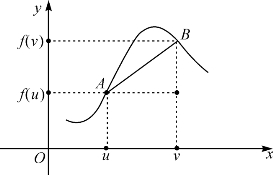
图1－1　差商的几何意义

将牛顿关于瞬时速度的想法一般化，引出一个重要的定义.

定义1 设函数y＝f（x）在包含点u的某个区间上有定义.如果在h趋于0的过程中差商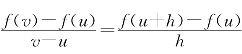趋于一个确定的数A，这个数就叫做函数f（x）在点x＝u处的微商或导数，记作f′（u）＝A或y′|x＝u＝A，并且称f（x）在点x＝u处可导；f′（u）＝A也叫f（x）在点x＝u处的瞬时变化率.

如果y＝f（x）在区间I的每个点x处都有导数f′（x），称f（x）在区间I可导或点点可导，这时f′（x）（简单记作y′）也是在区间I上有定义的函数，也叫做f（x）在区间I上的导函数，用极限记号表达为

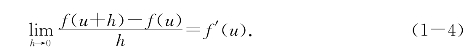
简单地说，当分母趋于0时若差商有极限，这极限叫做导数.

差商的分母v－u是函数y＝f（x）的自变量的改变量，常记作Δx，分子f（v）－f（u）是函数值的改变量，常记作Δy，所以差商常常用符号表示.微积分早期的数学家认为，Δy和Δx在取极限的过程中分别转化为dy和dx，所以也用或表示导数f′（x）.现在，记号dy和dx已经有了更严谨准确的含意，如后面第12讲所述.

下面试试来算几个函数的导数.

命题1.1 常数函数f（x）＝C的导数为0，即C′＝0.

这是因为其差商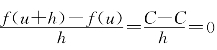，当h趋于0时它保持为0，即无限接近于0.注意，当我们说“当h趋于0时趋于数a”时，h不能等于0而可以等于数a.也就是说，两个“趋于”含意有所不同.前一个“趋于”含意是无限接近但不等于，后一个“趋于”含意是无限接近但不排斥等于的可能.道理很清楚，因为h承担了分母的任务.(www.daowen.com)

命题1.2 一次函数f（x）＝k·x＋c的导数为常数k，即（k·c＋C）′＝k.

证明 差商

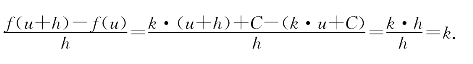
可见当h趋于0时它保持为k，即无限接近于k.

命题1.3 对任意常数a、k和C取g（x）＝a·f（x）＋k·x＋C，则当f（x）可导时g（x）也可导，且

证明 计算g（x）的差商可得.当h趋于0时趋于f′（x），故左端趋于a·f′（x）＋k.

在上述命题中取特款，得到两个常用的计算导数的法则.

命题1.4 （i）若f（x）－g（x）为常数，则g′（x）＝f′（x）；

（ii）若g（x）＝a·f（x），而a为常数，则g′（x）＝a·f′（x）.

命题1.5 在（－∞，＋∞）上有（x2）′＝2x.

这是前面求瞬时速度时计算过的题目，温习一下.

命题1.6 当x≠0时，有.

证明 计算f（x）＝在x＝u≠0和u＋h≠0处的差商得

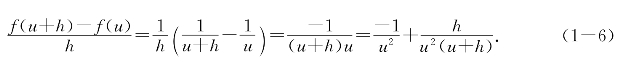
当h趋于0时右端是不是趋于呢？这一眼看不出来.当|h|很小很小时，右端的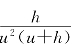是不是非常非常接近于0呢？你如果直观上相信当h趋于0时右端确实趋于，就跳过下面的分析去看下一个命题.如果怀疑，就仔细看看.

比如，当|h|很小很小时，能不能使得＜0.001呢？

若|h|小得满足|h|＜|0.2u|，则|u＋h|＞|0.5u|，从而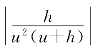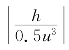＜.想要＜0.001，只要|h|＜|0.0005u3|和|h|＜|0.2u|同时成立即可.

类似推理可知，只要|h|足够小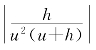，还可以小于0.0001，小于0.0000001，小于0.0000000001，总之要多小就能够有多小.

命题1.7 当x＞0时，有.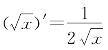

证明 计算f（x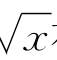）＝在x＝u＞0和u＋h＞0处的差商得

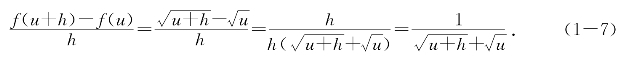
当h趋于0时右端趋于，命题得证.

如果不相信，辛苦一下详细写出

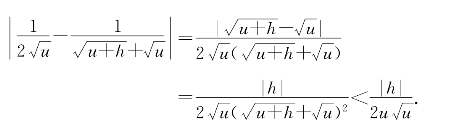
这就真相大白了.

例题1—1 求二次函数y＝x2－5x＋6的导数，并在一个坐标系中作出此函数及其导函数的图像.

解 应用命题1.5和1.3得到y′＝2x－5，图像如图1－2.

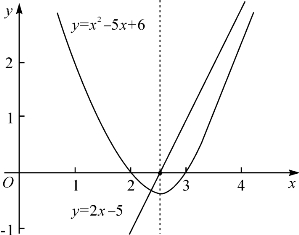
图1－2　二次函数及其导函数图象

例题1—2 利用命题1.7的结果，求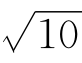的近似值.

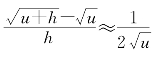解 命题1.7的结果为.由于当h接近0时差商接近导数，故.取u＝9和h＝1得，于是得≈3.167.

习题1—1 应用命题1.1至1.7，计算下列函数的导数，并作出各函数及其导数的图像.

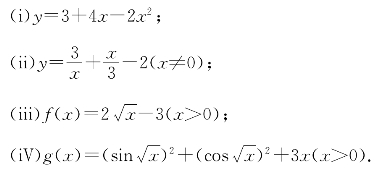
习题1—2 利用命题1.7的结果估计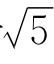的近似值.