对于前面讲到的一些问题，我们似乎都是从经济学的角度来分析的。如买地的问题，巴霍姆付出了一定的努力，到底怎样做，得到的土地才最多呢？这其实就是怎样才能在付出后得到最大利益的问题。

该类问题有一个专有名词，即“极大值和极小值”。它们的类型多种多样，解答时难易程度也不一样，有的甚至要借助高等数学的帮助，还有一些比较简单，只需普通的数学知识就行了。接下来，我们再来讨论几个类似问题，它们会用到几何学上的另一个内容，即定和乘数的乘积。

我们已经知道，两个和一定的数，它们的乘数和乘积具有一些通用的性质。比如，在周长相等的情况下，正方形的面积大于矩形的面积。将其换成算术上的说法，就是：若将一个数分成两部分，并使它们的乘积最大，则应该将这个数进行二等分。诸如，在以下一些数的乘积中：17×13、16×14、18×12、19×11、20×10、15×15，每组中两个数的和都是30，但乘积最大的是15×15。

若换成3个数，也就是说，只要3个数的和一定，前面的性质仍然适用。实际上，根据前面的内容，我们可以得出这个性质。假设有3个数x、y和z，它们的和为a，即

x+y+z=a

不妨假设x不等于y，若将这两个数分别用其和的一半来表示，则3个数的总和不变，即(www.daowen.com)

由之前的推论，我们得出

因此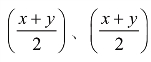，、z的乘积大于x、y、z的乘积，即

综上所述，若x、y、z这3个数中有两个不相等，我们一定能在保证它们的和不变的情况下，找出一组数比它们的乘积更大。意思就是，只有这3个数相等时，这种可能才彻底被排除。因此，若x+y+z=a，那么只有在下列条件下，3个数的乘积xyz才是最大的：

x=y=z

接下来，根据这一特性，我们来解决几个特别有趣的问题。