新的问题又来了，若巴霍姆走出的不是矩形，而是其他形状，如三角形、四边形或五边形，得到的土地会不会更多？

针对这个问题，我们也可以进行严格的数学分析，但是估计读者朋友们已经非常厌烦了，所以还是直接告诉大家结果吧。

前文中，我们已经证明，在周长相等的矩形中，面积最大的是正方形。实际上，不光是矩形，在所有周长相等的四边形中，面积最大的也是正方形。因此，假设巴霍姆一天可以跑40俄里，倘若他想获得一块四边形的土地，则这块土地的面积一定小于100平方俄里。

除此之外，我们还可以证明：正方形是所有与它的周长相等的三角形中的面积最大的。若正方形的周长为40俄里，则假设a为正三角形的边长，与正方形周长相等的等边三角形的边长就是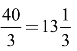（俄里），因此它的面积为

也就是说，该三角形的面积小于那个梯形。后面，我们会接着证明，在所有周长相等的三角形中，面积最大的是等边三角形。因此，若这个最大面积都比正方形的面积小，便可以断定，其他周长相等的三角形一定也比正方形的面积小。

但是，倘若将正方形与周长相等的五边形、六边形进行比较，正方形的这一优越性就会荡然无存。我们可以证明，周长相等的正五边形的面积比正方形的面积大，正六边形的面积更大。(www.daowen.com)

下面，我们以一个正六边形为例进行证明。若周长还是40俄里，则这个正六边形的边长为

假设a为正六边形的边长，它的面积为

倘若巴霍姆走出的是正六边形，则他在付出相同体力的前提下，获得的土地会增加115-78=37（平方俄里），会比正方形路线多出15平方俄里。当然了，如果选择这种路线，他可能还要带一个测角仪之类的工具。

【问题】用6根火柴，摆出一个面积最大的封闭路线。

【解答】实际上，用6根火柴能够摆出很多种路线，有正三角形、矩形、平行四边形、不等边的五边形、不等边的六边形、正六边形等。但对一个“几何学家”而言，他一眼就可以分辨出哪种图形的面积最大，那就是正六边形。