【问题】巴霍姆为了得到更多的地，最后竟然连命都没了。那么，他到底走了多远呢？实际上，这个数值很容易就能够计算出来，为10+13+2+15=40（俄里）。

巴霍姆走出的路线是一个梯形，他原本想走出一个矩形，结果却走成了梯形，这是因为事先没有算好。走出来的这个梯形和矩形相比，哪个对他更有利呢？这个问题很有趣。他走什么形状，才能获得最多的土地呢？

【解答】若一个矩形的周长为40俄里，它的形状可以有很多种，每种的面积都不一样。比如，可以有以下几种情况：

假如边长分别为14和6，则面积为14×6=84（平方俄里）。

假如边长分别为13和7，则面积为13×7=91（平方俄里）。

假如边长分别为12和8，则面积为12×8=96（平方俄里）。

假如边长分别为11和9，则面积为11×9=99（平方俄里）。(www.daowen.com)

从上面的几种情况能够得出，虽然各种矩形的周长相等，面积却各不相同。不过，它们的面积都比梯形大。若矩形的周长为40俄里，面积小于刚才的梯形的情况也存在：

假如边长分别为18和2，则面积为18×2=36（平方俄里）。

假如边长分别为19和1，则面积为19×1=19（平方俄里）。

假如边长分别为和，则面积为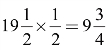（平方俄里）。

因此，对于第一个问题，我们无法作答。周长相等时，有些矩形面积大，有些梯形面积大。但是对于第二个问题，我们完全可以作出解答。也就是说，若矩形的周长相等，一定能找出一个面积最大的来。

若将前面列出来的每个矩形进行比较，我们就会看出，矩形的两个边长差距越小，面积就越大。因此可以下结论：当两边的差距为0时，该矩形的面积最大。这意味着当矩形变成正方形时，面积最大。因此，只有走出一个正方形，巴霍姆得到的土地才最多，会比他在故事中走出的多出22平方俄里。