小学课本里通常会有一个故事，与一只聪明的乌鸦有关。这个故事是这样的：有一只乌鸦，它在口渴的时候找到一个细瓶子，但是瓶子里的水不多，它的嘴又没有办法伸进瓶子里。最后，乌鸦想到一个好办法，找了一些小石头，将它们扔进瓶子里。结果，瓶子里的水升高了，它喝到了水。

这里，我们没有必要去讨论这只乌鸦是否真的如此聪明，我们感兴趣的只是故事中的几何学知识。我们来看下面的问题。

【问题】假设瓶子里水的高度恰好为瓶子的一半，这只乌鸦能否喝　到水？

【解答】通过解答这个问题，我们会知道，如果采用乌鸦的方法，并不是任何水量的水都能喝到。

为了使问题更简单，我们假设这个瓶子的形状为方柱体，投进去的石头都是大小相同的球体，则不难得出，瓶子里水的体积大于投进瓶子里的石头空隙的体积，只有这样，瓶子里的水才会没过石头。也就是说，水会把石头的空隙全部填满，并且剩下多余的一部分，可以没过石头。

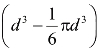接着，我们来计算一下，这些空隙究竟占了多大体积。要想计算空隙的体积，最简便的方法是假设每块石头的圆心正好在一条竖直线上，换句话说，石头上下垂直摆放在一条直线上。假设每块石头的直径为d，则它的体积为，而跟它外切的立方体的体积为d3，它们的差为，即这个外切立方体中没有被石头占据部分的体积。它们的比值为：(www.daowen.com)

由此可知，在每个外切立方体中，没有被石头占据部分的体积占整个体积的48%。也就是说，瓶子里面所有空隙体积的总和，小于瓶子容积的一半。如果瓶子不是方柱体，石头也不是球形，对答案不会产生任何影响。无论在什么情况下，我们都可以肯定一点，如果瓶子里最开始的水量不到瓶子容积的一半，那么不管这只乌鸦投多少石头，瓶子里面的水都不可能升到瓶口。假设这只乌鸦足够聪明，它会摇动瓶子，使里面的石块挨得更紧，水面完全有可能升高到原来的2倍，但这根本不可能。因此，最符合实际的情况就是，石头堆积得比较松散，而且，通常而言，盛水的瓶子都是中间粗，两头细，水面升高的程度就会降低。所以，我们几乎可以肯定地说，如果瓶子里的水只是一小半，乌鸦再聪明，也不可能喝到瓶子里的水。

【注释】

[1]阿基米德（公元前287—前212年），古希腊哲学家、数学家和物理学家。

[2]杰克·伦敦（1876—1916年），美国著名的现实主义作家，代表作品有《马丁·伊登》和《野性的呼唤》等。

[3]1英亩≈4 046.856平方米。