【摘要】:但在古时候,就算是埃及祭司或罗马帝国最杰出的建筑师,也很难精确地计算出圆的周长。当时,埃及人认为圆的周长为直径的3.16倍,罗马人则认为应该是3.12倍。与后来的数学家不同,当时的数学家们并不是利用几何学知识进行计算的,而完全根据经验来计算。由此可以看出,与3.14相比,通过该方法得到的π值存在的误差还真不小,可能是3.1或3.12,或者是3.17。当然了,也有可能正好是3.14,不过,与其他的值一样,这个值并没有引起测量者的特别关注。
现在,连初中生都知道用直径来计算圆的周长。但在古时候,就算是埃及祭司或罗马帝国最杰出的建筑师,也很难精确地计算出圆的周长。当时,埃及人认为圆的周长为直径的3.16倍,罗马人则认为应该是3.12倍。现在我们都知道这个倍数其实是3.141 59…。
与后来的数学家不同,当时的数学家们并不是利用几何学知识进行计算的,而完全根据经验来计算。那么,为什么会产生那么大的误差呢?其实,这个比例关系很容易得到。只要把一根丝线缠绕在圆形物体上,再将它的长度和这个圆形物体的半径测量出来,问题就解决了。
实际上,他们是这样做的,是不是觉得很简单?但你知道吗?这样得到的结果可能并不准确。大家知道,如果一个圆瓶的直径为100毫米,其圆周的长度就等于314毫米。不过,在用细线测量时,得到的结果并不一定是这样,1毫米的误差已经非常小了。若真的存在1毫米的误差,算出来的π值就等于3.13或3.15。而且,还有一点,测量圆瓶的直径时也可能不太准确,往往会产生1毫米的误差。那么,这个π值就介于![]() 与
与![]() 之间,若表示成小数,则为3.0~3.18。(www.daowen.com)
之间,若表示成小数,则为3.0~3.18。(www.daowen.com)
由此可以看出,与3.14相比,通过该方法得到的π值存在的误差还真不小,可能是3.1或3.12,或者是3.17。当然了,也有可能正好是3.14,不过,与其他的值一样,这个值并没有引起测量者的特别关注。
通过这样的实验,根本不可能得出可使用的π值。说到这里,你应该明白了,古时候的人为什么得不到圆周长度跟直径的确切比值。而阿基米德[1]是通过思考,才确定了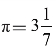 。
。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关趣味几何学的文章




