现在，已经总结了σ_es/RCS和其他形式的σ_es和RCS的研究。我们所说的关于σ_es/RCS的变化是针对最有可能的情况，但是其中的标签有可能发生在E和H很小的范围（当标签离基站距离很远），也有可能发生在E和H很大的范围（当标签离基站距离很近）。

事实上，如果要使其在很短和很长的范围内都可以正确应用的话，必须要在集成电路中引入一种名为“并联调节器”的新元素，以确保其在强磁场时节点端不会出现过高电压（见图3.6）。

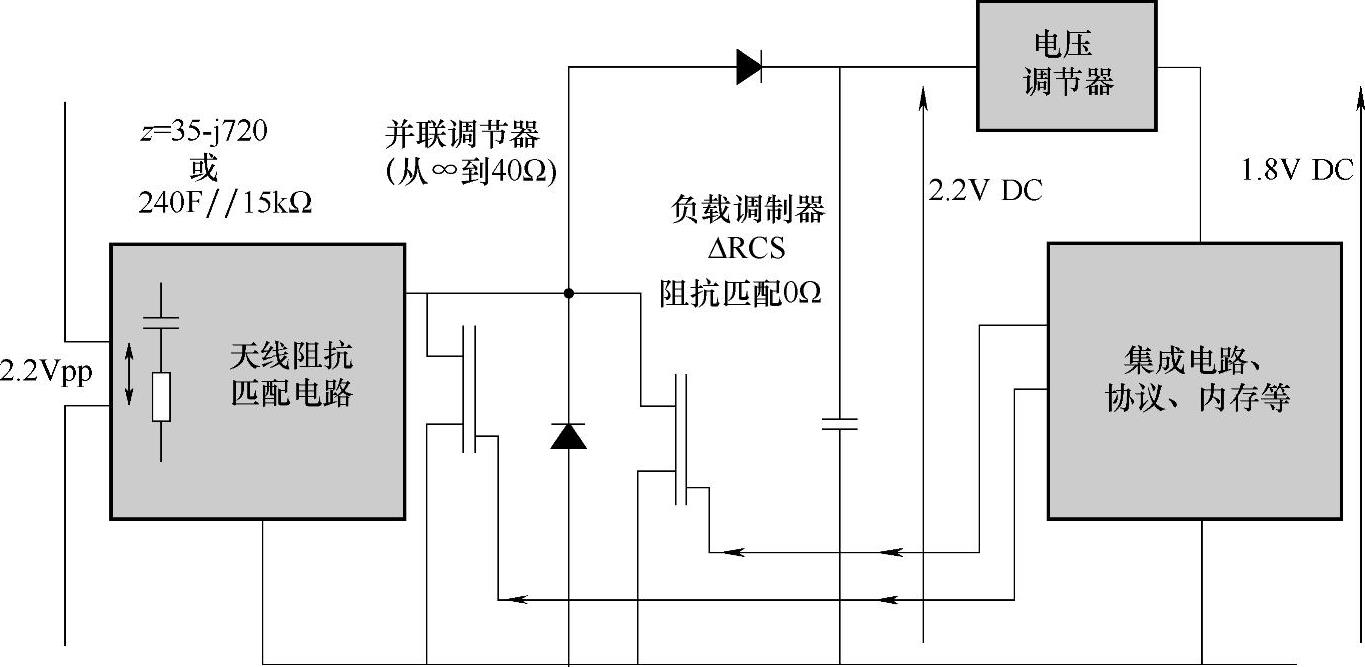
图3.6 UHF标签：框图（电路）

迄今为止所讨论的一切都与调节器处于非工作状态时的操作阶段有关，这很重要，因为它决定了系统的最大工作范围。当标签接近基站时，并联调节器迅速地进行集成电路并行输入的工作，从而当R_ant失配时就会引起参考点（设有调制处）的变化。因此，接近曲线的垂直轴，会使得ΔRCS的值比之前的小。这使得它更难保证在接近时操作ΔRCS的变化。

远程供电的标签问题是值得详细研究的（适用于大多数应用，因此主要以Γ₁=0），这将有助于我们了解RFID在UHF和SHF发生的现象。为了做到这一点，需要检查标签的真正的等效电路，同时也考虑其与基站之间距离所带来的影响。

1.标签离基站很远时

在这种情况下，标签没有接收到（捕获到）足够的能量以实现远程供电，所以未出现任何状况。

2.标签恰好在其运行的阈值（最大距离）

标签开始接收恰好是功率的最低数额（即阈值）。并联调节器没有进入工作状态（R_shunt无限大），也就意味着标签可以从所有来自基站的无线电波所供给的入射能量中获得能量（见图3.7）。

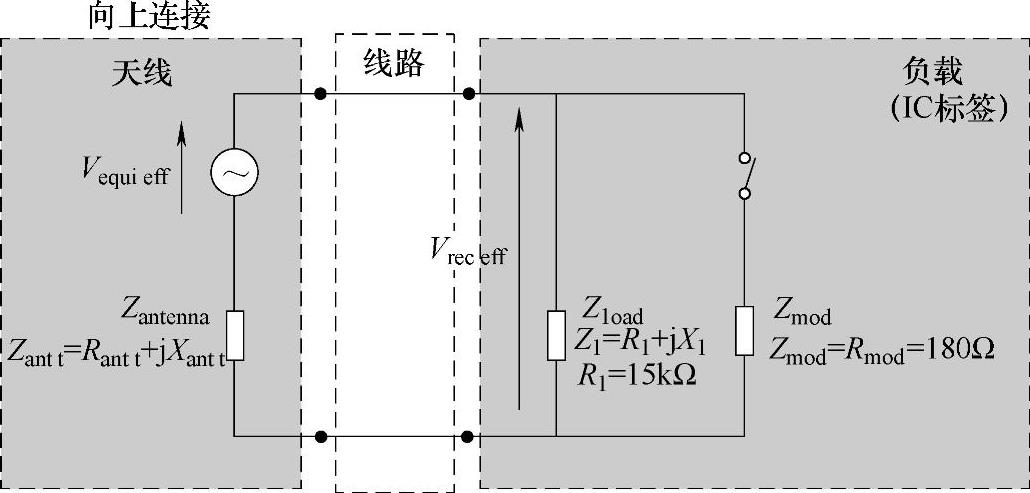
图3.7 阈值场中的标签

在远程供电标签的例子中，从“匹配”值（a_nonmod=R_l/R_antt=1）（以获得最大功率），到a_mod=（R_match‖R_mod/R_antt）的值，当数据需要从标签传送到基站时，“负载调制晶体管”会根据需要进入工作状态，同时调整负载阻抗，并移动标签天线，使初始的后向散射区域面积σ_structural增大到（σ_es/RCS），从而增强再辐射的入射波。图3.8总结了在弱磁场时ΔRCS的变化情况。

必须通过这种方法选择电阻R_mod，从而使基站能够解析通过标签发送的数据（以功率变化的形式），因此图中显示的ΔRCS的值一定高于最低水平。所以，R_modmax存在一个最大的欧姆值，α_mod和Γ_mod也是一样。下面给出了一种ISO1800-6（UHF）和1800-4（2.5GHz）标准下UHF的计算应用范例。换句话说，此时ΔRCS=50cm²（见下面案例）。

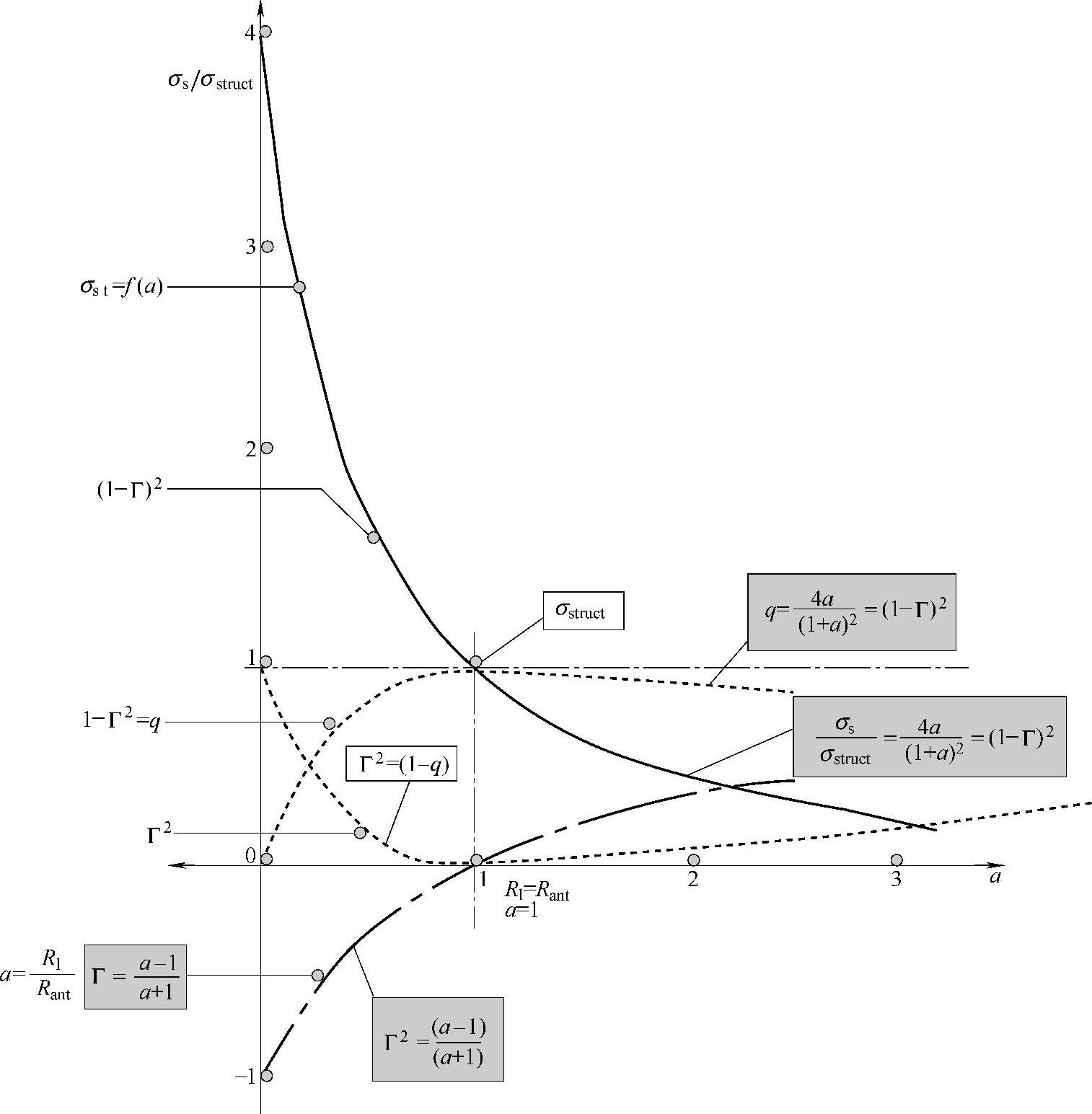
图3.8 ΔRCS在弱磁场下的变化情况

当然，可以考虑一种更简单的情况，就是当R_mod=0Ω时，立即提供区域ΔRCS最大可能的变化（见图3.9），假如这对于标签所消耗的能量没有影响，但是这是后话了，这里先不讨论。

3.范例：σ_es和在阈值范围内符合ISO18000-6

为了确保标签和基站的高度兼容性，ISO18000-6中“标签参数：7d”规定：“ΔRCS（不同的雷达散射的截面积）会影响系统的性能。典型数值大于0.005m²=50cm²”。也就是说，只要频率是在860～960MHz的频段范围（符合ISO 18000-6的强制要求范围）内，这个典型的最小值就是σ_es=50cm²。此外，考虑到σ_esstructural=0.214λ²，对于具有1.64增益的λ/2偶极子标签天线，此时可以计算出α的最小值α=R_l/R_antt。满足σ_es=50cm²。

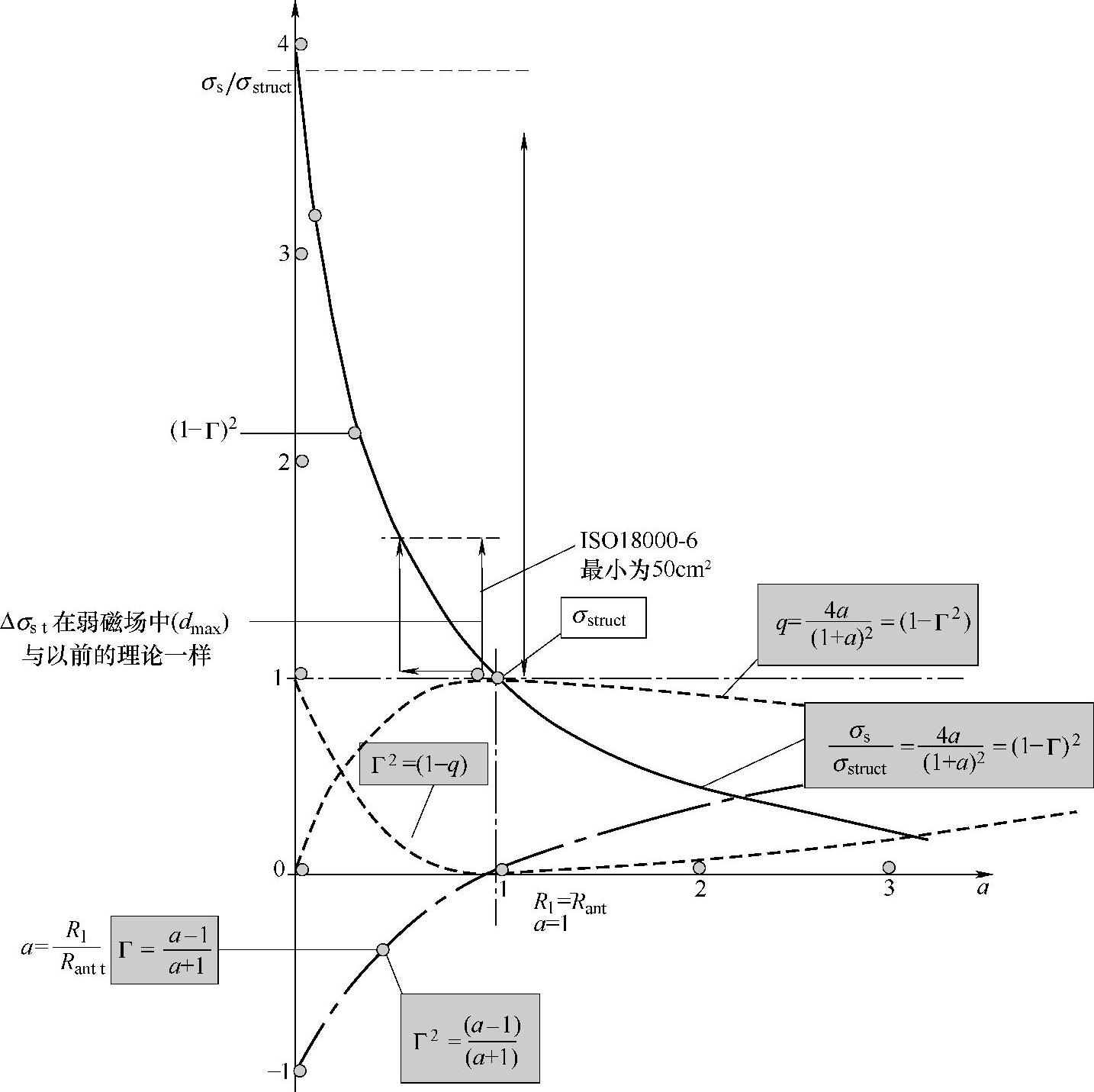
图3.9 优化变动的负载电阻使ΔRCS达到最高值

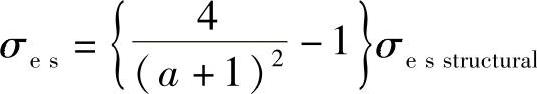
1）如果频率为960MHz，λ=0.3125m，σ_esstructual=209cm²，

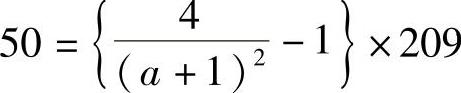
这种情况下：α=0.797。

2）如果频率为860MHz，λ=349m，σ_esstructual=260cm²，

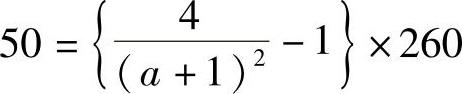
这种情况下：α=0.83。

这里R_antt=73.128Ω，R_l=αR_antt，在这种条件下，可以找到R_l的最小值的最大值。

情况1）下：R_lmin=58.28Ω，从而有Γ_min=-0.113；

情况2）下：R_lmin=60.7Ω，从而有Γ_min=-0.093。

注意：

当Γ_min非常低（大约-0.1时）的情况下，Γ有可能会达到0，因此

σ_es=-2Γσ_esstructural

代入得

σ_es=（-2）×（-0.1）×250=50cm²(www.daowen.com)

4.标签进入正常作业范围

现在标签被正常供电，甚至高于其严格要求的最低水平。并联调节器开始起作用，以限制集成电路的输入电压（见图3.10）。

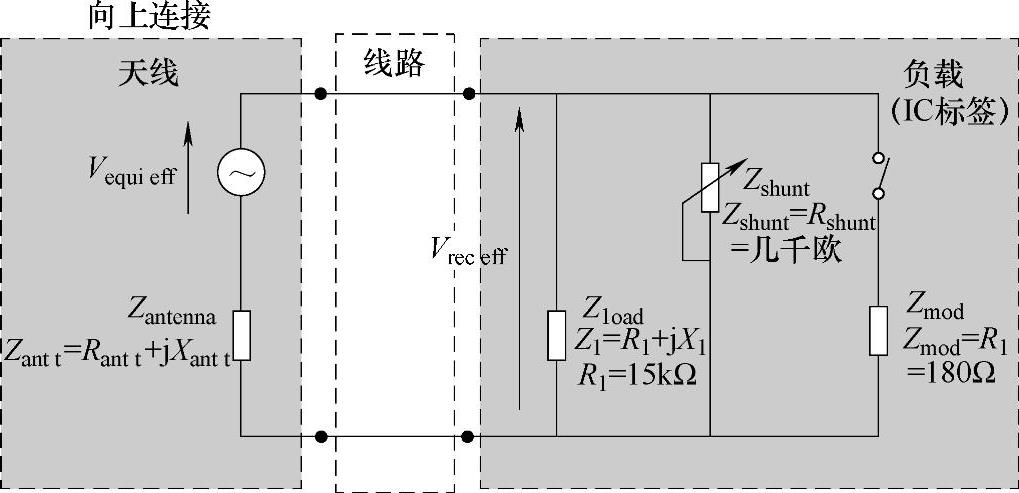
图3.10 标签在媒介区域——并联调节器开始正常进行

为此，将R_shunt的数值降低并且直接和天线的负载电阻并联，从而导致天线的结构不匹配，即使没有通过调制晶体管调制，α的标称值（未调制）也会减小为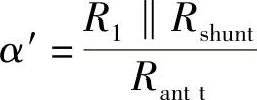。这是α=1，Γ₁=0的初始操作点（对应于操作阈值的点）的等效位移，转变为α′<1，且Γ₁不为0，为一个较小的负值（见图3.11）。

数据根据需要被传输到基站，标签的调制晶体管开始运转，使上面的值α′（此时它不再是合适的数值，所以不再会接收到最大功率，但是这不会影响标签，因为它更接近基站）转变为R_mod。因此，为了再辐射更多的入射波，可以调整后向散射面积（RCS）。

如图3.11所示，这种调整改变了α的值，也导致了ΔRCS更进一步的变化，使其比先前的变化值小。进一步而言，也就是当标签靠近基站的时候，ΔRCS的数值会减小。那么接着的问题就是：会产生低于标准所要求的最小ΔRCS吗？为了回答这个问题，必须考虑最坏情况。

5.标签位于非常靠近基站的位置

该标签被正确充能，甚至远高于其绝对的最低水平（见图3.12）。

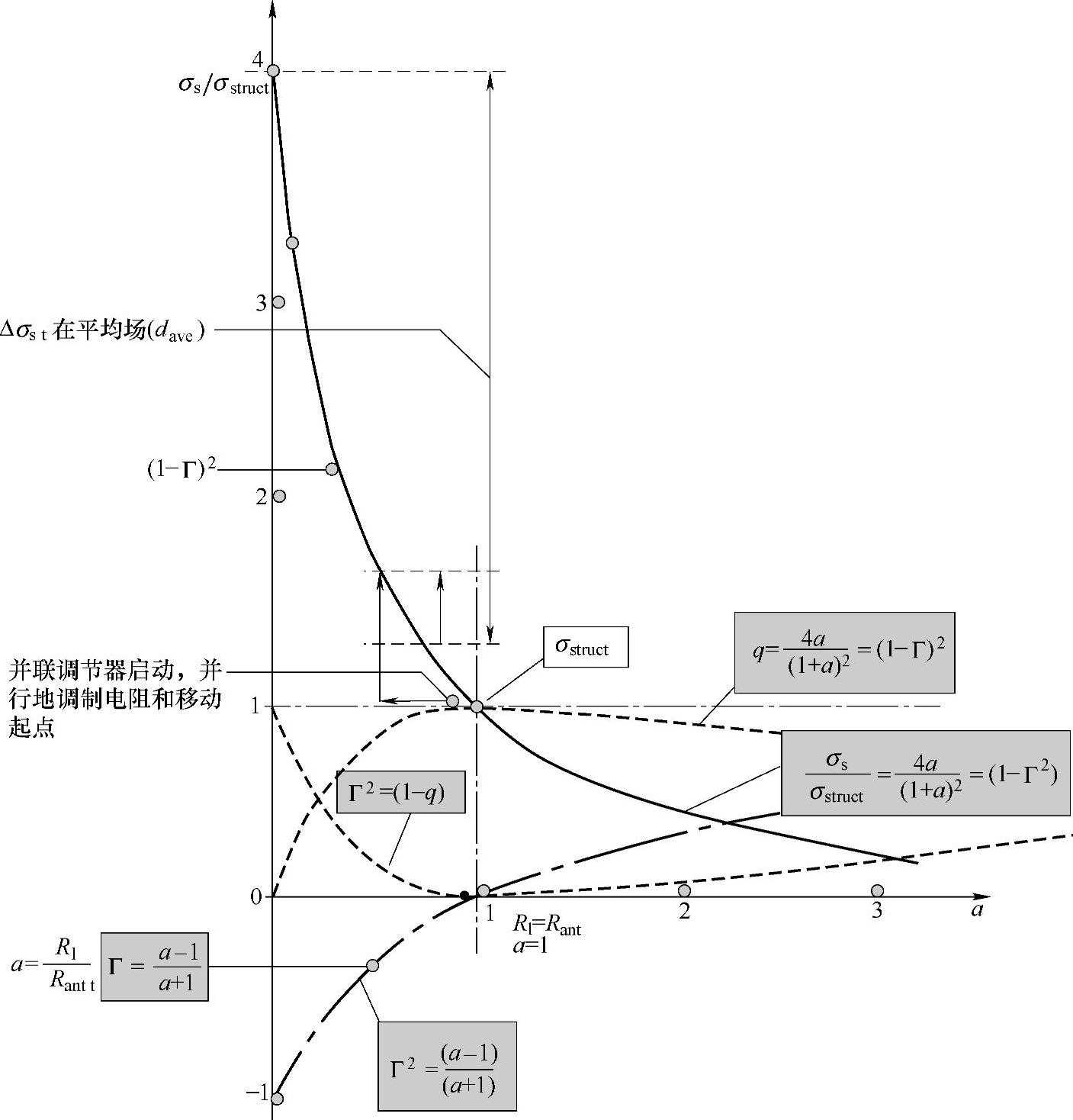
图3.11 以Γ₁的位置的变化作为磁场强度的函数

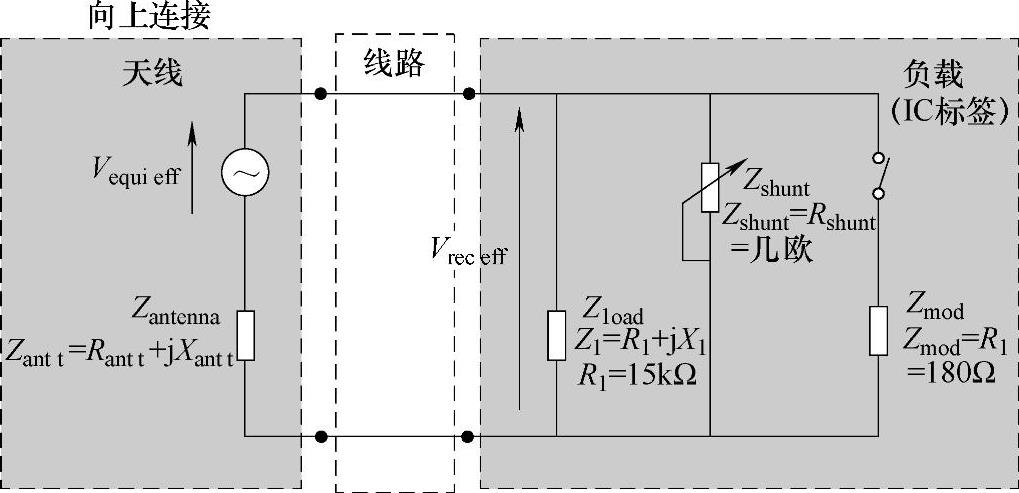
图3.12 标签在强场中-并联调节器是完全导通的

并联调节器是满负荷运转的，因此限制了集成电路输入端的电压。为此，R_shunt的值会变得很低（在几欧姆到几十欧姆），并且与天线的负载电阻直接并联，这样即使信号没有被解调器解调，也很容易导致天线结构失配。因此α的标称值（未调制）会很大程度的减小，变为α″=（R_l‖R_shunt）/R_antt。这等于将α=1的初始操作点（在操作阈内）转变成为α″，其中α″位于图3.13中非常接近垂直轴的位置，并且Γ₁的值接近-1。

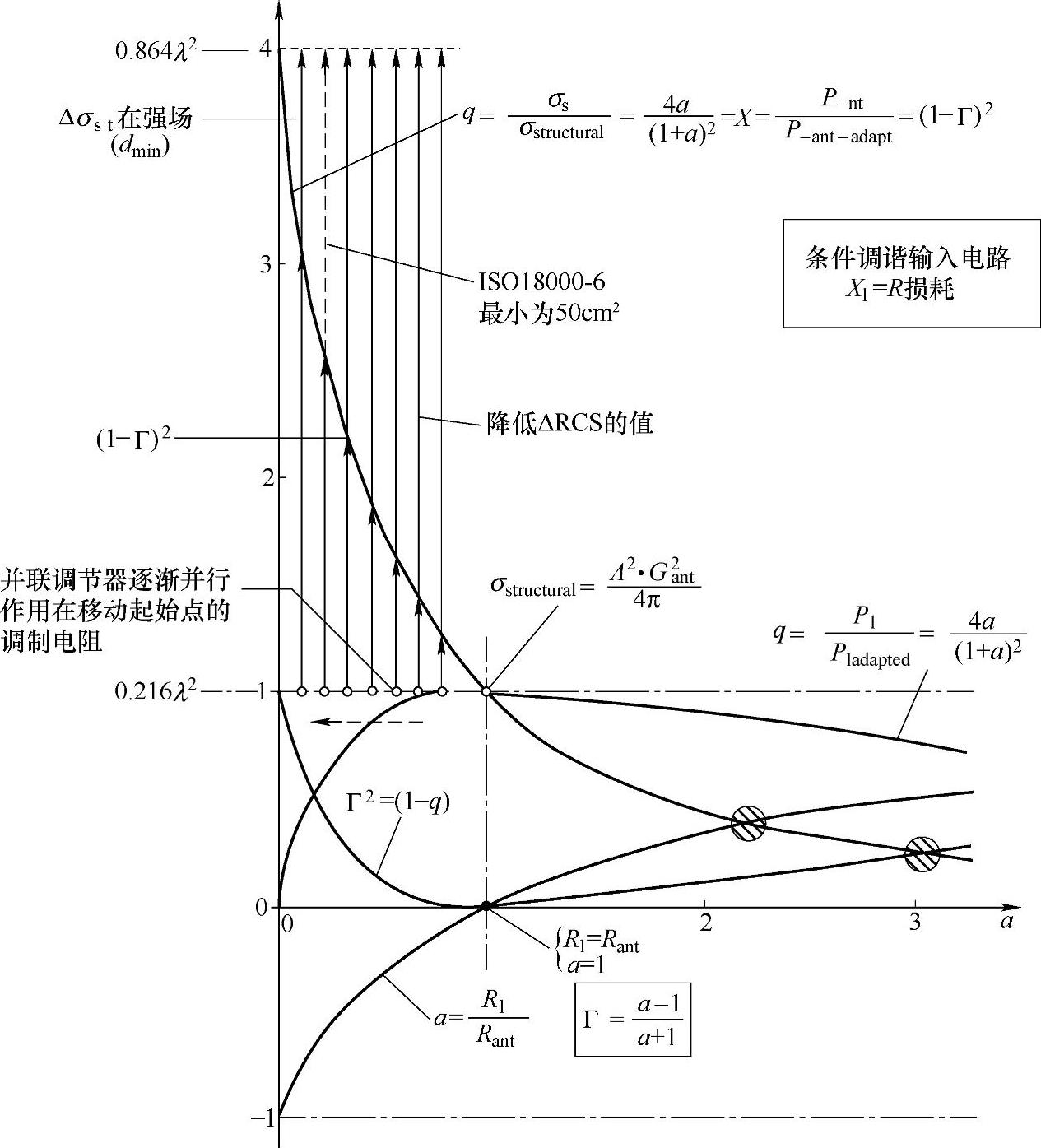
图3.13 在强场中Γ₁位置的限制情况

根据被传输到基站的数据，为了再辐射一些入射波，调制晶体管继续尝试操作，它通过切换α″的值（R_adapt∥R_shunt∥R_mod≈R_shunt∥R_mod）来尽可能地调整后向散射面积（RCS）。

如图3.12所示，这样的调制不仅改变了a和Γ的值，而且还引起了ΔRCS值的进一步变化，这比之前的变化更小。当α″非常接近垂直轴时，ΔRCS的值甚至更小，但肯定大于符合标准要求的最小值。这限制了R_shunt的最小范围和最小值，因此这也限制了标签能接收信号的最大强度区域E。此外，由于功耗的原因，芯片制造商在其集成电路上指明了最大输入电流，比如10mA或30mAeff（参见本书前2章）。

6.在强场中遵从ISO 18000-6标准的真实案例

正如所看到的，随着标签接近基站，并联调节器逐渐进入运行状态，Γ₁的值（在天线负载的相位没有调制）趋近于-1。

如果希望即使在信号很强的区域也能遵从ISO18000-6，那么Δσ_estypical的值必须等于50cm²。使用一个半波长的σ_estructural值大约是200cm²、并且频率在900MHz的双极子，同时在调制相位的时候使天线完全短路，这样在调制过程可以使得Γ₂=-1。在这种情况下，可以通过下面的式子来确定Γ₁的临界值：

Δσ_es2=σ_es2-σes₁

Δσ_es=ΔΓ[-2（Γ₂+Γ₁）]σ_estructural

Δσ_-=[-2（Γ₂-Γ₁）+（Γ₂-Γ₁）（Γ₂+Γ₁）]σ_estructural

传递值为

50=[-2（-1-Γ₁）+（-1-Γ₁）（-1+Γ₁）]×200

得到了一个关于Γ₁的二次方程式-Γ²₁+2Γ₁+2.75，解为

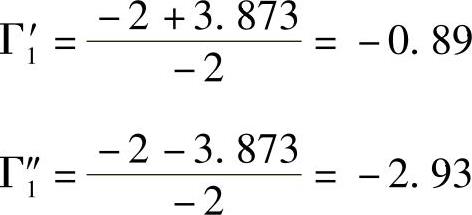
式中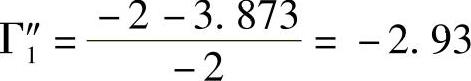，不符实际，因此舍去。所以Γ₁=-0.89（标签未被调制，在强场中，并联调节器满负荷运作）

如下式所示，可以确定α的值：

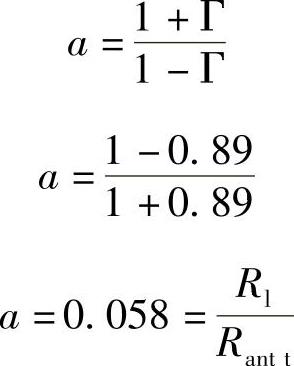
由此可见，为了不超出ISO 18000-6要求的最小值，分流电阻的最小值不应低于R_shuntmin=0.058×73=4.24Ω（与R_antt=73Ω相匹配）。该点位置已在上图3.13中标出。

7.通过总结得出以下结论

由上面的推导可知，随着接近基站Δσ_es的值会减小。精确测量数据显示，Δσ_es的测量值变化大体上与r²成比例。此外，通过标签的再辐射功率的变化值ΔP等于sΔσ_es。现在，入射功率通量密度s等于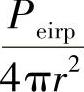，表明不管操作的距离，标签再辐射的ΔP实际上是固定的。这一特性的形成主要是由于并联调节器的存在和运行。

这部分总结了本章关注的主要理论，内容涉及反射、吸收和后向散射传输的原则以及它们之间的影响。不幸的是，你肯定已经意识到了，RCS和Δσ_es（或ΔRCS）的概念是比较难于把握的，并且其涉及的值也不是非常容易衡量。