让回到Δσ_es的通用公式，可以有如下发现：

Δσ_es=ΔΓ[ΔΓ+2（Γ₁-1）]σ_esstructural

首先，应该注意Δσ_es的值是两个相关联变量的函数，为了简单起见，我们将探索在什么情况下Δσ_es=f（ΔΓ）中Γ₁是个常量。

先观察一下。理论上，ΔΓ的最大值有限定范围，即（0，2]，因为变量Γ可以从-1变化到+1。实际上，因为有许多的无线射频识别应用是远程供电的，需要恢复一些入射能量去供给远程供电类型的标签，变量的变化范围就会减小（0～-1），见表3.1。

表3.1 变量变化

现在仔细看看在表3.1中前两列展示的两个常见的情况，这两种情况代表了大多数常见的无线射频识别应用。

（1）常见的远程供电应用，Γ₁=0且Γ₂=x。

大量的RFID应用是在远程供电的模式下运行的，因而从初始的未调制位置的共轭匹配开始，即是R_l=R_{annt_t}且a=1，也就是，Γ₁=0，然后转化为不同于在R_{annt_t}里的R_l，得到一个新值Γ₂。并且仅在这个情况下，ΔΓ=Γ₂，下面的等式可以化简为

Δσ_es=Γ₂[-2+Γ₂]σ_esstructural

Δσ_es=Γ₂[Γ₂+2]σ_esstructural

Δσ_es=[Γ²_mod-2Γ_mod]σ_esstructural

表3.2列出了Δσ_es值的例子

表3.2 Δσ_es值的例子

让我们看看当Γ₁=0时常出现的两种子情况。

1）子情况1：在UHF RFID中，为了最大化变量Δσ_es的变化范围，R_l常在共轭匹配的情况下从R_l=R_{ant_t}，a=1转化为R_l=0（负载短回路）。这样同时会出现两种情况，即a=0和Γ=-1，因此：

Δσ_es=σ_es-σ_esstructural=（4-1）σ_esstructural=3σ_esstructural

2）子情况2：在RFID中，有的时候会在RCS中的变量和标签功耗之间取折中值用以最大化系统的工作范围，因而R_l被设置为与匹配值R_{ant_t}之间存在小误差的值。仅仅在这个情况下，a=R_l/R_{ant_t}，即a的值接近或者等于1，并且Γ₂接近于0。此时，Γ²₂会小于-2Γ₂。所以，只在这个特别的情况下，Δσ_es=σ_{esantennamode}≅-2Γ₂σ_esstructural。此时曲线达到完美匹配（在a=1也就是Γ=0的点处曲线的斜率）。

（2）自主供电的常见情况，Γ₁=+1，Γ₂=-1。

因为该应用中使用的是带电池的标签，所以不需要为标签远程供电。这样我们的目标就是通过将开路改为短程回路来调整负载情况以便扩大Δσ_es范围。如果未调制时的Γ的初始值Γ₁等于1（也就是开路负荷），那么上述等式变为

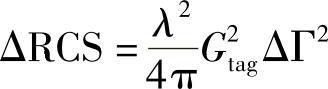
上式可以化简为

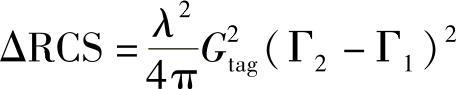
这个等式常出现在这个领域的许多图书和文档中，但是这些资料没有指出限制条件（只对于带电池的标签）。表3.3展示了Γ₁=1时的各值的情况。

表3.3 Γ₁=1时的各值

1.无线射频识别的一个例子（远程供电标签）

在一般或特定的条件中，为了调制标签中σ_es的范围，R_l的值被适当减小，或者用可变电容二极管来增大或减小调谐电容的值；但是通常情况下，不能同时改变这两个值，因为负载R_l=R_antt的电阻部分用到了（R_antt-dR）中的一个值并且它们中的电抗部分X₁=-X_antt用到了（-X_antt+dX）中的一个值。让我们返回到最原始的流过等效电路的电流I的等式为

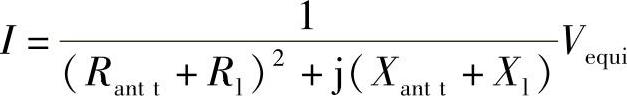
在分子和分母上乘上分母的共轭量为

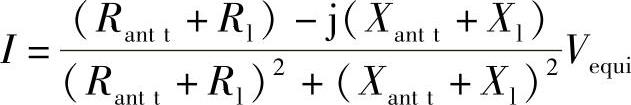
上式转化为

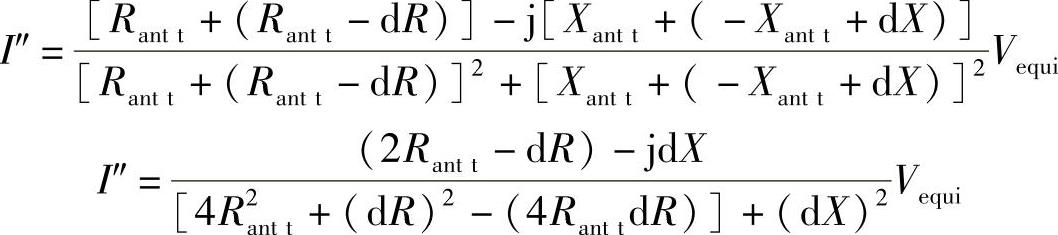
2.标签操作的假设情况

假定全部的负载电阻与匹配时存在微小误差，换句话说，dR比R_antt小一些，或者dX比X_antt小一些，那么式中（dR）²、（dX）²和（4R_anttdR）项相对其他项来说是可以忽略的。

这样，就得到：

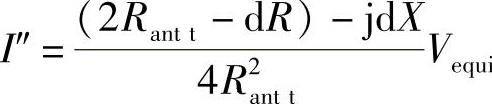
上式最终可以化简为

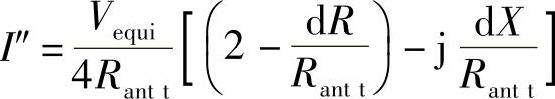
现在通过和前面相同的计算方法得到在阻抗调制阶段新的有效的RCS σ″_es。通过定义可知，标签P″_s的转发功率为

P″_s=（R_anttI″²）G_antt

因而得到了一个新的复数值I″为

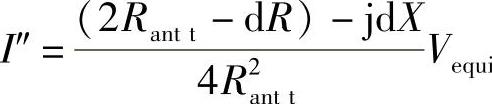
能计算出它的有效值（也就是说它的系数的值）为

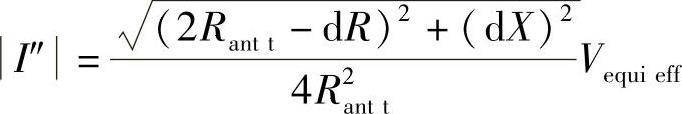
然后平方可得

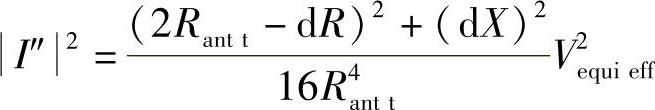
在本例中，再辐射功率P″_s为

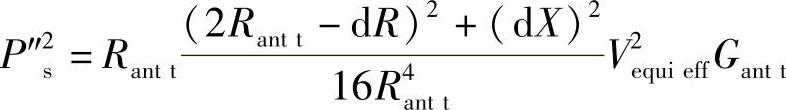
来自基站的标签所接收的总结构功率P_t为(www.daowen.com)

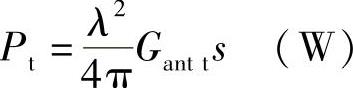
因此，

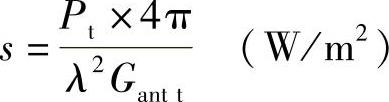
再辐射功率P″_s转化为

P″_s=σ″_ess

然后有，

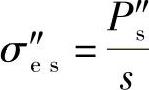
现在将s的值转化为σ_es等式，即

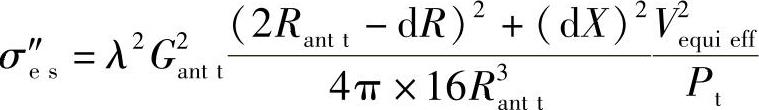
可以看出当天线的阻抗和负载相符时，功率P_t等于负载时消耗的功率，例如，

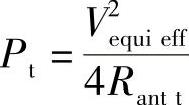
将这个值代入前面的等式中可以得到，

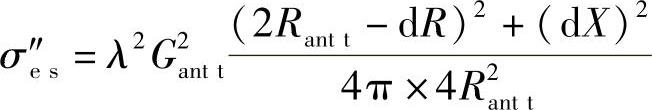
如果扩大分子，并设想dR很小，也就是说dR²和dX²可以忽略不计，这是因为相对这个等式它们是二阶无穷小，可得

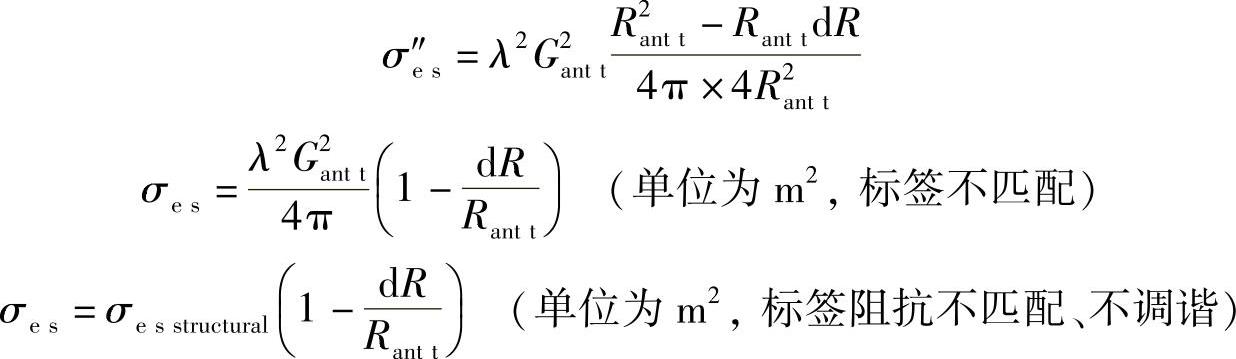
总结来说，通过给出的等式结果，可以认为（1-dR/R_antt）与（1-Г）²=（1-2Г+Г²）～（1-2Г）是一致的，因为此时dR<<R_antt，则Г²远小于Г。因此，

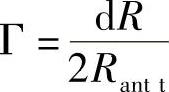
能得到这样的结果这是因为

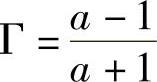
式中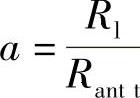，。如果R_l近似于R_antt（也就是dR很小），a近似于1：

1）若a近似于1，则分子（R_antt+dR）-R_antt=dR；

2）若a近似于1，则分母（R_antt+dR）+R_antt=2R_antt，这是因为dR很小，于是，

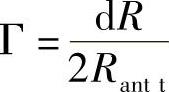
注意：

我可能花了很长时间推导了上述的方程式，在一系列严格的证明后仅得到了有用的近似结果，但这并没有结束。只用了这种方法，这是因为我们想提供给读者一个简单的方法以便他们在特殊的RFID应用环境下的计算。

还应当指出这些等式并不依赖于dX，因此，在这种情况下，RCS的变化根本上是由于dR的变化，并且这个值在很大范围是不会变化的。

注意：

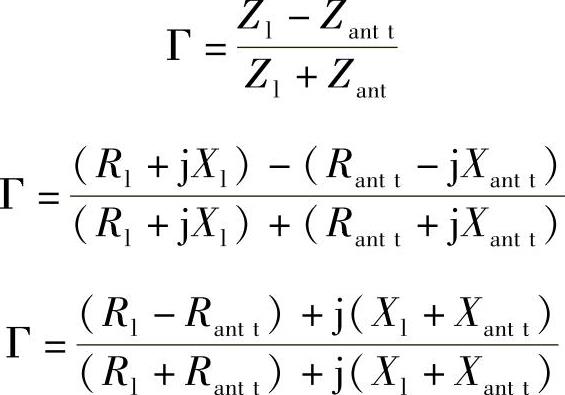
如果将这个表达式的分子和分母乘以分母的共轭，可以得到

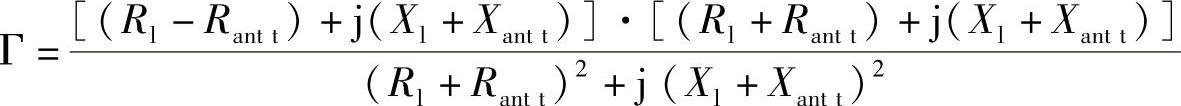
如果是最佳匹配（天线的输出阻抗和集成电路的输入阻抗是共轭的，例如：R_l=R_antt并且X_l=-X_antt），那么Г=0，最大的可用功率将转移给负载。在进行更深入的研究之前，让我们首先回顾UHF和SHF RFID的指定的应用。标签阻抗首先是匹配的，然后逐步失配；也就是说，负载R_l=R_antt的阻抗部分的取值为（R_antt-dR），电抗部分X_l=-X_antt将会取值（-X_antt+dX）。

在等式Г中用新的值替换R_l和X_l，可得

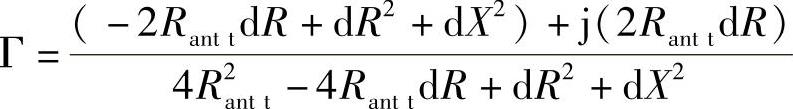
假设电阻dR和电抗dX的变化都很小（一个很小的解谐标签），在第一步的近似中，可以忽略dR²、dX²和dRdX，这些都是二阶无穷小。这样简化之后，可得

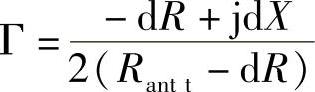
由于dR<<R_antt，

当其失配时，可得

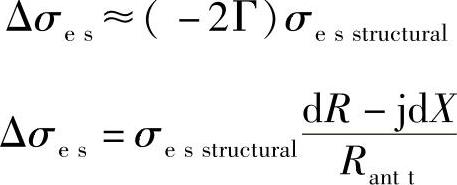
括号中的值是标签调制的品质因数，说明了包含在Δσ_es的值中的实部和虚部。

3.关于UHFRFID系统中使用后向散射相位调制的重要说明

值得注意的是，得出这样的结果是基于开始时所假设的前提条件，如果dR很小甚至为零，只要dX的值被明显调整（例如改动或者调整网络中集成电路的电容，或者保证从基站到标签的前向链路中Z_ant等于Z₁），那么Δσ_es的值就是纯虚数。实质上，这就意味着在转发和返回连接通信阶段中的再辐射的功率值没有变化，仅仅通过内部阻抗调制改变了标签再辐射产生的信号相位。在本例中，基站接收器必通过相位调制解调后向散射信号，而不是用之前用于接收功率的幅度变化调制（ASK）。一般而言，在99%的具有I、Q解调器的商用基站中，总是同时进行振幅和相位的调制。

4.匹配因子

为了总结这个例子，现在计算标签匹配因子的值，即

θ_matching=1-|Γ|²=q

先计算这个表达式的模，即

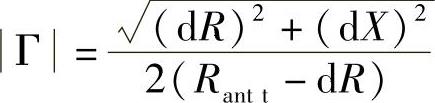
平方后得

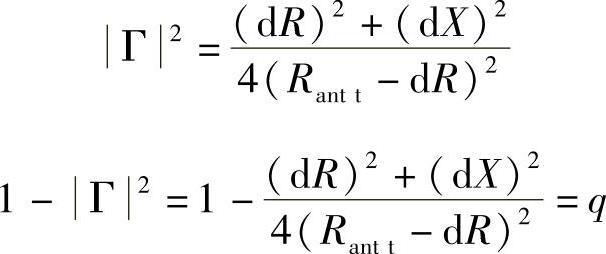
理论上，集成电路的输入阻抗R_l不等于73Ω。所以，通常通过一个阻抗匹配电路（变压器或者LC电路）来调整集成电路使其阻抗始终保持为73Ω（在2V时，35μW，P=U²/R_l→R_lic=80kΩ）。