在一个无线射频识别应用中，事先并不知道未调制的初始标签位置对应的物理形式（是完全匹配，近似匹配还是完全不匹配），或Γ₁=Γ_nonmodulated中相应的值。为了简化问题，未调制的物理状态应根据不同应用设计而采用不同的原理。例如，如果系统设计师确定标签应该为带电池的类型（有一个内置电池，但是仍然是被动通信类型的回程链路），因为应用需要在很大的范围内进行操作，因此标签天线在未调制位置不必预先匹配以恢复最大能量，因为标签中带有电池。

与现在所能阅读到的有关这个问题的相关资料不同，本节将通过没有任何预先假设的说明来考虑这种应用中所有可能的情形。

Γ₁=Γ_nonmodulated（未调制位置的初值）

Γ₂=Γ_modulated（负载阻抗被转化后的值，也就是在调制之后的位置）

ΔΓ=Γ₂-Γ₁=Γ_modulated-Γ_nonmodulated

使用通用方程，可以写出：

-σ_es=σ_esstructural+σ_{e s antennamode}=固定部分+可变部分（正的或是负的）作为负载R_l的函数

-σ_es=σ_esstructural+[{（1-Γ）²-1}σ_esstructural]

-σ_es=（1-Γ）2σ_esstructural

式中，σ_es=σ_esstructural+σ_{esantennamode}有一个固定部分和一个可变部分，已调制状态和未调制状态的差值被简化成两个等式中的可变部分σ_{esantennamode}之间代数差，即是σ_{esantennamode}和σ_{esantennamodenonmod}（见图3.5）。

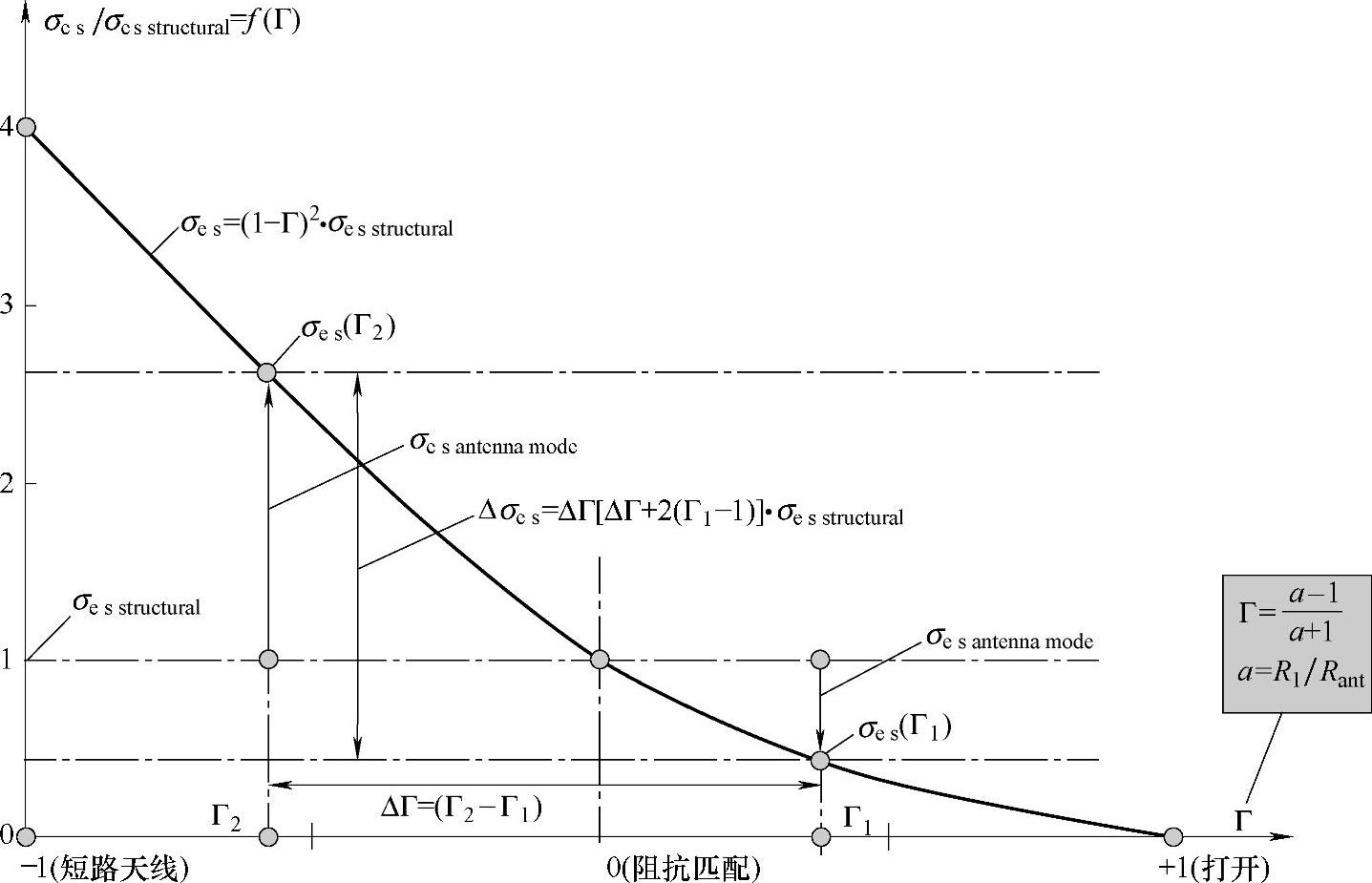
图3.5 计算和Δσ_es=ΔRCS的变化(www.daowen.com)

Δσ_es=标签的ΔRCS=σ_{esantennamode}-σ_{esantennamodenonmod}

现在来计算相应的σ_es1和σ_es2的值。得到：

1）在未调制阶段：σ_es1=σ_esstructural+[{（1-Γ）²-1}σ_esstructural]。

2）在调制之后的阶段：σ_es2=σ_esstructural+[{（1-Γ）²-1}σ_esstructural]。

约简后，影响因素就变成了：

1）Δσ_es=σ_es1-σ_es2。

2）Δσ_es=ΔΓ[-2+（Γ₁+Γ₂）]σ_esstructural

最后将Γ₂替换成（ΔΓ+Γ₁），得到：

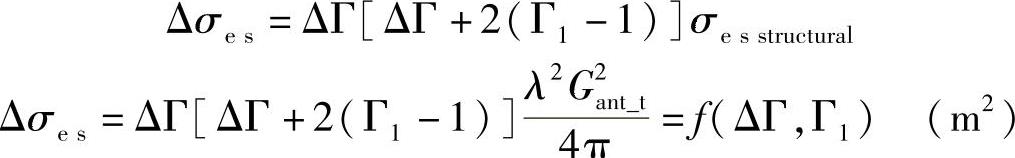
值得注意的是函数中的Δσ_es=ΔRCS同时依赖于两个元素：变量ΔΓ和代表初始值Γ₁的参数。