【摘要】:在第2.2.3节中,电路模型的实际意义为生产所需的带通效应,即可以用来计算最佳天线阻抗和匹配电路[DEA09]。通过调整经典的双调谐理论来拟合图2.33的模型,最佳双调谐匹配的首要条件是选择谐振频率相同的串联和并联的谐振电路:式中,ω0等于频带的几何平均数,即。α是剩余调谐参数。如果想改变α,还需要修改ωa——天线的谐振频率,使得该系列电路的谐振频率维持ω0。最优双调谐匹配提供了双调谐外的最大带宽[LOP 07]:
在第2.2.3节中,电路模型的实际意义为生产所需的带通效应,即可以用来计算最佳天线阻抗和匹配电路[DEA09]。假设给定的设计参数是:
(1)天线形状系数在很大程度上决定了Qa和Ra;
(2)集成电路的输入阻抗。
通过调整经典的双调谐理论来拟合图2.33的模型,最佳双调谐匹配的首要条件是选择谐振频率相同的串联和并联的谐振电路:
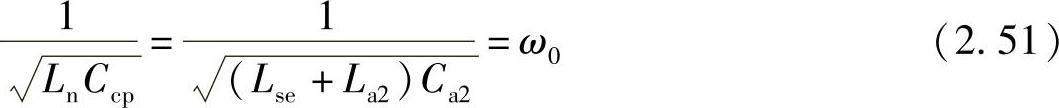
式中,ω0等于频带的几何平均数,即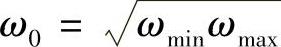 。由此可以看出,一旦ω0给出,Ln则可以由芯片电抗完全确定的。
。由此可以看出,一旦ω0给出,Ln则可以由芯片电抗完全确定的。
α是剩余调谐参数。α的任何改变将改变Lse,因此也会改变串联谐振。如果想改变α,还需要修改ωa——天线的谐振频率,使得该系列电路的谐振频率维持ω0。通过结合式(2.42)和式(2.51),可以得到ωa的二次方程式:

这是通常的解决方式。通过使用式(2.43)在La方面,式(2.52)可以被改写:
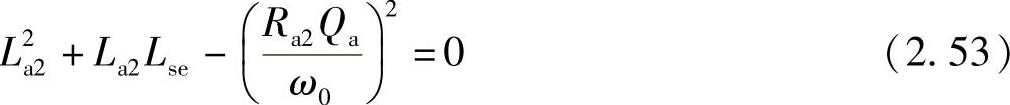
最后,通过应用二次方程和正向电感,可以求得总的天线电感:
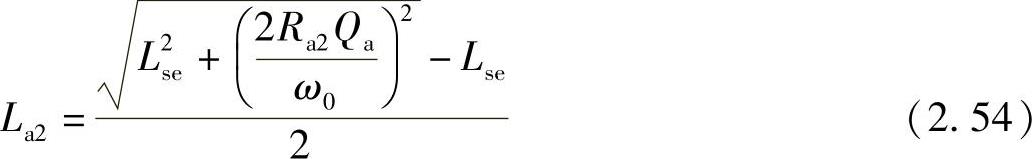 (https://www.daowen.com)
(https://www.daowen.com)
或相当于:
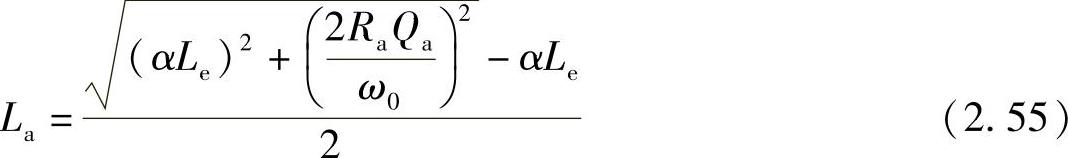
最后,电感是由金属的扁平或带状线(矩形截面)构成,使用下列估算:

式中,w和l分别为宽度和跟踪长度;t是金属厚度(单位为cm)。一旦先前的值固定,有可能在ω=ω0时确定反射系数,串联和并联谐振电路谐振:
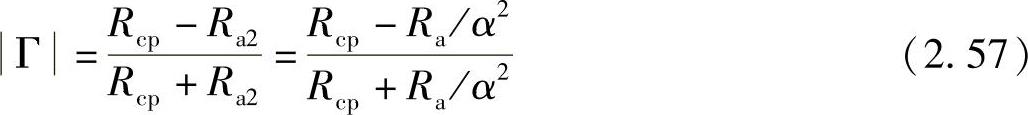
或在PTC方面:

在式(2.57)和式(2.58),|Γ|和τ是最严重的反射系数和最坏的PTC,分别允许通过带宽以及在ω=ω0观察。
最优双调谐匹配提供了双调谐外的最大带宽[LOP 07]:
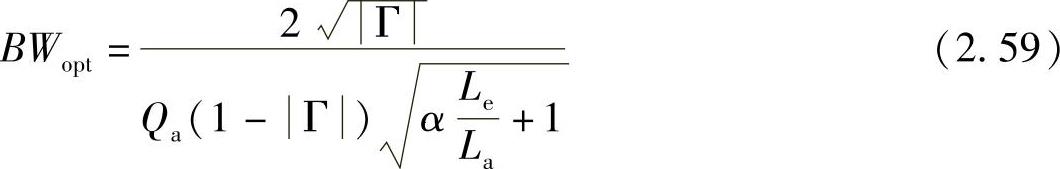
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章





