1.等效电路

偶极子组成大部分天线设计最基础的部分，它可以用金属线或者金属条构成。如图2.1所示的偶极子，当给输入端加上电压时，输出端就会产生负电荷。从本质上来说，偶极子末端可以看成开路，只有高电压但没有电流，但由于电荷聚集在偶极子的两端，从而可以通过电流。因此，任何天线都能立刻充电并产生电流。在电路模型中，这些通电装置都会分别连接一个电容和一个电感。如果正负极电源距离等于一个波长的长度，则在空间内从偶极子的不同部分到一个点的阻滞能够防止辐射衰弱，并且能够加强某个方向的效果。能量流入空气中的过程能用一个阻值模拟。

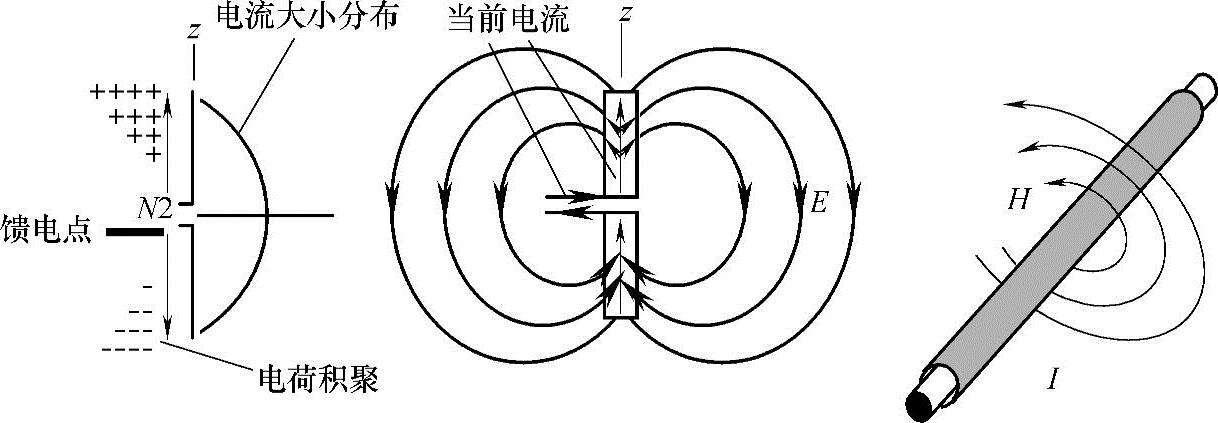
图2.1 偶极子天线电压和电流的分布

忽略天线厚度的影响，超高频带半波偶极子天线的长度在915MHz时大约为16.4cm，在谐振附近的相对窄的带宽内，一系列RLC电路能够很好地预测半波偶极子的谐振效应，而电抗则和串联LC电路相关，但电阻实际上并不恒定，这样一个谐振频率电路如图2.2所示。

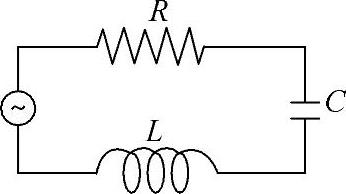
图2.2 半波长偶极子天线的等效RLC电路

基本的半波偶极子不能很好地解决UHF RFID的问题，有两个原因：首先，是因为对于UHF标签来说它的长度太长；其次，谐振时的天线电抗太小，而电阻太大，不能有效匹配典型的低阻值、高电容值的UHFRFID的集成电路。

在RFID工业应用中，考虑到标签范围在102.6mm内的便利性，天线长度通常接近92mm。但是一个短于半波长的直偶极子具有负电抗，所以引入一个额外的电感线圈使得短天线在频率低于固有频率下谐振。用下式表示长度为l和直径b的偶极子的电容C和电感L的关系[MCD 12]。

这些等式可用于当l<<c/f₀=λ₀，例如，对于l=3.33cm的情况，在900MHz时l=λ₀/10<<λ₀，会发现C=0.26pF，L=11.6nh，b=1mm。很明显可以看到短的线性天线的电抗是由于电容产生的，把电感L和电容C的估值代入式（2.1），得到l=λ₀/2.22，这对谐振提供了一个很好的预测同时为半波偶极子构造了物理模型。

2.辐射电阻、输入阻抗、效率和增益

辐射电阻R_rad被定义为一个等效电阻，其消耗的功率等于天线的辐射功率，此时天线中的电流为最大值。另一方面，任意天线的输入阻抗Z_a是根据终端电压和电流的比值来定义的。对于一个中心馈电偶极子，最大电流只有在λ₀大于1时（见图2.3）才等于终端电流。在这种条件下，对于一个无损偶极子，可以得出输入电阻等于辐射电阻（R_a=Re（Z_a）=R_rad）。

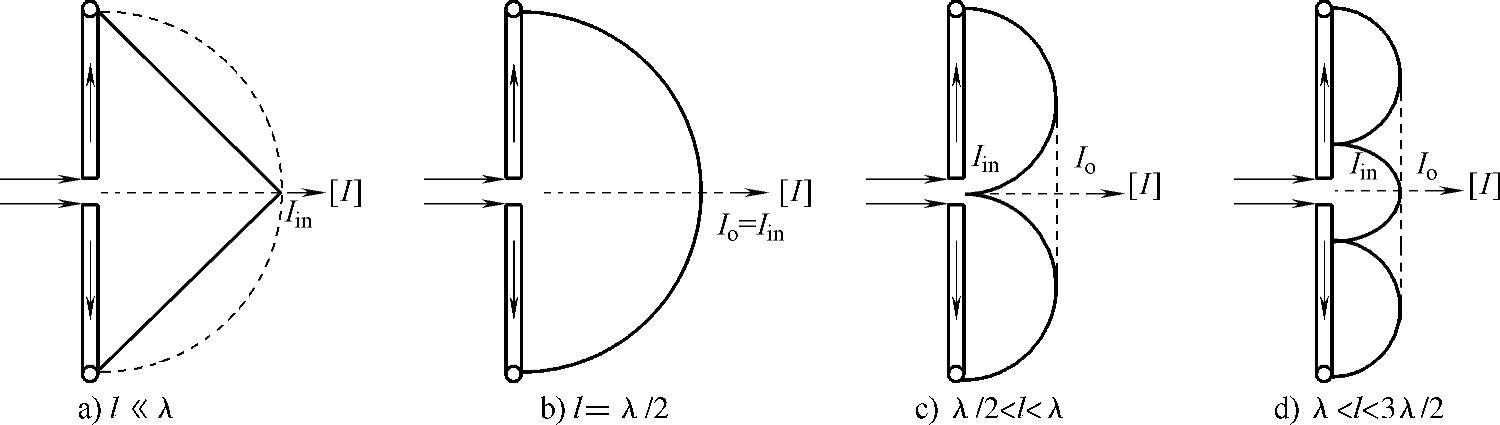
图2.3 不同长度的偶极子天线的电流分布

非对称偏馈的偶极子的输入阻抗Z_as和等长度的对称中心馈电偶极子的输入阻抗Z_s相关，输入阻抗Z_as与Z_s分别与它们在偶极子终端的电流I_as和I_s有关（见图2.4），利用以上条件，对于一个给定的电流，发射机输出功率必须等于天线的辐射（有功）功率和存储（无功）功率的总和，导出：

Z_sI²_s=Z_asI²_as （2.4）

非对称偶极子的偏馈分布在距离偶极子中心h处，假设电流呈正弦分布，式（2.4）变成：

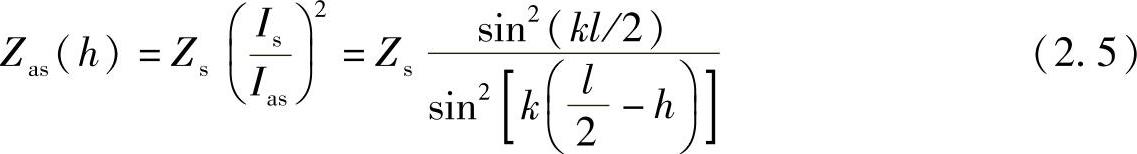
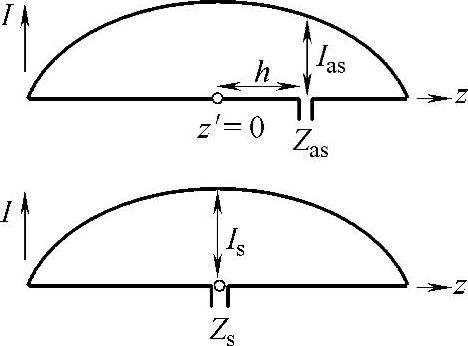
图2.4 对称偶极子反馈和非对称偶极子反馈的相关性

对一个半波偶极子，可进一步推导出如下表达式：

可以得出以下结论，通过抵消天线向电流为0的偶极子的末端的输入，输入电阻和电抗均增加。值得注意的是在各个部分的辐射阻抗是相等的，在中心馈电情况下，输入阻抗的实部等于辐射阻抗。

对于一个有损耗的天线，输入电阻R_a能被分解成两个不同的电阻：

R_a=R_rad+R_loss （2.7）

式中，R_rad表示辐射电阻；损耗电阻R_loss代表的是由于性能不是很好的导体和介质材料引起的额外损耗，线状或条状偶极子的辐射电阻在很大程度上取决于电流的分布。对于理想偶极子（λ>>1），电流是不变的，辐射电阻等于[BAL 05]

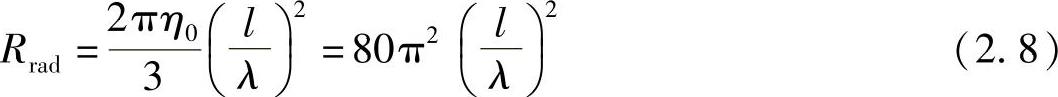
可以得出对于一个短的偶极子（λ/50<l≤λ/10），电流呈三角分布，最大值在中间，最小值在两边，式（2.8）的1/4近似值为

对于一个长的偶极子，电流呈正弦分布，中心馈电偶极子的辐射电阻十分接近于：

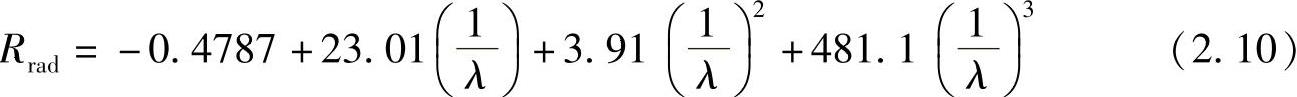
该式针对频率范围为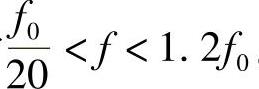。因此，式（2.10）可用于半波长度的偶极子，上限是l=0.6λ₀。

需要注意的是先前的R_rad的表达式不受天线的直径影响，只要1/b足够大就行。所以当偶极子较厚时，辐射电阻会稍有减少。在900MHz时，b/λ=0.003对应于b=1mm，辐射电阻近似等于62Ω；然而理想情况下b趋近于0，辐射电阻是73Ω。虽然电线的半径对电阻的影响不大，但反馈端的空间距离对电阻的影响却很大，尤其是在反馈点或反馈点附近的电流很小。

最后，由于传输损耗的电阻可用下式计算：(www.daowen.com)

天线效率_η定义为如下比值：

式（2.12）是辐射功率和天线输入功率的比值，假设工作频率在900MHz（λ₀=33cm），b=1mm，σ=5.7×10⁷S/m（copper），无损条件下的偶极子可以这样描述：

-R_rad=7.9Ω，R_loss=26mΩ η=99.7% 当l=3.33cm（l=λ₀/10）

-R_rad=712mΩ，R_loss=7.8mΩ η=98.9% 当l=1cm（l=λ₀/33）

为了更好地控制天线电阻，我们在[RAO05]里加入一个和曲线跟踪相同宽度的负载条。作为并联电容，它可以使一部分辐射阻抗分散到IC的输入阻抗中（见图2.5）。

天线增益用于描述有多少功率被从辐射峰值方向传输到同性电源方向，假定天线是由没有电阻的传导性材料构成，介电损耗为零，称G_lossless为理想无损天线的增益。由有损材料构成的天线的最大增益如下所示：

G=ηG_lossless （2.13）

式中，η是有损天线的效率，由于天线增益同时影响传输到芯片的功率效率和返回阅读器的部分入射功率，考虑到尺寸，天线增益，最大化一般低点是很重要的。

3.电压驻波比带宽和品质因数

天线的带宽（BW）能从它的基本特性，如返回损耗、输入阻抗、极化、辐射效率等方面定义。为了将天线带宽与Q值关联起来，使用匹配电压驻波比（VSWR）带宽会更便利，其可写作BW_VSWR。对于调谐天线，换言之在频率ω₀时的电抗为0，BW_VSWR在驻波比等于常数时是两边频率之差Δω，部分匹配的电压驻波比带宽由式（2.14）定义：

图2.5 曲线偶极子辐射电阻削减

这个定义只是在馈线的特性阻抗满足Z_a（ω₀）=R_a（ω₀）时有效。半功率的VSWR带宽对应S=5.828。反射系数平方的相关值为α=（S-1）2/（S+1）2=1/2，这意味着有一半的入射功率反射回来。

文中谐振器的品质因数是2π倍的存储在谐振器的能量（存储在电感和电容无损耗能量之和）除以每个周期在谐振频率下消耗在电阻上的能量：

品质因数的概念经常将天线描述为谐振腔。通常，在电路设计中，可以让电路中的组件有较高的Q值来减少线路损耗。但当谈论到天线时，我们想要一个低的Q值，因为其中的“损耗”是我们真正想得到的辐射。一个低Q值的天线对应着较高的带宽：

反之，高Q值的天线的特点是高谐振和窄带宽，因为它可以存储大量的能量，并且辐射相对较少。

考虑到小型天线时，品质因数的概念十分有用。小型天线的品质因数会由于低辐射和高电抗变得很低。天线越小，品质因数就会越大。如果用适当的方法降低指定的天线体积，品质因数就会提高[BES05]。品质因数和FBW_VSWR的关系如下[YAG 05]：

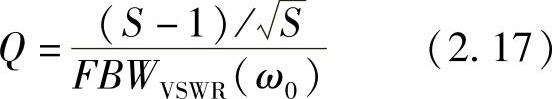
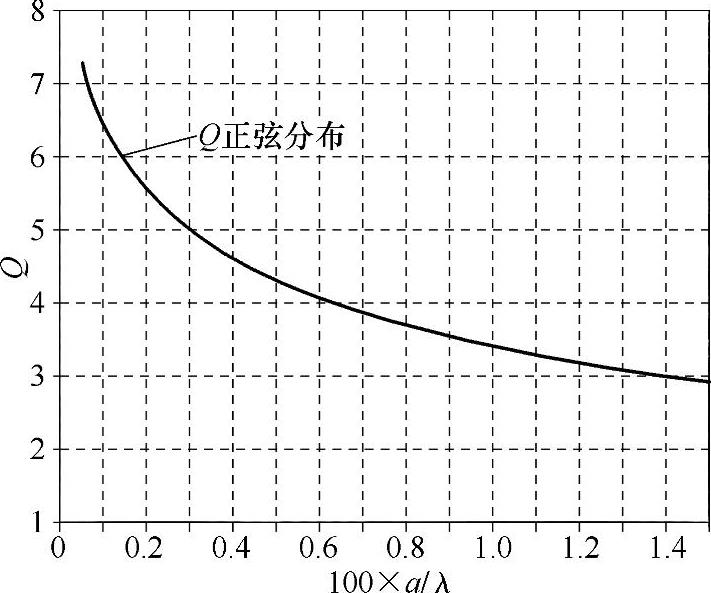
图2.6 Q值与偶极子辐射a=b/2的关系曲线[HAZ 11]

图2.6反映了品质因数是对半波偶极子波长归一化的线半径a=b/2的函数。可以看到半径为1.65mm时，Q值大约等于4.4，换句话说100×a/λ=0.5。然而，根据[STU 12]中的图6.7，FBW_VSWR在S=2、100×a/λ=0.5时是16%。将这两个值带入式（2.17），计算得到Q=4.41，这和图2.6中100×a/λ=0.5时的数值很接近。

全球范围内的UHF RFID标签的频率范围都定义在860～960MHz之间，此时的相对带宽为11%。因此，得出的结论是用连续的半波偶极子覆盖11%的UHF RFID是没有问题的。但是在后面中描述到的缩减技术将品质因数提高到了15，该技术将品质因数的提升作为主要问题。显然，如果标签对应一个单频带宽，那么在品质因数上的工作就会大幅缩减，而这项技术目前只在美国使用。

窄带天线的另外一个缺点就是它们的匹配很难，并且比宽带天线更容易去谐。

从图2.6中也很容易看出Q随着（a/λ）对数递减。结果就是，Q由6降到3时，需要线半径增加15倍（由0.6mm到10mm）。所以，长度与直径比值的大幅变化导致了Q值的提升较慢。

[MCL 96]描述了对于小型天线的最小Q值的基本理论限制。如果天线可以放置在以r为半径的圆的边缘，那么无损天线的最小Q值就是：

式中，k=2π/λ。这个式子给出了天线可以匹配的最小Q值。遗憾的是，这个理论没有告诉我们怎么样去实现这样的最小Q值。但是关键的一点是，拥有有效体积的天线可以缩小总的反应范围从而得到一个较低的Q值。[BES05]已经指出在球面螺旋几何中由多个折叠臂构成的天线占据了完整的球形体积，达到自身谐振和阻抗匹配。其最优的结果是理论最低Q值的1.5倍，此时电偶极子的效率达到98%。

但是RFID天线是平面的，并且一个电偶极子只是填充了边界区域的一小部分范围。结果就是在辐射r=λ/2区域内时用式（2.18）求出的约等于1的最优Q值比图2.6中曲线对应的Q值小。

到目前为止，我们只是考虑了线形偶极子。如果w=2b，那么宽度为w的平面偶极子的带宽约等于直径为b的线形偶极子的带宽[DEA10]。