事实上，式（1.3）只是对电压的粗略近似求解，因为该式中阈值电压被看作是常量。实际上，肖特基二极管阈值电压是由直流电流I_d和饱和电流I_S通过电流与电压之间的指数定律决定的（对于连接二极管的MOS来说，是通过平方律决定的）。因此，可以得到一个与二极管电流，即实际中的负载电流呈对数关系的二极管前向电压降，即

式中，η是二极管的非理想因子。因此考虑从属关系和通过饱和电流的工艺选择，式（1.5）可以写成以下形式，

在UHF RFID应用程序中，输入电压的振幅相当微弱，并且二极管在一个电压降严格依赖于电流的区域工作，如图1.4所示。

如图所示，当I_S是200nA时，通过二极管的电流在2～4μA变化。因此，电压降在60～75mV之间变化。

正如图1.5中对于一个1.2pF的耦合电容、一个12pF的输出电容和一个120nA的二极管饱和电流所进行的仿真[BAR 09]所示，由于非线性关系二极管电流具有脉冲波形。

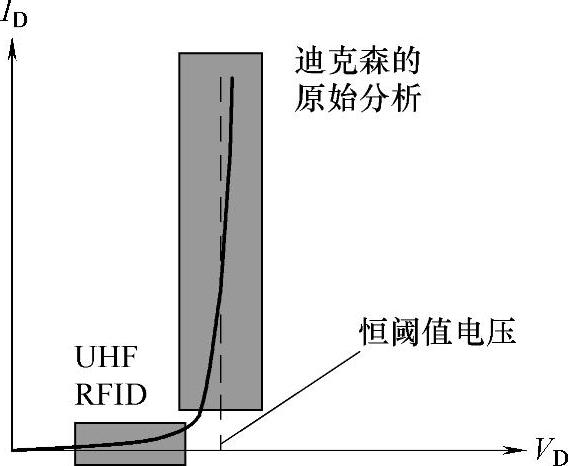
图1.4 在迪克森的原始分析和UHF RFID应用程序中二极管的工作区域

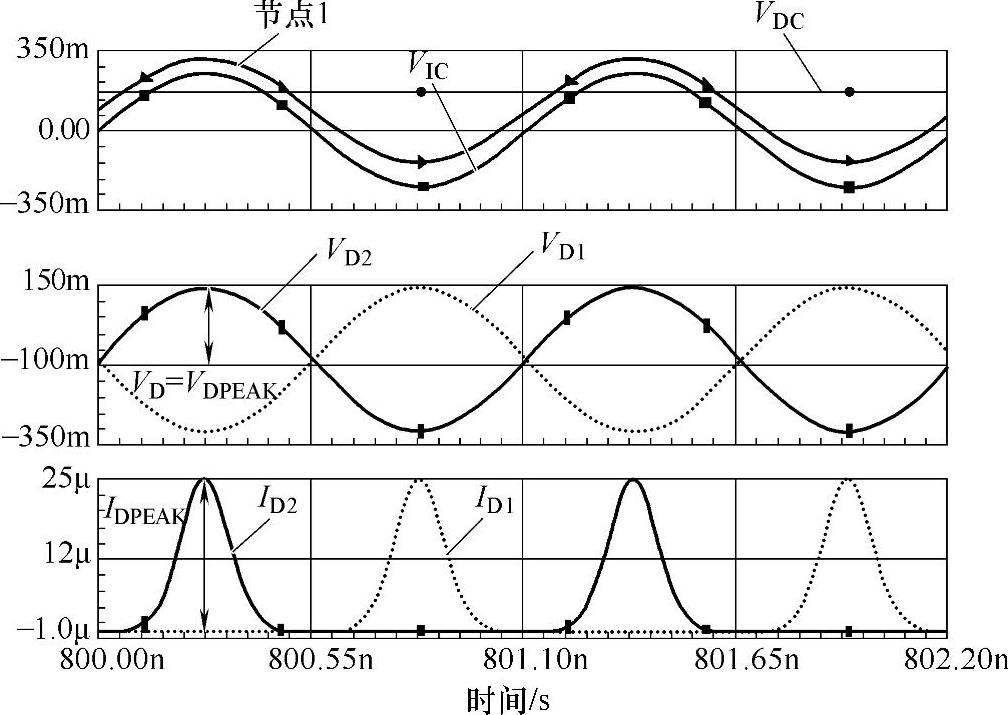
图1.5 在稳定状态条件下，在肖特基二极管双倍压器中的电压与电流(www.daowen.com)

正如所看到的，阈值电压不能被忽略，因为它代表了近似100mV的下降（依赖于DC），这个下降的数值与输入电压的振幅在一个数量级上。找到阈值电压的准确值很重要，因为一个很小的误差在经过几个级数后就会被放大，这样就会严重改变直流输出。

整流器的输出可以被视作电流源，它的值由IC的电流损耗决定。也就是说，由于电荷守恒，在一次传导循环过程中瞬时电流的平均值与来自输出的负载电流相等，在这个例子中I_out等于3.44μA[BAR 09]。因此，如果输出（或者负载）电流增加，峰值电流也会增加，从而导致在式（1.7）中的平均电流增加，即

类似的，如果输入电压增加，二极管电流的峰值也会增加，并且这样会导致脉冲形状的改变。

因此，从直流输出产生的观点来看，输入电压和输出电流决定了二极管的电压降。事实上，由于整流器的工作方式，阈值电压仅仅只由电流I^_d的峰值决定。因此，直流输出电压最终形式如下，即

在由余弦函数的指数形式的修正贝塞尔函数描述的电流和电压关系的基础上，一些作者（像De Vita和Iannaccone[DEV 05]）建立了对于一般N级整流器的输入输出关系：

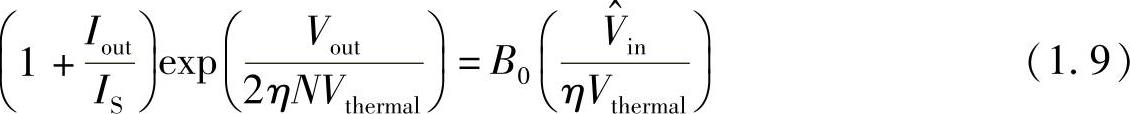
在这里，可以清楚地知道设计者选择V_out作为目标输出参数，而I_out为因变量[TEH 09]。