9.4.1节中对Hash表介绍的同时，也介绍了Hash表的建立方法，即根据给定的关键字依照函数H来计算关键字key在表中的地址，并把key存在这个地址上。下面用一个例子来体会Hash表的构造方法。

【例9-5】 关键字序列为{7，4，1，14，100，30，5，9，20，134}，设Hash函数为H（key）=keyMod13，试给出表长为13的Hash表。

求解过程见表9-4。

表9-4 求解过程

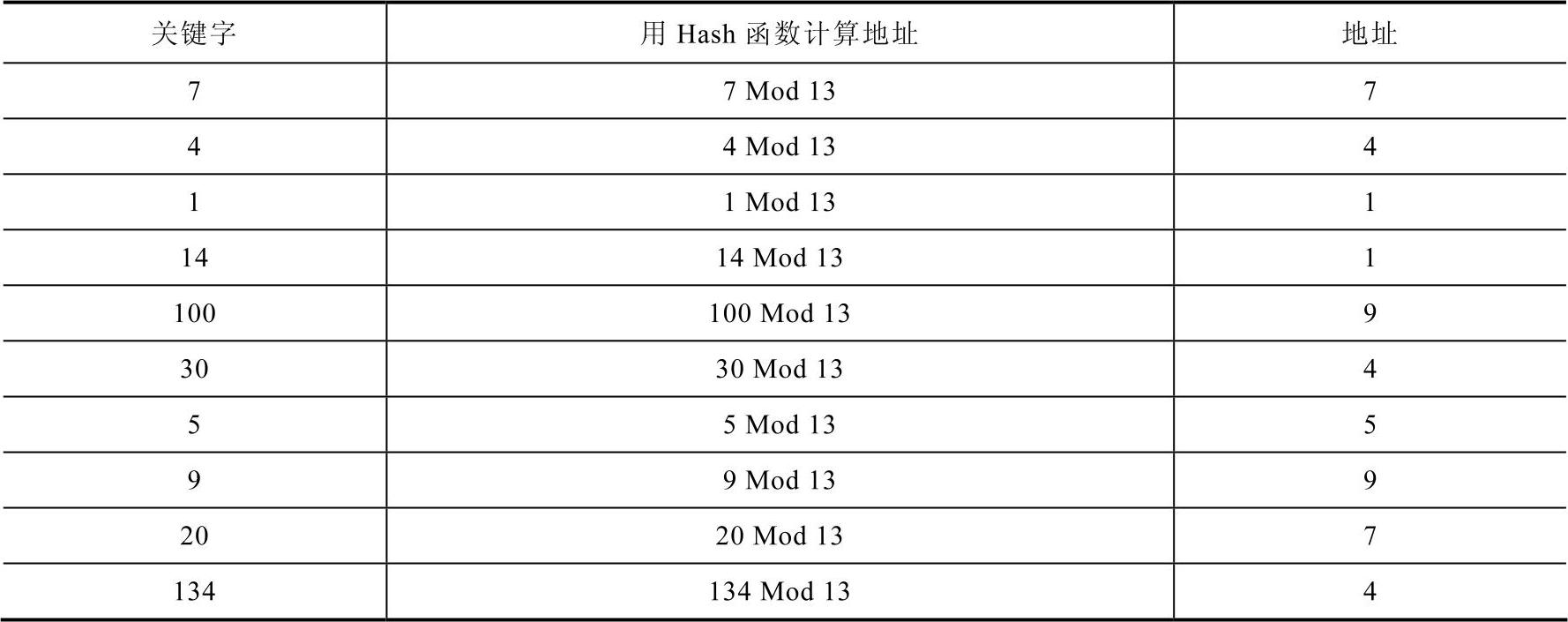
根据表9-4中所求各个关键字的地址，将关键字填入Hash表中，表9-5即为所得表。

表9-5 Hash表中有冲突

由表9-5可以进行关键字的查找了。例如，要查找关键字5，则只需将5代入Hash函数，由H（5）=5可知关键字在Hash表中的地址为5。但是从表9-5中还可以发现，有多个关键字共用一个地址，如地址4上就有4、30、134这3个关键字，这种情况称为冲突（当key1≠key2，而H（key1）=H（key2）时，称发生了冲突，这时也称key1和key2是Hash函数H的同义词），是不允许出现的。因此要做一些处理来解决冲突，使得每个地址对应一个关键字。

解决冲突的一种可行的方法为从冲突发生的地址d开始，依次探测d的下一个地址（当到达下标为m-1的Hash表表尾时，下一个探查的地址是表首地址0），直到找到一个空闲单元为止，将关键字保存在这个位置上。一般冲突处理的过程是穿插在建表过程中的，即边建表边检测冲突，当发生冲突时立即解决冲突。本例中包含解决冲突的建表过程见表9-6。

表9-6 包含解决冲突的建表过程

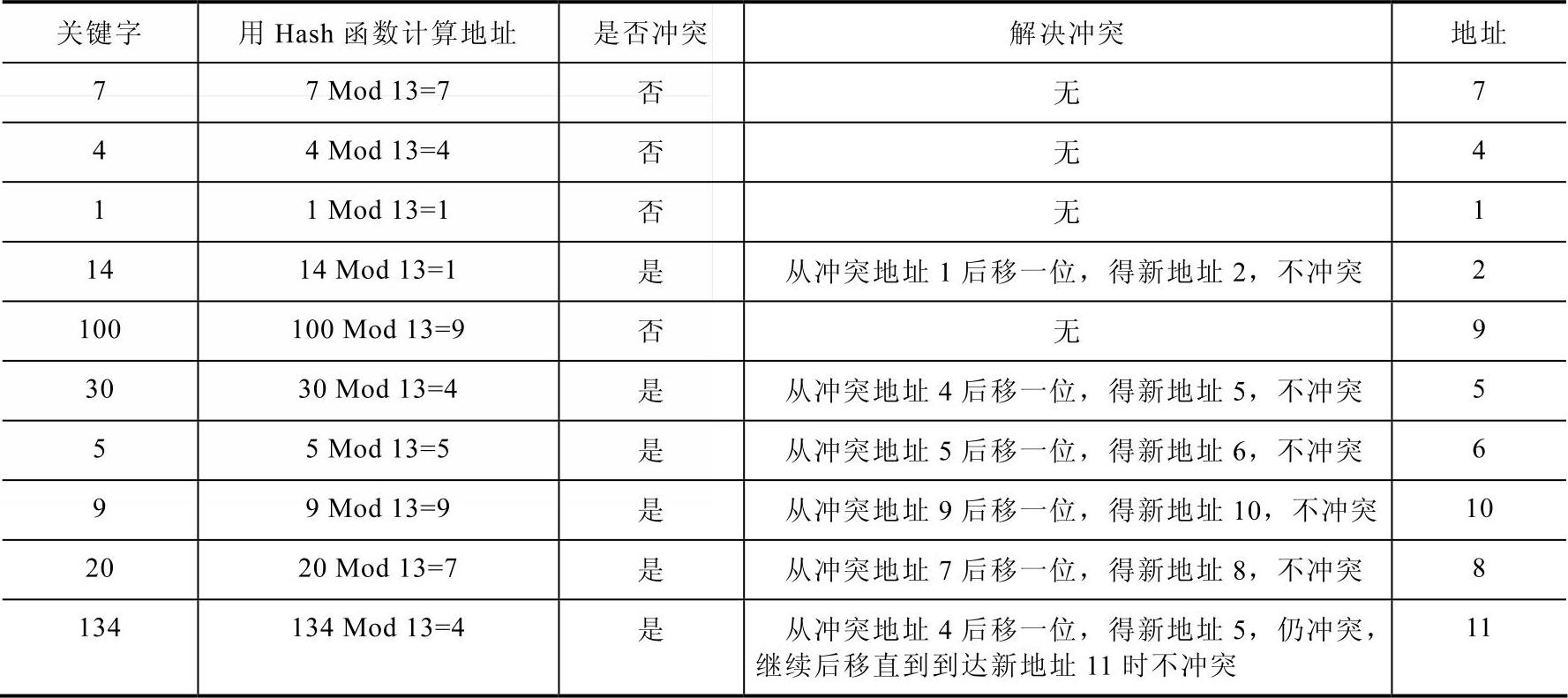
由此得到新的Hash表，见表9-7。

表9-7 Hash表中消除了冲突

Hash函数：H（key）=keyMod13

冲突解决方法：在发生冲突的时候，对i属于1～m-1，从冲突地址d开始依次进行H_i（key）=（H（key）+i）Modm运算，直到没有冲突为止，算出此时的地址为H_i（key）。

说明：H（key）是key的Hash地址，H_i（key）是对key解决冲突后的地址，注意区分。

加入了冲突处理的Hash表在进行查找时，不能只根据Hash函数来计算地址，还要结合冲突解决方法。

上述Hash表的关键字key的查找过程：先用Hash函数计算出一个地址，然后用key和这个地址上的关键字进行比较，如果当前地址上为空，则证明查找失败；如果和当前地址上的关键字相同，则证明查找成功；如果不相同，则根据冲突处理方法到下一个地址继续比较，直到相同为止，证明查找成功；如果按照冲突处理方法寻找新地址的过程中又遇到空位置，则同样证明查找失败。

例如，查找关键字30，由Hash函数得到一个地址4，经过比较发现和地址4上的关键字不同，则根据冲突处理办法后移，发现与地址5上的关键字相同，证明查找成功。查找关键字21，由Hash函数得到一个地址8，经过比较发现和地址8上的关键字不同，则根据冲突处理方法后移，一直移到地址12，发现为空位置，证明查找不成功。

讲到这里就可以给这个题目再附加一步，求在等概率的情况下查找成功和不成功时的平均查找长度ASL₁和ASL₂。

1）要求ASL₁，关键是求出对于查找每个关键字所对应的比较次数。通过上面的分析可以知道，如果没有冲突，则只需比较一次；如果发生冲突，则根据其冲突解决方法来计算出比较次数。例如，查找关键字30，由Hash函数得到一个地址4，经过比较发现和地址4上的关键字不同，则根据冲突处理办法后移一位，经过比较发现与地址5上的关键字相同，则查找关键字30的比较次数为2。可以对每个关键字求出其比较次数，见表9-8。

表9-8 关键字比较次数

根据表9-8可知：

ASL₁=（1+2+1+2+2+1+2+1+2+8）/10=11/5

2）要求ASL₂，关键是求出查找不成功情况下的比较次数。这里的比较次数是针对于表中每个可以通过Hash函数计算得到的地址来说的，对每个地址求出由这个地址开始的比较次数，然后求其平均数就是查找不成功时的平均查找长度。例如，查找关键字21，由Hash函数得到一个地址8，经过比较发现和地址8上的关键字不同，则根据冲突处理方法后移，一直移到地址12，发现为空位置，证明查找不成功，比较次数为5，即对于地址8，其对应的查找不成功的比较次数为5。

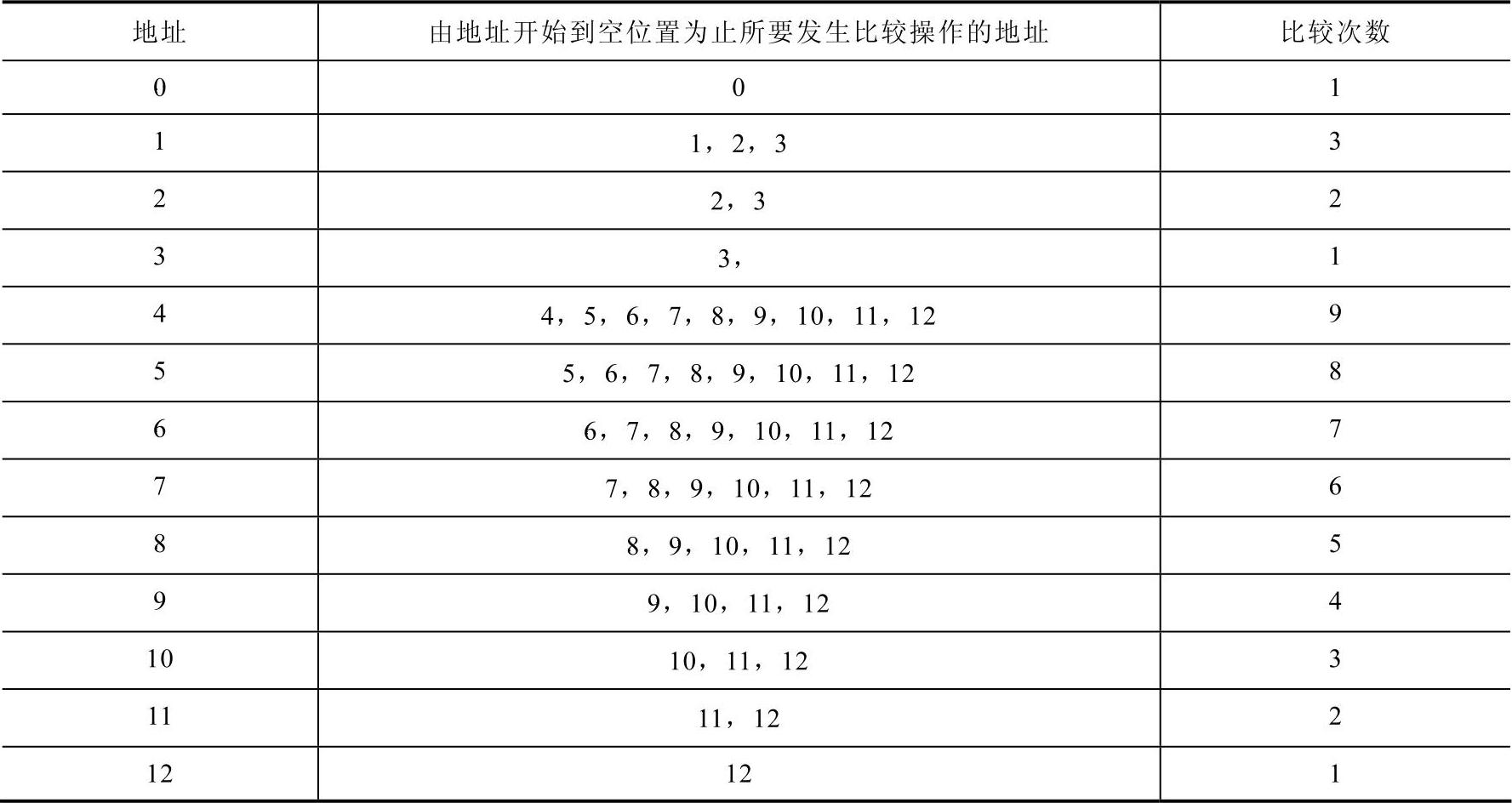
由以上分析并结合所求Hash表，可以得出表9-9。

表9-9 地址比较次数

(www.daowen.com)

由表9-9可知：

ASL₂=（1+3+2+1+9+8+7+6+5+4+3+2+1）/13=4

说明：在2）中查找不成功的情况下，可能多个关键字将被映射在同一个地址上，即说明这些关键字是属于同一类的，求比较次数的时候要以关键字所属的类为单位，而不是以单个关键字为单位。而关键字所属的类是用它们的Hash地址来区分的，类的个数就是Hash地址的个数，因此计算平均查找长度可以针对地址来计算。而1）中查找成功时的比较次数是针对各关键字来计算的，每个关键字计算出一个比较次数。这两种情况要注意区分。

注意：这里再次强调下，计算查找不成功的平均查找长度是根据Hash函数可以映射到的地址个数来计算的，而不是表内的所有地址，因为有些Hash函数的计算结果无法覆盖所有地址。例9-5只是一个特殊情况，如果将其Hash函数改为H（key）=key Mod 10，则其可映射到的地址范围变成0～9，10～12这些地址无法映射到。

说明：一般无特殊说明的情况下，Hash表中的空位置比较的次数也算在总比较次数之内。

在例9-5中，我们用到的Hash函数是用除留余数法来构造的，冲突是用开放定址法的线性探查法来解决的。除此之外，还有其他的构造方法和冲突解决方法，下面就介绍几种构造方法和冲突解决方法及其特点。

1.常用Hash函数的构造方法

（1）直接定址法

取关键字或关键字的某个线性函数为Hash地址，即H（key）=key或者H（key）=a×key+b，其中a和b为常数。

（2）数字分析法

假设关键字是r进制数（如十进制数），并且Hash表中可能出现的关键字都是事先知道的，则可选取关键字的若干数位组成Hash地址。选取的原则是使得到的Hash地址尽量减少冲突，即所选数位上的数字尽可能是随机的。

（3）平方取中法

取关键字平方后的中间几位作为Hash地址。通常在选定Hash函数的时候不一定能知道关键字的全部情况，仅取其中的几位为地址不一定合适，而一个数平方后的中间几位数和数的每一位都相关，由此得到的Hash地址随机性更大，取的位数由表长决定。

（4）除留余数法（本方法即为例9-5中所用到的方法）

取关键字被某个不大于Hash表表长m的数p除后所得的余数为Hash地址，即

H（key）=key mod p （p≤m）

在本方法中，p的选择很重要，一般p选择小于或者等于表长的最大素数，这样可以减少冲突。一般在综合应用题中往往会给出p，重点考查的是Hash表的建立和冲突的处理。

说明：在以上4种方法中，除留余数法在考研中涉及最多，考生要结合上述例题熟练掌握。

2.常用的Hash冲突处理方法

要注意的是，只可能尽量减少冲突的发生，而不可完全避免冲突。因此，在建立Hash表的时候必须进行冲突处理。假设Hash表是一个地址为0～m-1的顺序表，冲突是指由关键字得到的Hash地址j∈[0，…，m-1]处已存有记录，而冲突处理就是为该关键字的记录找到另一个空的Hash地址。在处理冲突的过程中，可能会得到一个地址序列H_i（H_i∈[0，…，m-1]，i=1，2，…，n），即冲突处理后所得到的另一个Hash地址H₁仍然发生冲突，只能再求下一个地址H₂，以此类推，直到H_n不发生冲突为止，H_n为记录在表中的Hash地址。

通常，处理冲突的方法有以下两种：

（1）开放定址法

在开放定址法中，以发生冲突的Hash地址为自变量，通过某种冲突解决函数得到一个新的空闲的Hash地址的方法有很多种，下面介绍两种考研中考查最多的方法。

1）线性探查法（本方法即为例9-5中所用到的方法）。线性探查法是从发生冲突的地址（设为d）开始，依次探查d的下一个地址（当到达下标为m-1的Hash表表尾时，下一个探查的地址是表首地址0），直到找到一个空位置为止，当m≥n（n是表中关键字的个数）时一定能找到一个空位置。线性探查法的递推公式为

H_i（k）=（H（k）+i）Modm（1≤i≤m-1）

线性探查法容易产生堆积问题。因为当连续出现若干同义词后，设第一个同义词占用单元d，这些连续的若干同义词将占用Hash表的d、d+1、d+2等单元，此时，随后任何d+1、d+2等单元上的Hash映射都会由于前面的同义词堆积而产生冲突，尽管所有的这些关键字并没有同义词。

2）平方探查法。设发生冲突的地址为d，则用平方探查法所得到的新的地址序列为d+1²，d-1²，d+2²，d-2²……平方探测法是一种较好的处理冲突的方法，可以减少出现堆积问题。它的缺点是不能探查到Hash表上的所有单元，但至少能探查到一半的单元。

此外，开放定址法的探查方法还有伪随机序列法以及双Hash函数法（双Hash法即Hash地址为H（H（k）））。

（2）链地址法

链地址法是把所有的同义词用单链表连接起来的方法。在这种方法中，Hash表每个单元中存放的不再是记录本身，而是相应同义词单链表的表头指针。通过例9-6可以体会到用这种方法的具体建表过程。