1.B-树关键字的查找

B-树关键字的查找很简单，是二叉排序树的扩展，二叉排序树是二路查找，B-树是多路查找。因为B-树结点内的关键字是有序的，在结点内进行查找的时候除了顺序查找之外，还可以用折半查找来提高效率。B-树的具体查找步骤如下（key为要查找的关键字）：

先让key与根结点中的关键字比较，如果key等于k[i]（k[]为结点内的关键字数组，如9.3.1节中结点结构所示），则查找成功。

若key＜k[1]，则到p[0]所指示的子树中进行继续查找（p[]为结点内的指针数组，如9.3.1节中结点结构所示）。

若key＞k[n]，则到p[n]所指示的子树中继续查找。

若k[i]＜key＜k[i+1]，则沿着指针p[i]所指示的子树继续查找。

如果最后遇到空指针，则证明查找不成功。

例如，在图9-10所示的B-树中查找关键字42。首先在根结点内查找，因为42＞30，则沿着根结点中指针p[1]往下走；在子树根中查找，因为39＜42＜45，则沿着子树根结点中指针p[1]往下走，在下层结点中查找关键字42成功，查找结束。

图9-10 在B-树中查找关键字42的路线

2.B-树关键字的插入和删除

下面通过例子来讲解B-树的插入和删除操作的一般方法。

【例9-4】 用以下关键字序列{1，2，6，7，11，4，8，13，10，5，17，9，16，20，3，12，14，18，19，15}创建一棵5阶B-树。对于该B-树，给出删除关键字8、16、15、4的过程。

分析：

与二叉排序树的建立一样，B-树的创建过程也是将关键字逐个插入到树中的过程。

在进行插入或者删除之前，要确定一下每个结点中关键字的个数范围，如果B-树的阶数为m，则结点中关键字个数的范围为m/2-1～m-1。

对于关键字的插入，需要找到插入位置。在B-树的查找过程中，当遇到空指针时，则证明查找不成功，同时也找到了插入位置，即根据空指针可以确定在最底层非叶结点中的插入位置，为了方便，以后我们称最底层的非叶结点为终端结点。由此可见，B-树新关键字的插入总是落在终端结点上。在插入过程中有可能破坏B-树的特性，如新关键字的插入使得结点中关键字的个数超出规定个数，这时要进行结点的拆分。

对于关键字的删除，需要找到待删除关键字。在结点中删除关键字的过程也有可能破坏B-树的特性，如旧关键字的删除可能使得结点中关键字的个数少于规定个数，这时可能需要向其兄弟结点借关键字或者和其孩子结点进行关键字的交换，也可能需要进行结点的合并。其中，和当前结点的孩子结点进行关键字交换的操作可以保证删除操作总是发生在终端结点上。

具体的操作步骤如下：

（1）求结点中关键字个数范围

由于题目要求建立5阶B-树，因此关键字个数的范围为2～4。

（2）关键字的插入

1）根结点最多可以容纳4个关键字，依次插入关键字1、2、6、7后的B-树如图9-11所示。

2）当插入关键字11的时候，发现此时结点中的关键字个数变为5，超出范围，则需拆分。取关键字数组的中间位置，即5/2=3处的关键字k[3]=6，独立作为一个结点，即新的根结点；将关键字6左、右的关键字分别做成两个结点，作为新根结点的两个分支（如上面提到的根结点不同于其他结点，可以只有两个分支）结点。此时B-树如图9-12所示。

图9-11 插入关键字1、2、 6、7后的结果

图9-12 插入关键字11后的结果

3）新关键字总是插入在终端结点上，插入关键字4、8、13后的B-树如图9-13所示。

4）关键字10需要插入在关键字8和11之间，此时又会出现关键字个数超出范围的情况，因此需要拆分。拆分时需要将关键字10并入根结点内，并将10左右的关键字做成两个新的结点连接在根结点上。插入关键字10并经过拆分操作后的B-树如图9-14所示。

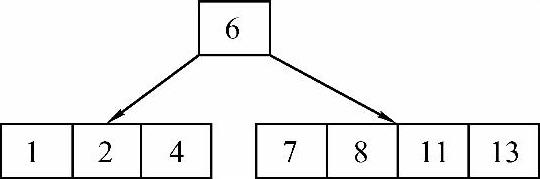
图9-13 插入关键字4、8、13后的结果

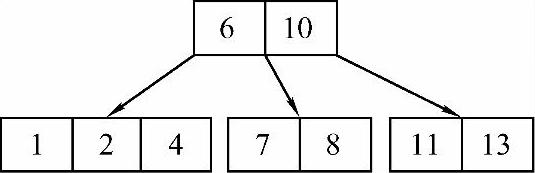
图9-14 插入关键字10后的结果

5）插入关键字5、17、9、16后的B-树如图9-15所示。

图9-15 插入关键字5、17、9、16后的结果

6）关键字20插入在关键字17之后，会造成结点关键字个数超出范围，需要拆分，方法同上。关键字20被插入后的B-树如图9-16所示。

图9-16 插入关键字20后的结果(www.daowen.com)

7）按照上述步骤将关键字3、12、14、18、19插入后的B-树如图9-17所示，在插入过程中也需要拆分操作。

图9-17 插入关键字3、12、14、18、19后的结果

8）插入最后一个关键字15。15应该插入到14之后，此时会出现关键字个数超出范围的情况，则需进行拆分，将13并入根结点；13并入后又使得根结点中关键字个数超出范围，需再次拆分，将10作为新的根结点，并将10左、右的关键字做成两个新结点连接到新根结点的指针上，这种插入一个关键字之后出现多次拆分的情况称为连锁反应。最终形成的B-树如图9-18所示。

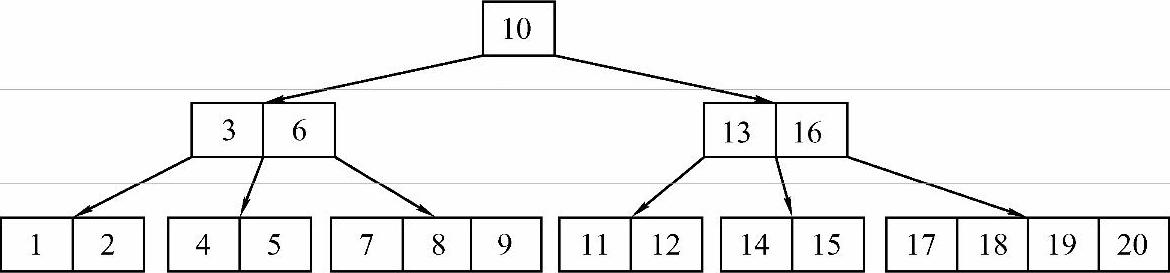
图9-18 插入关键字15后的结果

（3）结点的删除

1）删除关键字8、16。关键字8在终端结点上，并且删除后其所在结点中关键字的个数不会少于2，因此可以直接删除。关键字16不在终端结点上，可以用17来覆盖16，然后将原来的17删掉，这就是上面提到的和孩子结点进行关键字交换的操作。为什么不用15来覆盖16，然后删除原来的15呢？因为这样做会使15所在的结点中关键字的个数小于2，不满足B-树的规定。删除关键字8、16后的B-树如图9-19所示。

图9-19 删除关键字8、16后的结果

2）删除关键字15。15虽然也在终端结点上，但是不能直接删除，因为删除后当前结点中的关键字个数小于2。这时需要向其兄弟结点借关键字，显然应该向其右兄弟来借关键字，因为左兄弟的关键字个数已经是下限2。借关键字不能直接将右兄弟中的18移到15所在的结点上，因为这样会使得15所在的结点上出现了比17大的关键字，不满足B-树的规定。正确的借法应该是，先用17覆盖15，再用18覆盖原来的17，最后删除原来的18。删除关键字15后的B-树如图9-20所示。

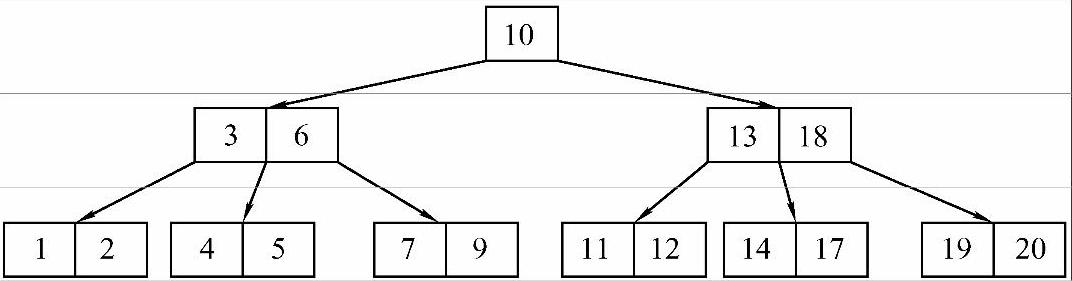
图9-20 删除关键字15后的结果

3）删除关键字4。此时4所在结点中关键字的个数已经是下限，需要借关键字，但其左、右兄弟结点的关键字数也都是下限，这里就要进行关键字的合并。可以先将关键字4删除，然后将关键字5、6、7、9合并为一个结点连接在关键字3右边的指针上，也可以将关键字1、2、3、5合并成一个结点连接在关键字6左边的指针上，此两种合并方法的局部图如图9-21所示，从图中可以看出，采用不同的合并方法将产生不同的B-树。

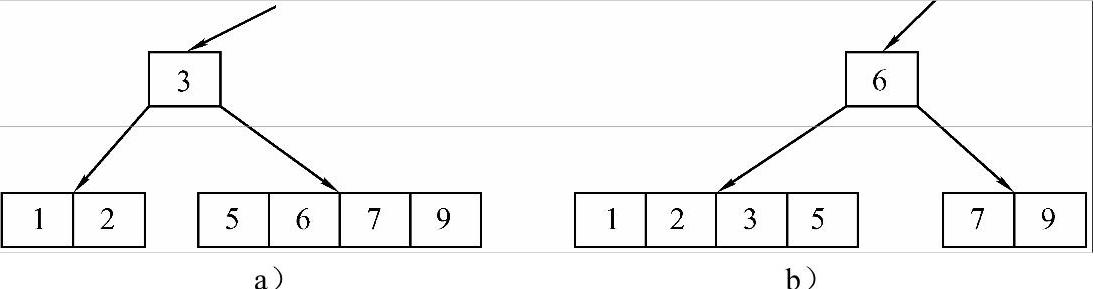
图9-21 不同方法产生不同的B-树

a）合并方法1 b）合并方法2

显然上述两种情况都已经不满足B-树的规定，即出现了非根的双分支结点，需要继续进行合并，沿着合并方法1的路线往下进行，将关键字3、10、13、18合并为一个新的结点，此时的B-树如图9-22所示。

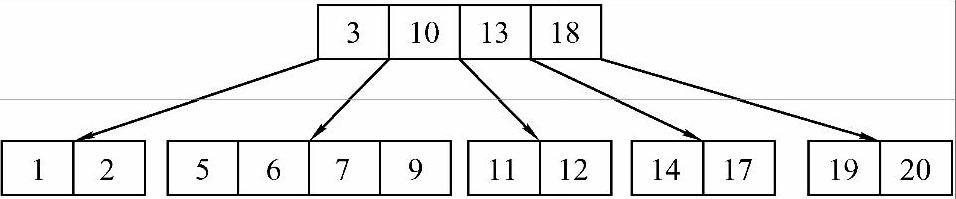
图9-22 删除关键字4后的结果

由上面这个例子可以总结出对于m阶的B-树的插入和删除的一般操作方法。

（1）插入操作

按照B-树的查找方法找到插入位置（插入位置一定出现在终端结点上），然后直接插入。插入后检查被插入结点内关键字的个数，如果关键字个数大于m-1，则需要进行拆分。进行拆分时，结点内的关键字若已经有m个，此时取出第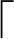m/2个关键字，并将第1～m/2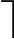-1个关键字和第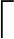m/2+1～m个关键字做成两个结点连接在第m/2个关键字左右的指针上，并将第m/2个关键字插入其父结点相应的位置中；如果在其父结点内又出现了关键字个数超出规定范围的情况，则继续进行拆分操作。插入操作只会使得B-树逐渐变高而不会改变叶子结点在同一层的特性。

（2）删除操作

1）如果要删除的关键字在终端结点上，这时有以下3种情况。

① 结点内的关键字个数大于m/2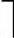-1，这时可以直接删除。

② 结点内的关键字个数等于m/2-1，并且其左、右兄弟结点中存在关键字个数大于m/2-1的结点，则从关键字个数大于m/2-1的兄弟结点中借关键字，过程如图9-23所示。

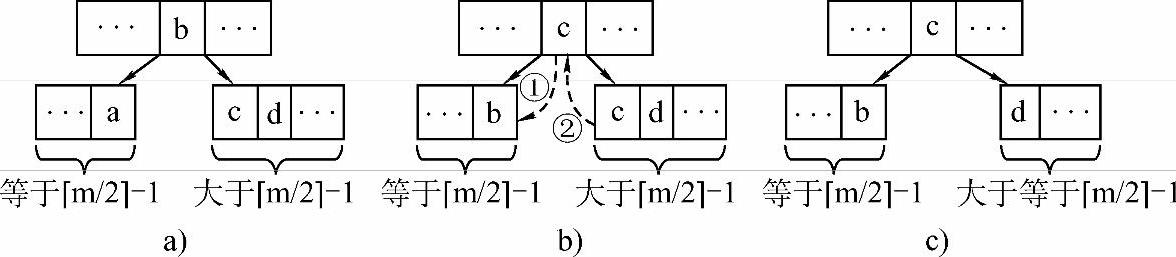
图9-23 删除关键字a的过程（a＜b＜c）

a）初始状态 b）关键字移动 c）删除原关键字c

③ 结点内的关键字个数等于m/2-1，并且其左、右兄弟结点中不存在关键字个数大于m/2-1的结点，这时需要进行结点的合并，过程如图9-24所示。

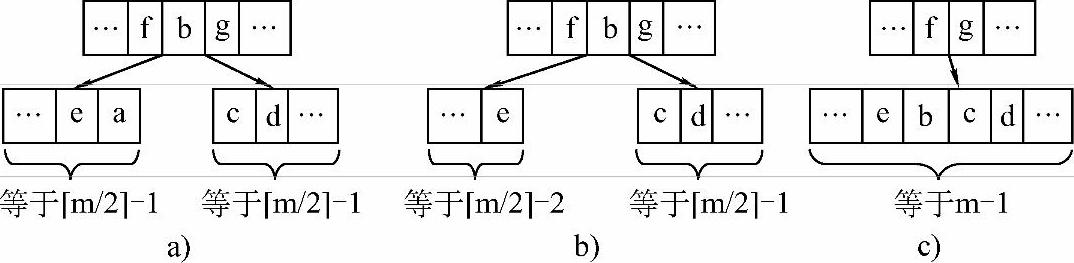
图9-24 删除关键字a后的结点合并过程（a＜b＜c）

a）初始状态 b）删除关键字a c）结点合并后

要注意的是，图9-24中删除关键字a后使得其父结点中的关键字减少一个，因此有可能使得其父结点中关键字个数少于规定个数，出现这种情况时要对其父结点继续进行合并操作。这就是由于删除结点引起的连锁反应。

2）如果要删除的关键字不在终端结点上，则需要先将其转化成在终端结点上，然后再按1）中所述方法进行处理。

在讲这种情况下的删除方法之前，要引入一个相邻关键字的概念，对于不在终端结点上的关键字a，它的相邻关键字为其左子树中值最大的关键字或者其右子树中值最小的关键字。找a的相邻关键字的方法为：沿着a的左指针来到其子树根结点，然后沿着根结点中最右端的关键字的右指针往下走，用同样的方法一直走到终端结点上，终端结点上的最右端的关键字即为a的相邻关键字（这里找到的是a左边的相邻关键字，找其右边的相邻关键字的方法类似）。这与二叉排序树中找一个关键字的前驱和后继的方法是类似的。如图9-25所示，a的相邻关键字是d和e。要删除关键字a，可以用d来取代a，然后按照1）中所述方法删除终端结点上的d即可（当然用e来取代a，之后删除e也可以）。

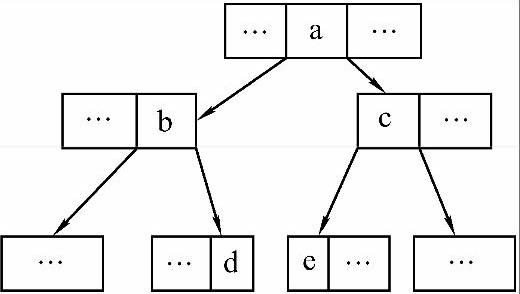
图9-25 a的相邻关键字为d和e