B-树中所有结点孩子结点个数的最大值称为B-树的阶,通常用m表示,从查找效率考虑,要求m≥3。一棵m阶的B-树或者是一棵空树,或者是满足以下要求的m叉树。
1)每个结点最多有m个分支(子树);而最少分支数要看是否为根结点,如果是根结点且不是叶子结点,则至少有两个分支,非根非叶结点至少有 m/2
m/2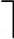 个分支(
个分支(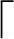 a
a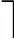 是对a向上取整,即不小于a的最小整数)。
是对a向上取整,即不小于a的最小整数)。
2)有n(k≤n≤m)个分支的结点有n-1个关键字,它们按递增顺序排列。k=2(根结点)或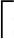 m/2
m/2 (非根结点)。
(非根结点)。
3)每个结点的结构为:

其中,n为该结点中关键字的个数;ki(1≤i≤n)为该结点的关键字且满足ki<ki+1;pi(0≤i≤n)为该结点的孩子结点指针且满足pi(1≤i≤n-1)所指结点上的关键字大于ki且小于ki+1,p0所指结点上的关键字小于k1,pn所指结点上的关键字大于kn。
4)结点内各关键字互不相等且按从小到大排列。
5)叶结点处于同一层;可以用空指针表示,是查找失败到达的位置。
扩展:平衡m叉查找树是指每个关键字的左侧子树与右侧子树的高度差的绝对值不超过1的查找树,其结点结构与上面提到的B-树结点结构相同。由此可见,B-树是平衡m叉查找树,但限制更强,要求所有叶结点在同一层。
注意:B-树的高度(深度),在不同的书上定义不同,主要区别在于是否把叶子结点层算在内,本书讨论高度的时候不包括叶子结点层。但如果已知一棵B-树的高度,要求结点数,则要把叶子结点算在内。如图9-9所示B-树高度为3,总结点数为30。
 (https://www.daowen.com)
(https://www.daowen.com)
图9-9 一棵5阶B-树
上面关于B-树的定义有点抽象,图9-9可以形象地帮你理解。
下面以图9-9为例来对上面B-树的5个特点逐条解释。
1)结点的分支数等于关键字数加1,最大的分支数就是B-树的阶数,因此m阶的B-树中结点最多有m个分支。通过图9-9可以看出,图中是一棵5阶B-树(这里的阶其实就是树的度)。
2)图9-9所示为一棵5阶B-树,因此 m/2
m/2 =
= 5/2
5/2 =3,可以看出,图中除了根结点外,所有的结点至少有3个分支。根结点可以不满足这个条件,图中根有两个分支。
=3,可以看出,图中除了根结点外,所有的结点至少有3个分支。根结点可以不满足这个条件,图中根有两个分支。
3)如果根结点中没有关键字就没有分支,此时B-树是空树;如果根结点有关键字,则其分支数必大于或等于2,因为分支数等于关键字数加1。
4)由图9-9可以看出,除根结点之外,结点中关键字的个数至少为2,因为分支数至少为3,分支数比关键字数多1;还可以看出结点内关键字都是有序的,并且在同一层上,左边结点内所有关键字均小于右边结点内的所有关键字。例如,第二层上的两个结点,左边结点内的关键字为15、26,它们均小于右边结点内的关键字39、45。
B-树中一个很重要的特性是,下层结点内的关键字取值总是落在由上层结点关键字所划分的区间内,具体落在哪个区间内可由指向它的指针看出。例如,图9-9中第二层最左边的结点内的关键字划分了3个区间:(-∞,15),(15,26),(26,+∞)。可以看出其下层中最左边结点内的关键字均落在(-∞,15)内,从左边数第二个结点内的关键字均落在(15,26)内。可以对照着图看出其他结点均满足这个规律。
5)图9-9中所示的B-树的叶子结点均在第4层上,代表查找不成功的位置(为了方便理解,本书将其简化为空指针,实际应用中此处指针指向一个结点,结点内设置一个标记代表查找不成功的位置,结点中还包含其他有用信息)。
注意:本节图中所示B-树中的关键字都是从左到右依次递增的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







