1.二叉排序树的定义与存储结构

（1）二叉排序树（BST）的定义

二叉排序树或者是空树，或者是满足以下性质的二叉树：

1）若它的左子树不空，则左子树上所有关键字的值均小于根关键字的值。

2）若它的右子树不空，则右子树上所有关键字的值均大于根关键字的值。

3）左右子树又各是一棵二叉排序树。

说明：由二叉排序树的定义可以知道，如果输出二叉排序树的中序遍历序列，则这个序列是递增有序的。

（2）二叉排序树的存储结构

二叉排序树通常采用二叉链表进行存储，其结点类型定义与一般的二叉树类似。

2.二叉排序树的基本算法

（1）查找关键字的算法

显然，要找的关键字要么在左子树上，要么在右子树上，要么在根结点上。由二叉排序树的定义可以知道，根结点中的关键字将所有关键字分成了两部分，即大于根结点中关键字的部分和小于根结点中关键字的部分。可以将待查关键字先和根结点中的关键字比较，如果相等则查找成功；如果小于则到左子树中去查找，无须考虑右子树中的关键字；如果大于则到右子树中去查找，无须考虑左子树中的关键字。如果来到当前树的子树根，则重复上述过程；如果来到了结点的空指针域，则说明查找失败。可以看出这个过程和折半查找法十分相似，实际上折半查找法的判定树就是一棵二叉排序树。

由此可以写出以下代码，算法中如果查找成功则返回关键字所在结点的指针，否则返回NULL。

微信答疑

提问：

上述程序中并列的两个return有什么实际意思？为什么用两个return？

回答：

上述程序中有返回值，返回值代表成功与否，return的作用是逐层将内部函数的返回值传给上层，最终由最外层函数返回，来告诉用户是否执行成功。(www.daowen.com)

（2）插入关键字的算法

二叉排序树是一个查找表，插入一个关键字首先要找到插入位置。对于一个不存在于二叉排序树中的关键字，其查找不成功的位置即为该关键字的插入位置，如图9-4所示。

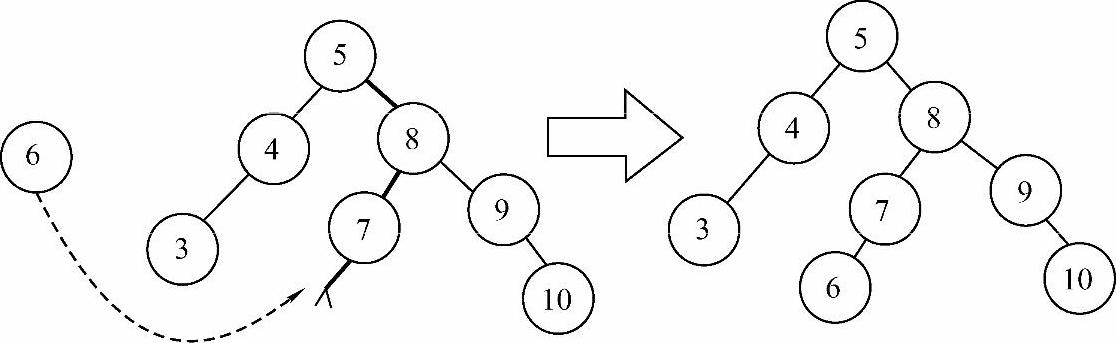
图9-4 在二叉排序树中插入关键字6的过程

因此只需对查找关键字的算法进行修改，在来到空指针的时候将关键字插入即可。在插入过程中如果待插入关键字已经存在，则返回0，代表插入不成功；如果待插入关键字不存在，则插入，并返回1，代表插入成功。算法实现代码如下：

说明：在二叉排序树中插入的关键字均存储在新创建的叶子上，由于找到的插入位置总是在空指针域上，因此在空指针域上连接的一个新结点必为叶子结点。

（3）二叉排序树的构造算法

掌握了二叉排序树的插入操作以后，二叉排序树的构造就变得非常简单。只需要建立一棵空树，然后将关键字逐个插入到空树中即可构造一棵二叉排序树。算法实现代码如下，假设关键字已经存入数组key[]中。

（4）删除关键字的操作

当在二叉排序树中删除一个关键字时，不能把以该关键字所在的结点为根的子树都删除，而是只删除这一个结点，并保持二叉排序树的特性。

假设在二叉排序树上被删除结点为p，f为其双亲结点，则删除结点p的过程分为以下3种情况。

1）p结点为叶子结点。由于删除叶子结点后不会破坏二叉排序树的特性，因此直接删除即可。

2）p结点只有右子树而无左子树，或者只有左子树而无右子树。此时只需将p删掉，然后将p的子树直接连接在原来p与其双亲结点f相连的指针上即可，如图9-5所示。

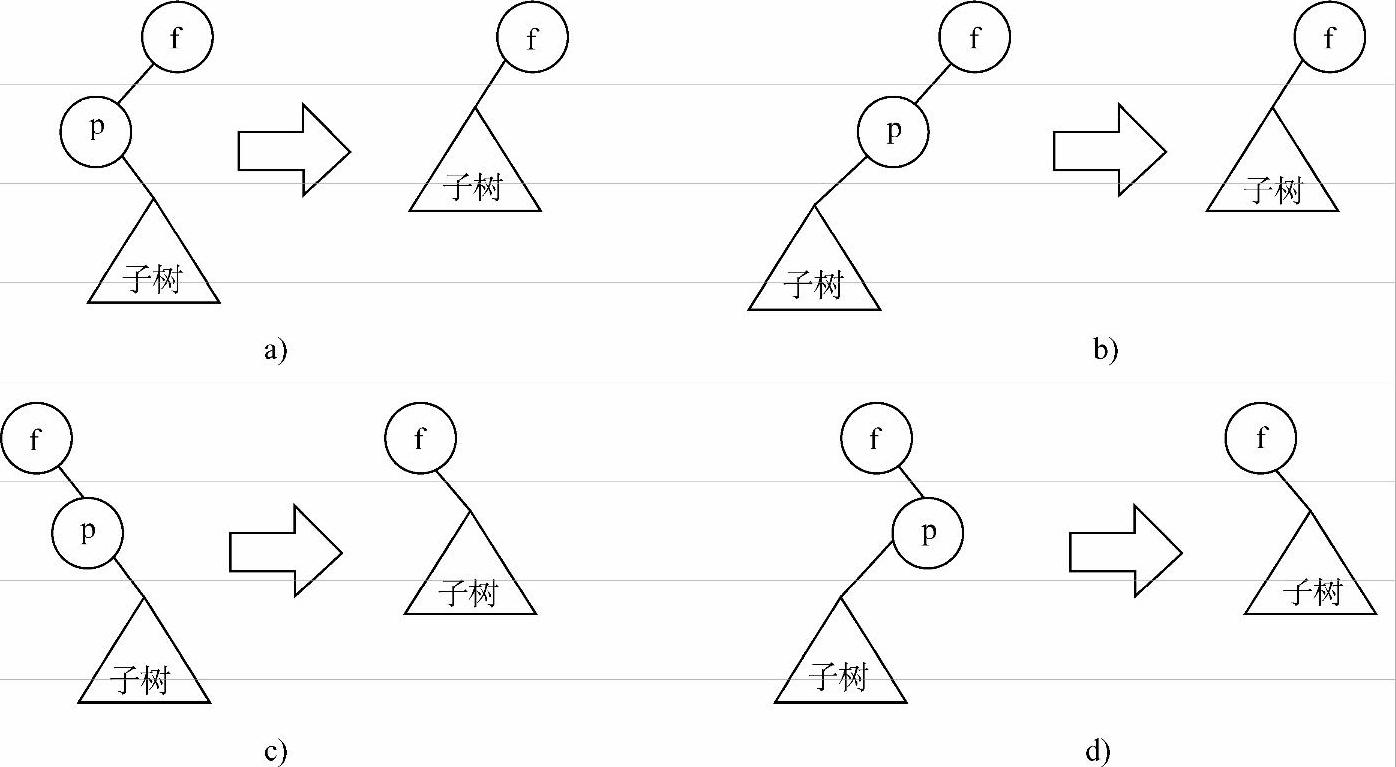
图9-5 被删结点p只有一棵子树的情况

3）p结点既有左子树又有右子树。此时可以将这种情况转化为1）或2）中的情况，做法为：先沿着p的左子树根结点的右指针一直往右走，直到来到其右子树的最右边的一个结点r（也可以沿着p的右子树根结点的左指针一直往左走，直到来到其左子树的最左边的一个结点）。然后将p中的关键字用r中的关键字代替。最后判断，如果r是叶子结点，则按照1）中的方法删除r；如果r是非叶子结点，则按照2）中的方法删除r（此时的r不可能是有两个子树的结点）。

说明：对于二叉排序树的删除操作应重点掌握其手工操作过程，即给一棵二叉排序树的简图，能画出删除其中任意一个关键字后的简图，这是考研的重点。因本算法代码考的可能性不高，考生应先熟练掌握手工操作过程，如果时间充裕再去掌握算法代码，算法代码严版课本上有，这里不再给出。