折半查找要求线性表是有序的，即表中记录按关键字有序（假设是递增有序的）。

折半查找的基本思路：设R[low，…，high]是当前的查找区间，首先确定该区间的中间位置mid=（low+high）/2；，然后将待查的k值与R[mid]比较，若相等，则查找成功，并返回该位置，否则需确定新的查找区间。若R[mid]＞k，则由表的有序性可知R[mid，…，high]均大于k，因此若表中存在关键字等于k的记录，则该记录必定是在mid左边的子表R[low，…，mid-1]中，故新的查找区间是左子表R[low，…，mid-1]。类似地，若R[mid]＜k，则要查找的k必在mid的右子表R[mid+1，…，high]中，即新的查找区间是右子表R[mid+1，…，high]。递归地处理新区间，直到子区间的长度小于1时查找过程结束。

算法如下：

折半查找的过程可以用二叉树来表示。把当前查找区间中的中间位置上的记录作为树根，左子表和右子表中的记录分别作为根的左子树和右子树，由此得到的二叉树称为描述折半查找的判定树。例如，对于序列{1，2，3，4，5，6，7，8，9，10，11}可以做出一棵判定树，如图9-1所示，图中叶子结点（方框所示）代表查找不成功的位置。由图9-1可知，折半查找的比较次数即为从根结点到待查找元素所经过的结点数，其比较次数最多的情况即为一直走到叶子结点的情况。因此，算法的时间复杂度可以用树的高度来表示。推广到一般情况，对于有n个记录的查找表，进行折半查找的时间复杂度为log₂n。折半查找的平均查找长度近似为log₂（n+1）-1，严版课本中有推导过程，了解但可不作重点。但是对于n为具体值的折半查找判定树的建立，以及平均查找长度的求法需要掌握，下面用一个例题来体会这个过程。

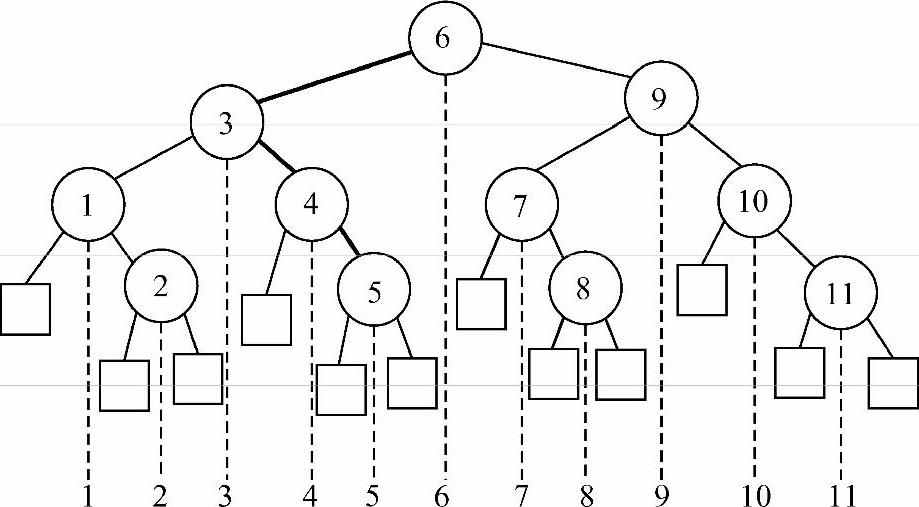
图9-1 折半查找判定树（查找5所走的路径）

【例9-2】 画出对于含有13个关键字的有序表进行折半查找的判定树，并分别求其在等概率查找表中元素时，查找成功和不成功的平均查找长度ASL₁、ASL₂。

分析：

本题的关键在于画出判定树，假设13个元素的有序表见表9-1。

表9-1 13个元素的有序表

根据表9-1建立判定树T1的过程如下：

1）确定T1中各结点在表中下标范围为0～12。

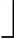2）由（0+12）/2=6可知，T1根结点为K7。T1左子树T2下标范围为0～5，右子树T3下标范围为7～12。

3）由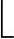（0+5）/2=2可知，T2根结点为K3。T2左子树T4下标范围为0～1，右子树T5下标范围为3～5。

4）由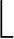（7+12）/2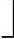=9可知，T3根结点为K10。T3左子树T6下标范围为7～8，右子树T7下标范围为10～12。(www.daowen.com)

5）由（0+1）/2=0可知，T4根结点为K1。T4左子树空，右子树只有一个结点K2，T4处理结束。

6）由（3+5）/2=4可知，T5根结点为K5。T5左子树只有一个结点K4，右子树也只有一个结点K6，T5处理结束。

7）由（7+8）/2=7可知，T6根结点为K8。T6左子树为空，右子树只有一个结点K9，T6处理结束。

8）由（10+12）/2=11可知，T7根结点为K12。T7左子树只有一个结点K11，右子树也只有一个结点K13，T7处理结束。

由1）～8）可绘制出图9-2所示的判定树，图中方框为空指针，代表查找不成功的位置。

查找成功的情况下，每个结点的比较次数见表9-2。

图9-2 折半查找判定树

表9-2 每个结点的比较次数

由此可知ASL₁=（3+4+2+4+3+4+1+3+4+2+4+3+4）/13=41/13。

查找不成功时，即各空指针处的比较次数见表9-3。

表9-3 空指针处的比较次数

由此可知ASL₂=（3+4+4+4+4+4+4+3+4+4+4+4+4+4）/14=27/7。

说明：一般无特殊说明的情况下，不把对空指针的比较次数计算在内。