顺序查找法是一种最简单的查找方法。它的基本思路是：从表的一端开始，顺序扫描线性表，依次将扫描到的关键字和给定值k比较，若当前扫描的关键字与k相等，则查找成功；若扫描结束后，仍未发现关键字等于k的记录，则查找失败。由以上可知，顺序查找法对于顺序表和链表都是适用的。对于顺序表，可以通过数组下标递增来顺序扫描数组中的各个元素；对于链表，则可通过表结点指针（假设为p）反复执行p=p-＞next；来扫描表中各个元素。

下面通过一个简单的例题来讲解一下本节和上一节内容的综合应用。

【例9-1】 数组a[]中有n个整数，没有次序，数组从下标1开始存储，请写出查找任一元素k的算法，若查找成功，则返回元素在数组中的位置；若查找不成功，则返回0。计算其平均查找长度以及算法的时间复杂度。

分析：

元素没有顺序，因此要扫描数组中的所有元素，逐个和k进行比较，相等时证明查找成功，返回元素位置；如果扫描结束时仍没有发现和k相等的元素，则查找不成功，返回0。

由此可以写出以下代码：(www.daowen.com)

由以上代码可知，根据k的不同取值，体现了两种查找长度：一种是查找成功的查找长度，另一种是查找失败的查找长度。ASL也有两种：一种是查找成功情况下的ASL₁，另一种是查找失败情况下的ASL₂。

对于第一种：p_i=1/n，c_i=i，因为若k等于a[i]，则在扫描到a[i]之前已经进行了i-1次比较，加上最后一次，一共进行了i次比较。

因此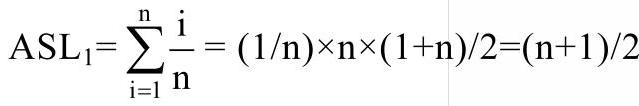

对于第二种：k在a[]中值之外的范围内取值，则查找不成功。这时候k的取值是无限的，但是对于k的任意一个取值，其查找长度必为n。根据上述代码中的if语句可以看出，对于所有的i值，a[i]==k都不成立，则循环必执行n次，即必有n次比较。因此ASL₂=n。

由ASL₁的表达式可以求出时间复杂度为O（n）。由ASL₂的表达式同样可以求出时间复杂度为O（n）。