1.时间复杂度

外部排序的时间复杂度涉及很多方面，且分析较为复杂，一般考试不会让考生分析整个流程中与时间复杂度相关的每一个细节，因此只需注意以下几点即可：

1）m个初始归并段进行k路归并，归并的趟数为log_km。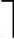

2）每一次归并，所有记录都要进行两次I/O操作。

3）置换-选择排序这一步中，所有记录都要进行两次I/O操作。

4）置换-选择排序中，选最值那一步的时间复杂度要根据考试要求的选择算法而定。

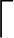5）k路归并的败者树的高度为log₂k+1，因此利用败者树从k个记录中选出最值需要进行log₂k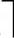次比较，即时间复杂度是O（log₂k）。(www.daowen.com)

6）k路归并败者树的建树时间复杂度为O（klog₂k）。

注意：k路归并败者树，不是k叉败者树，是一棵二叉树，且高度不包含最上层选出的结点，如图8-27中最上边的2结点。

说明：败者树和其他选择树的原理都是类似的，如之前堆排序中的堆。做法都是先用一个较大的时间复杂度将待排关键字建成一棵满足一定要求的树，然后就可以从中取出一个满足要求的关键字，并将新来的关键字放在刚取出的关键字的位置上。这样只会在一点上对树的结构造成破坏而不会造成全局的破坏，因此只需花较小的时间复杂度进行局部调整即可将被破坏的结构恢复正常，无须重新建树。局部调整即可恢复结构，从而降低时间复杂度，这就是选择树的精髓。

2.空间复杂度

显然所有步骤中的空间复杂度都是常量，因此是O（1）。