在k路归并中，若不使用败者树，则每次对读入的k个值需进行k-1次比较才能得到最值。引入败者树（由k个关键字构造成败者树）则每次不需要k-1次比较（除了第一次建树之外），只需要约log₂k次即可，因此在归并排序中选最值那一步常用败者树来完成。

败者树中含有两种不同类型的结点。

第一种：叶子结点，其值为从当前参与归并的归并段中读入的段首记录。叶子结点的个数为当前参与归并的归并段数，即k路归并叶子数为k。

第二种：非叶子结点，都是度为2的结点，其值为叶子结点的序号，同时也指示了当前参与选择的记录所在的归并段。

1.建立败者树

因树中有两种类型的结点，因此对其处理方法稍有不同，建树方法如下（以最小值败者树为例）：

1）对当前读入的k个记录，构造k个叶子结点，任意两个结点为一组，建二叉树，如果结点数不是偶数，则多余的那个结点放在下一趟处理。

2）如果当前参与建树的是两个叶子结点，则以败者（记录值较大者）所在归并段的序号构造新结点作为其父结点（T），胜者（记录值较小者）所在归并段的序号构造新结点作为T的父结点建一棵二叉树。

3）如果当前参与建树的两个结点是非叶根结点（必为单分支结点），则以败者（胜负关系通过结点中序号所指示的记录值大小判断）为这两个根结点子树的新根结点（T），胜者为T的父结点，建立一棵二叉树。

4）如果当前参与建树的两个结点一个是叶子结点，一个是非叶根结点，则有以下两种情况。

①如果叶子结点是胜者（胜负关系通过叶子结点记录值与非叶结点中序号所指示的记录值大小判断），则叶子结点挂在非叶根结点的空分支上，并以叶子结点记录值所在归并段序号构造新结点作为非叶根结点的父结点建一棵二叉树。

②如果叶子结点是败者，则以叶子结点记录值所在归并段序号构造新结点作为叶子结点和非叶根结点子树的新根结点（T），原非叶根结点作为T的父结点建一棵二叉树。

下面通过一个例题来体验一下此建树过程。

【例8-3】 有5个有序的归并段，段后数字为其序号，请以各段首记录建一棵最小值败者树。

F1：{17，21，…}，0

F2：{5，44，…}，1

F3：{10，12，…}，2

F4：{29，32，…}，3

F5：{15，56，…}，4

1）依次读取各归并段的第一个记录作为叶子结点：17、5、10、29、15，对应的序号依次为0、1、2、3、4。17和5相比，17为败者，5为胜者（小的为胜），则叶子结点17的下标0作为17和5的父结点，叶子结点5的下标1向上一级，成为下标0的父结点，如图8-20所示。

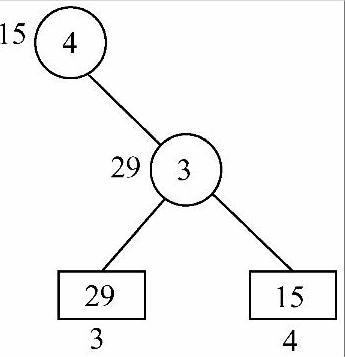
2）29和15相比，29为败者，15为胜者，则叶子结点29的下标3作为29和15的父结点，叶子结点15的下标4向上一级，成为下标3的父结点，如图8-21所示。

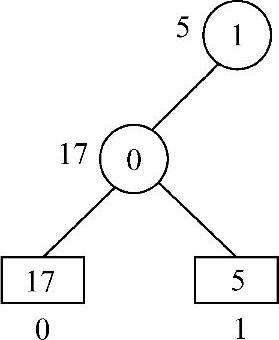
图8-20 17与5比较

(www.daowen.com)

图8-21 29与15比较

3）步骤1）中胜者5与第三个叶子结点10比较，10为败者，5为胜者，因此10的下标2替换到5的下标1的位置，5的下标1向上一级，成为下标2的父结点，如图8-22所示。

4）由步骤2）和步骤3）的中间结果开始，5与15比较，15为败者，5为胜者，则15的下标4取代5的下标1的位置，成为下标2和3的父结点，而5的下标1向上一级，成为下标4的父结点，如图8-23所示，得到最终败者树，得到最终胜者5，为当前最小值。

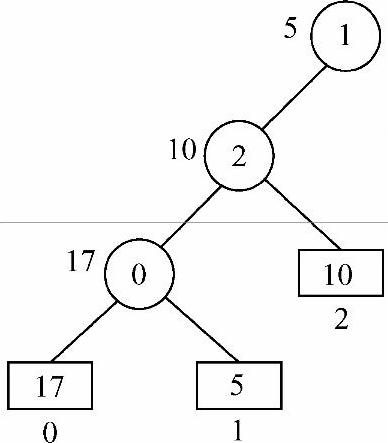
图8-22 10与5比较

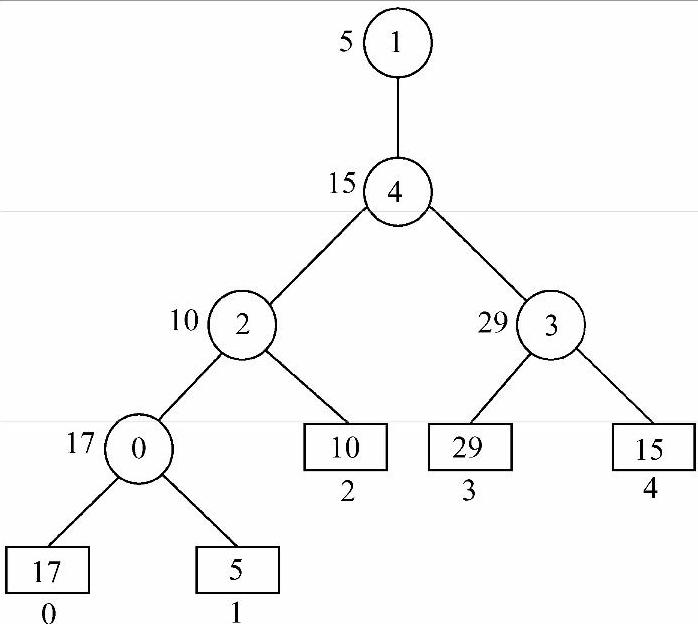
图8-23 最终得到的败者树

说明：可能有同学要问，这里为什么要以序号而不是记录值构造新结点？在下面的调整败者树中会给出答案。

2.调整败者树

从图8-23得到的败者树结果可知，来自序号为1的归并段的值为5的记录是当前选出的最小值记录，将会被存回外存。由此可以看出，由序号构造结点的好处是不仅可以找到记录值，还可以找到其所在的归并段，以便于下一个记录读入内存取代刚选出的最值。此时5被存回，用归并段1中的下一个值44来替换5，得到一棵待调整的败者树，如图8-24所示。

调整过程：

1）44和17比较，44败，17胜，因此44所在序号1作为两者父结点，17所在序号0作为1候选父结点，如图8-25方框内所示。

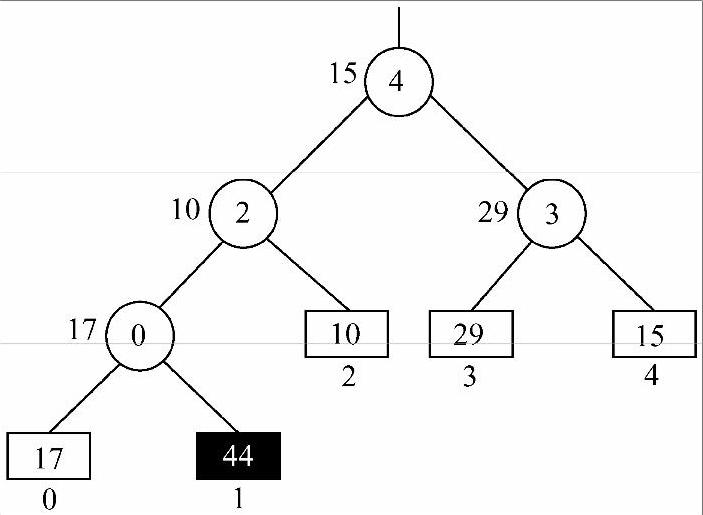
图8-24 待调整的败者树

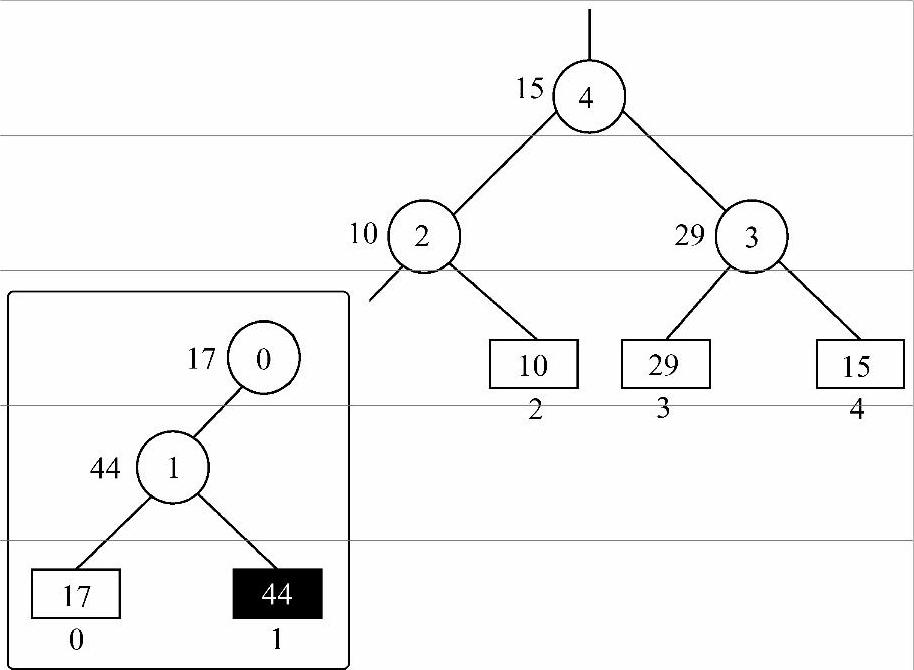
图8-25 调整中间过程，0为候选父结点，等待与2分出胜负

2）0和2比较，0败，2胜，因此0作为1和叶结点10的父结点，2作为0的候选父结点，如图8-26所示。

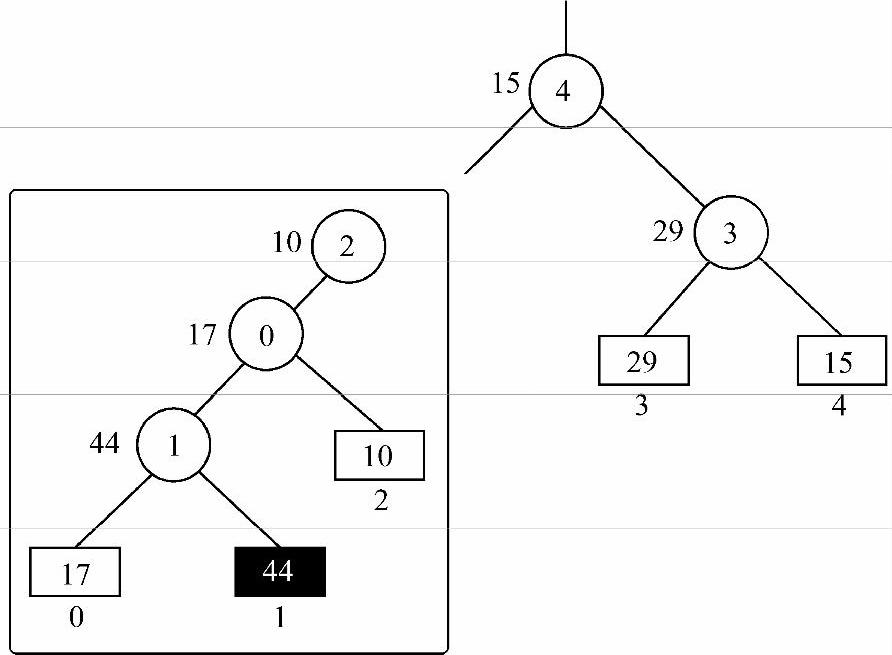
图8-26 调整中间过程，2为候选父结点，等待与4分出胜负

3）2和4比较，4败，2胜，因此4作为0和3的父结点，2作为根结点，得到最终调整结果，记录10为本次调整选出的最小值，如图8-27所示。

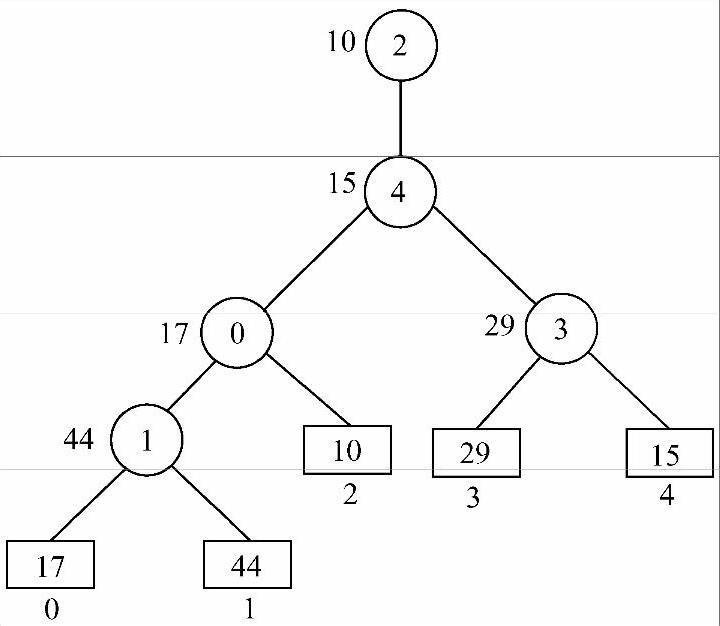
图8-27 调整结束，记录10为本次调整所选出的最小值