归并过程可以用一棵树来形象地描述，这棵树称为归并树，如图8-19即为一棵归并树，树中结点代表当前归并段长度。初始记录经过置换-选择排序之后，得到的是长度不等的初始归并段，归并策略不同，所得的归并树也不同，树的带权路径长度（带权路径长度与I/O次数的关系为：I/O次数=带权路径长度×2）也不同。为了优化归并树的带权路径长度，可将之前讲过的赫夫曼树运用到这里来，对于k路归并算法，可以用构造k叉赫夫曼树的方法来构造最佳归并树。

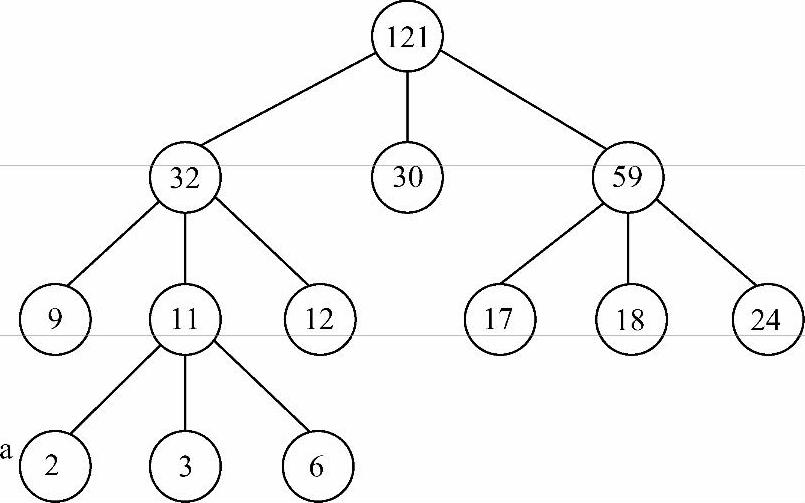
【例8-2】 设由置换-选择排序法得到9个初始归并段，其长度（记录个数）依次为9，30，12，18，3，17，2，6，24。请做出3-路归最佳归并树，并计算I/O次数。

解：仿照赫夫曼树的构造方法，可得3-路归最佳归并树，如图8-19所示。

(www.daowen.com)

图8-19 3-路归最佳归并树

I/O次数=2×（2×3+3×3+6×3+9×2+12×2+17×2+18×2+24×2+30×1）=446

说明：对于某初始归并段，其路径长度就等于其参加归并的次数。如图8-19中a结点代表的归并段，参加第一次归并进入长度为11的归并段，参加第二次归并进入长度为32的归并段，参加第三次归并进入最终归并段，共参加了3次归并，等于其路径长度3。a结点代表的归并段长度为2，即有两个记录，每个记录同样参加了3次归并，每次归并有两次I/O操作（入（I）算一次，出（O）算一次），因此对于a结点所代表的归并段，一共有2×3×2次I/O操作，同理可算出树中所有叶子结点代表的归并段总的I/O操作次数，结果同样也是整棵树的带权路径长度。