1.算法介绍

堆是一种数据结构，可以把堆看成一棵完全二叉树，这棵完全二叉树满足：任何一个非叶结点的值都不大于（或不小于）其左右孩子结点的值。若父亲大孩子小，则这样的堆叫作大顶堆；若父亲小孩子大，则这样的堆叫作小顶堆。

根据堆的定义知道，代表堆的这棵完全二叉树的根结点的值是最大（或最小）的，因此将一个无序序列调整为一个堆，就可以找出这个序列的最大（或最小）值，然后将找出的这个值交换到序列的最后（或最前），这样，有序序列关键字增加1个，无序序列中关键字减少1个，对新的无序序列重复这样的操作，就实现了排序。这就是堆排序的思想。

堆排序中最关键的操作是将序列调整为堆。整个排序的过程就是通过不断调整，使得不符合堆定义的完全二叉树变为符合堆定义的完全二叉树。

2.执行流程

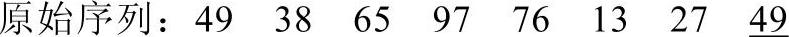
图8-1 原始序列对应的完全二叉树

（1）建堆

先将这个序列调整为一个大顶堆。原始序列对应的完全二叉树如图8-1所示。

在这个完全二叉树中，结点76、13、27、是叶子结点，它们没有左右孩子，所以它们满足堆的定义。从97开始，按97、65、38、49的顺序依次调整。

1）调整97。97＞49，所以97和它的孩子满足堆的定义，不需要调整。

2）调整65。65＞13，65＞27，所以65和它的孩子13、27满足堆的定义，不需要调整。

3）调整38。38＜97，38＜76，不满足堆定义了，需要调整。在这里，38的两个孩子结点值都比38大，应该和哪个交换呢？显然应该和两者中较大的交换，即和97交换。如果和76交换，则76＜97仍然不满足堆的定义。因此，将38和97交换。交换后38成了的根结点，38＜49，仍然不满足堆定义，需要继续调整，将38和交换，结果如图8-2所示。

4）调整49。49＜97，49＜65不满足堆定义，需要调整，找到较大的孩子97，将49和97交换。交换后49＜76仍不满足堆定义，继续调整，将49与76交换，结果如图8-3所示。

图8-2 调整38后的结果

图8-3 调整49后的结果

（2）插入结点

需要在插入结点后保持堆的性质，即完全二叉树形态与父大子小性质（以大顶堆为例），因此需要先将要插入的结点x放在最底层的最右边，插入后满足完全二叉树的特点；然后把x依次向上调整到合适位置以满足父大子小的性质。(www.daowen.com)

（3）删除结点

当删除堆中的一个结点时，原来的位置就会出现一个孔，填充这个孔的方法就是，把最底层最右边的叶子的值赋给该孔并下调到合适位置，最后把该叶子删除。

（4）排序可以看到，此时已经建立好了一个大顶堆。对应的序列为：97 76 65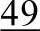 49 13 27 38。将堆顶关键字97和序列最后一个关键字38交换。第一趟堆排序完成。97到达其最终位置。将除97外的序列38 76 65 49 13 27重新调整为大顶堆。现在这个堆只有38是不满足堆定义的，其他的关键字都满足，所以只需要调整一个38就够了。

调整38，结果如图8-4所示。现在的序列为：76 65 38 49 13 27 97。将堆顶关键字76和最后一个关键字27交换，第二趟堆排序完成。76到达其最终位置，此时序列为：27 65 38 49 13 76 97。然后对除76和97的序列依照上面的方法继续处理，直到树中只剩1个结点时排序完成。

堆排序执行过程描述（以大顶堆为例）如下：

图8-4 再次调整38后的结果

1）从无序序列所确定的完全二叉树的第一个非叶子结点开始，从右至左，从下至上，对每个结点进行调整，最终将得到一个大顶堆。

对结点的调整方法：将当前结点（假设为a）的值与其孩子结点进行比较，如果存在大于a值的孩子结点，则从中选出最大的一个与a交换。当a来到下一层的时候重复上述过程，直到a的孩子结点值都小于a的值为止。

2）将当前无序序列中的第一个关键字，反映在树中是根结点（假设为a）与无序序列中最后一个关键字交换（假设为b）。a进入有序序列，到达最终位置。无序序列中关键字减少1个，有序序列中关键字增加1个。此时只有结点b可能不满足堆的定义，对其进行调整。

3）重复第2）步，直到无序序列中的关键字剩下1个时排序结束。

本算法代码如下：

3.性能分析

（1）时间复杂度分析

对于函数Sift（），显然j走了一条从当前结点到叶子结点的路径，完全二叉树的高度为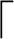log₂（n+1），即对每个结点调整的时间复杂度为O（log₂n）。对于函数heapSort（），基本操作总次数应该是两个并列的for循环中的基本操作次数之和，第一个循环的基本操作次数为O（log₂n）×n/2，第二个循环的基本操作次数为O（log₂n）×（n-1），因此整个算法的基本操作次数为O（log₂n）×n/2+O（log₂n）×（n-1），化简后得其时间复杂度为O（nlog₂n）。

（2）空间复杂度分析

算法所需的辅助存储空间不随待排序列规模的变化而变化，是个常量，因此空间复杂度为O（1）。

说明：上面对时间复杂度的分析不太严格，但是通过上面的方法去大体计算一个算法的时间复杂度，这在考研中运用得比较多，也符合考研对算法时间复杂度分析的要求。例如，一个算法中主要进行了在一棵完全二叉树中从某个结点走向叶子结点的操作，完全二叉树的高度为log₂（n+1），其时间复杂度就可以认为是O（log₂n），而不必十分严格地去考虑是从根结点出发到达叶子结点，还是从中间某个结点出发到达叶子结点。

堆排序在最坏情况下的时间复杂度也是O（nlog₂n），这是它相对于快速排序的最大优点。堆排序的空间复杂度为O（1），在所有时间复杂度为O（nlog₂n）的排序中是最小的，这也是其一大优点。堆排序适合的场景是关键字数很多的情况，典型的例子是从10000个关键字中选出前10个最小的，这种情况用堆排序最好。如果关键字数较少，则不提倡使用堆排序。