1.算法介绍

起泡排序又称冒泡排序。它是通过一系列的“交换”动作完成的。首先第一个关键字和第二个关键字比较，如果第一个大，则二者交换，否则不交换；然后第二个关键字和第三个关键字比较，如果第二个大，则二者交换，否则不交换……一直按这种方式进行下去，最终最大的那个关键字被交换到了最后，一趟起泡排序完成。经过多趟这样的排序，最终使整个序列有序。这个过程中，大的关键字像石头一样“沉底”，小的关键字像气泡一样逐渐向上“浮动”，起泡排序的名字由此而来。

2.算法流程

下面进行第一趟起泡排序。

1）1号和2号比较，49＞38，交换。

2）2号和3号比较，49＜65，不交换。

3）3号和4号比较，65＜97，不交换。

4）4号和5号比较，97＞76，交换。

5）5号和6号比较，97＞13，交换。

6）6号和7号比较，97＞27，交换。

7）7号和8号比较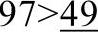，，交换。(www.daowen.com)

至此一趟起泡排序结束，最大的97被交换到了最后，97到达了它最后的位置。接下来对序列38 49 65 76 13 27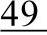按照同样的方法进行第二趟起泡排序。经过若干趟起泡排序后，最终序列有序。要注意的是，起泡排序算法结束的条件是在一趟排序过程中没有发生关键字交换。

起泡排序算法代码如下：

3.性能分析

（1）时间复杂度分析

由起泡排序算法代码可知，可选取最内层循环中的关键字交换操作作为基本操作。

1）最坏情况，待排序列逆序，此时对于外层循环的每次执行，内层循环中if语句的条件R[j]＜R[j-1]始终成立，即基本操作执行的次数为n-i。i的取值为1～n-1。因此，基本操作总的执行次数为（n-1+1）（n-1）/2=n（n-1）/2，由此可知时间复杂度为O（n²）。

2）最好情况，待排序列有序，此时内层循环中if语句的条件始终不成立，交换不发生，且内层循环执行n-1次后整个算法结束，可见时间复杂度为O（n）。

综合以上两种情况，平均情况下的时间复杂度为O（n²）。

（2）空间复杂度分析

由算法代码可以看出，额外辅助空间只有一个temp，因此空间复杂度为O（1）。