在AOE网中，从源点到汇点的所有路径中，具有最大路径长度的路径称为关键路径。完成整个工期的最短时间就是关键路径长度所代表的时间。关键路径上的活动称为关键活动。关键路径是个特殊的概念，它既代表了一个最短又代表了一个最长，它是图中的最长路径，又是整个工期所完成的最短时间。这句话的含义考生要好好理解。考研中所涉及本节的题目，主要是手工求关键路径的过程，下面通过一个例子总结求关键路径的一般方法。

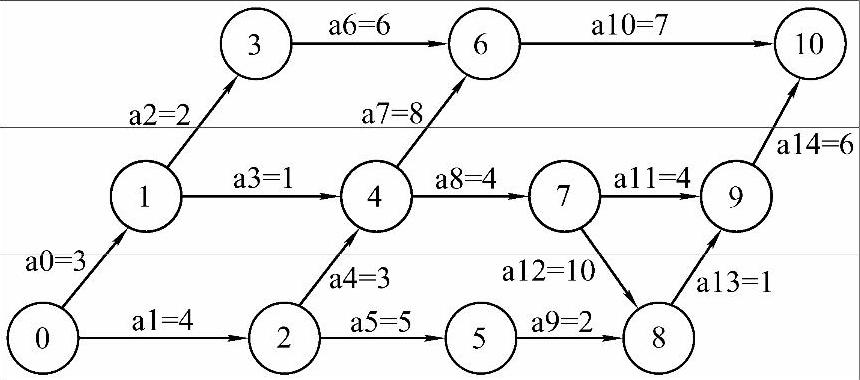
图7-27 AOE网

图7-27所示为一个AOE网，下面一步一步地求出它的关键路径，注意每一步的操作以及各步之间的联系。

1）设ve（k）为顶点k代表的事件（以下称事件k）的最早发生时间，即从源点到顶点k的路径中的最长者（注意下边求解过程中的max{}），即ve（k）为ve（j）+＜j，k＞权值后所得结果中的最大者，其中j为k的前驱事件，j可能有多个。为什么是最长者呢？因为在AOE网中，如果事件k要发生，必须在事件k之前的活动都已经完成的情况下才可能，k事件之前的活动是为k的发生做准备的；由源点到k的路径不止一条，每一条都代表为事件k的发生所做的准备工作，这些准备工作是同时开始进行的，显然k之前的所有准备工作的完成时间，可以用其中持续时间最长的准备工作的时间来表示，因此要取从源点到顶点k的路径中的最长者。在图7-27中，事件4的最早发生时间是路径＜0，2，4＞（长度为7）所代表的时间，而不是路径＜0，1，4＞（长度为4）所代表的时间。

为了求出关键路径，必须求出图中每个事件的最早发生时间，根据图7-27，具体过程如下：

① 对图7-27进行拓扑排序，得到各顶点的拓扑有序序列为0，1，2，3，4，5，6，7，8，9，10。

② 按照上述拓扑有序序列的顺序，依次求出各顶点所代表事件的最早发生时间。

初始时，将事件0的开始时间设置为0，即ve（0）=0。于是求得：

ve（1）=ve（0）+a0=0+3=3

ve（2）=ve（0）+a1=0+4=4

ve（3）=ve（1）+a2=3+2=5

ve（4）=max{ve（1）+a3，ve（2）+a4}=max{3+1，4+3}=7

ve（5）=ve（2）+a5=4+5=9

ve（6）=max{ve（3）+a6，ve（4）+a7}=max{5+6，7+8}=15

ve（7）=ve（4）+a8=7+4=11

ve（8）=max{ve（7）+a12，ve（5）+a9}=max{11+10，9+2}=21

ve（9）=max{ve（7）+a11，ve（8）+a13}=max{11+4，21+1}=22

ve（10）=max{ve（6）+a10，ve（9）+a14}=max{15+7，22+6}=28

2）设vl（k）为事件k的最迟发生时间，事件k的最迟发生时间是在不推迟整个工程完成的前提下，该事件最迟必须发生的时间。vl（k）为vl（j）-＜k，j＞权值后所得结果中的最小者（注意下边求解过程中的min{}），其中j为k的后继事件，j可能有多个。事件k的发生，一定不能推迟其所有后继事件的最迟发生时间，因此k要尽可能早地发生，而vl（j）-＜k，j＞所得结果越小表明k发生越早，因此要取其中的最小者。图7-27中的事件10是个特殊的事件，它的最早发生时间是整个工程的结束时间，因此它的最早发生时间也是最迟发生时间，即vl（10）=ve（10）。如果事件10推迟发生，则整个工程必定推迟完成。于是可以从顶点10开始逐一推算出其他事件的最迟发生时间，具体步骤如下：

① 对图7-27进行逆拓扑排序，得到各顶点的逆拓扑有序序列为10，9，6，8，5，7，3，4，1，2，0。

② 按照上述逆拓扑有序序列的顺序，依次求出各顶点所代表事件的最迟发生时间。

vl（10）=ve（10）=28

vl（9）=vl（10）-a14=28-6=22

vl（6）=vl（10）-a10=28-7=21

vl（8）=vl（9）-a13=22-1=21

vl（5）=vl（8）-a9=21-2=19

vl（7）=min{vl（9）-a11，vl（8）-a12}=min{22-4，21-10}=11

vl（3）=vl（6）-a6=21-6=15

vl（4）=min{vl（6）-a7，vl（7）-a8}=min{21-8，11-4}=7

vl（1）=min{vl（3）-a2，vl（4）-a3}=min{15-2，7-1}=6

vl（2）=min{vl（5）-a5，vl（4）-a4}=min{19-5，7-3}=4

vl（0）=min{vl（1）-a0，vl（2）-a1}=min{6-3，4-4}=0

3）由1）、2）两步，求出了图7-27中事件的最早和最迟发生时间。下面来求每个活动的最早和最迟发生时间。分别用e（ak）和l（ak）来表示当前活动ak的最早和最迟发生时间。图中的事件代表一个新活动的开始或旧活动的结束，因此事件的最早发生时间就是由这个事件所发出的活动的最早发生时间。活动的最迟发生时间怎样求得呢？我们知道图中事件的最迟发生时间代表了以它为结束点的活动的最迟结束时间，因此用事件的最迟发生时间减去以它为结束点的活动的持续时间，就得到活动的最迟发生时间。

由以上分析，可以求出各个活动的最早和最迟发生时间：

① 求最早发生时间。

e（a0）=e（a1）=ve（0）=0

e（a2）=e（a3）=ve（1）=3

e（a4）=e（a5）=ve（2）=4

e（a6）=ve（3）=5

e（a7）=e（a8）=ve（4）=7

e（a9）=ve（5）=9

e（a10）=ve（6）=15(www.daowen.com)

e（a11）=e（a12）=ve（7）=11

e（a13）=ve（8）=21

e（a14）=ve（9）=22

② 求最迟发生时间。

l（a0）=vl（1）-3=3

l（a1）=vl（2）-4=0

l（a2）=vl（3）-2=13

l（a3）=vl（4）-1=6

l（a4）=vl（4）-3=4

l（a5）=vl（5）-5=14

l（a6）=vl（6）-6=15

l（a7）=vl（6）-8=13

l（a8）=vl（7）-4=7

l（a9）=vl（8）-2=19

l（a10）=vl（10）-7=21

l（a11）=vl（9）-4=18

l（a12）=vl（8）-10=11

l（a13）=vl（9）-1=21

l（a14）=vl（10）-6=22

把①和②两步中所得数据整理成一个表，见表7-7。

表7-7 图7-27中活动的最早发生时间和最迟发生时间

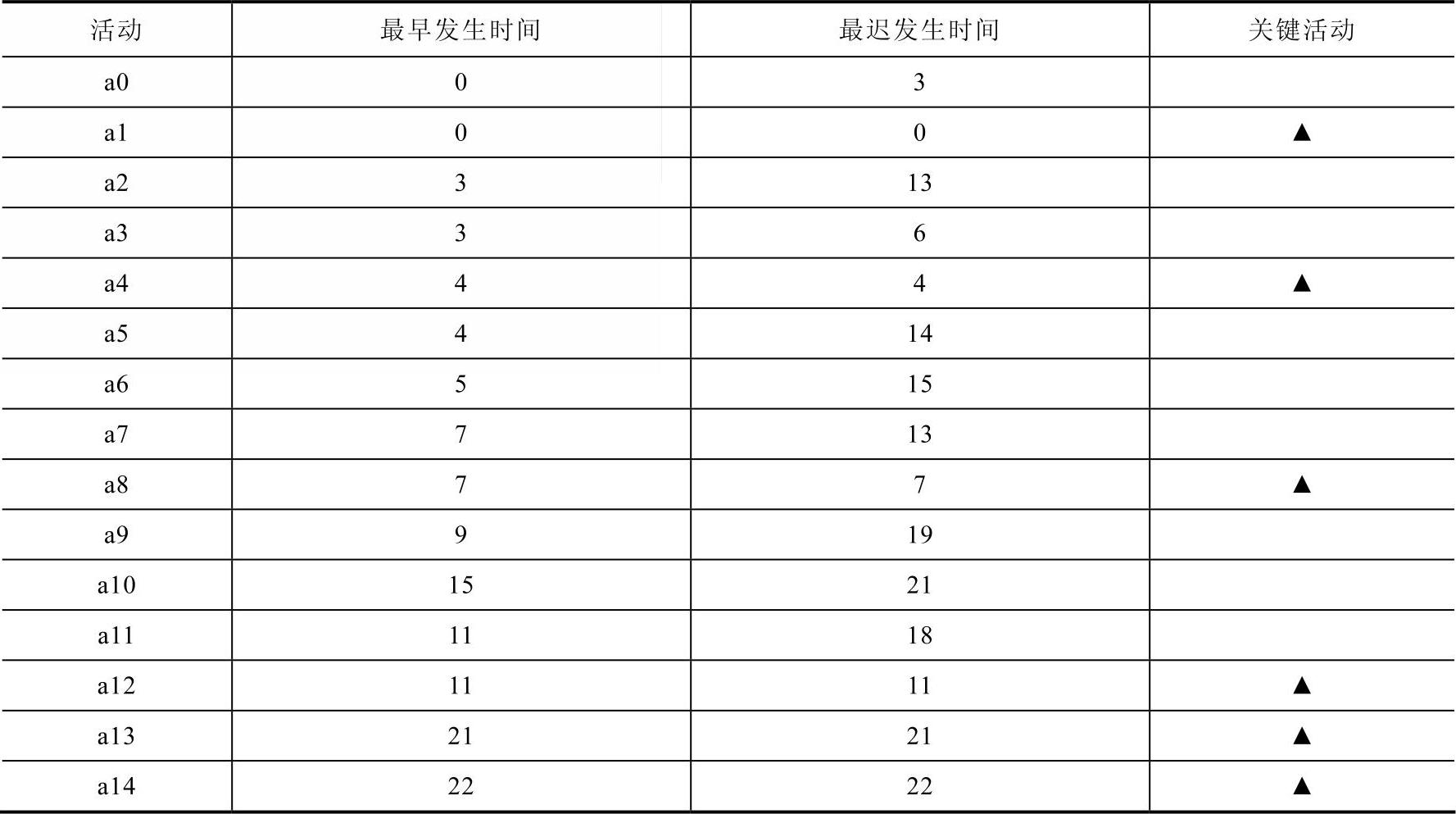
表7-7中用“▲”指出了关键活动，最早发生时间和最迟发生时间相同的活动就是关键活动。这里还要介绍一个量，就是活动的剩余时间。剩余时间等于活动的最迟发生时间减去活动的最早发生时间。剩余时间反映了活动完成的一种松弛度。例如，导师交给你一项任务，以你的水平可以3天完成，而导师给了你5天的时间，这样你就有2天的剩余时间。你只要在前两天内的任何一个时刻开始执行任务都不会影响最终任务的完成。通过表7-7可以看出，关键活动的剩余时间为0，这体现了关键活动在整个工程中的重要性，关键活动没有缓期执行的余地。关键活动组成了关键路径，本例中关键路径如图7-28所示。

由图7-28可知：a1+a4+a8+a12+a13+a14=28。

图7-28反映了关键路径所持续的时间就是整个工程所持续的时间。

说明：上述步骤写得比较详细，是为了方便大家理解。考试中如果出现这种手工求关键路径的题目大可不必这样写，大家可以在理解的基础上总结出适合自己的简洁的答题步骤。

由以上求解过程可以总结出求关键路径的一般方法，具体内容如下：

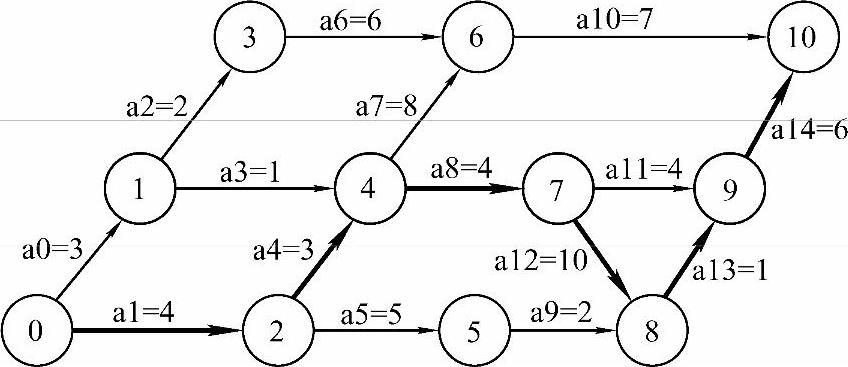
图7-28 关键路径

1）根据图求出拓扑有序序列a和逆拓扑有序序列b。

2）根据序列a和b分别求出每个事件的最早发生时间和最迟发生时间，求解方法如下：

① 一个事件的最早发生时间为指向它的边（假设为a）的权值加上发出a这条边的事件的最早发生时间。如果有多条边，则逐一求出对应的时间并选其中最大的结果作为当前事件的最早发生时间。

② 一个事件的最迟发生时间为由它所发出的边（假设为b）所指向的事件的最迟发生时间减去b这条边的权值。如果有多条边，则逐一求出对应的时间并选其中最小的结果作为当前事件的最迟发生时间。

3）根据2）中结果求出每个活动的最早发生时间和最迟发生时间。

4）根据3）中结果找出最早发生时间和最迟发生时间相同的活动，即为关键活动。由关键活动所连成的路径即为关键路径。

说明：考试中对于关键路径这一部分，可能出选择题，也可能出大题，只要根据上述讲解熟练掌握了关键路径的手工求解过程，无论是选择题还是大题，都可以迎刃而解。

微信答疑

提问：

一个工程的完成仅仅需要执行关键活动吗？还是说关键活动完成的同时其他普通活动也已经完成了呢？

回答：

不是的，图中所表示的所有活动都要执行，只不过关键路径执行所需的时间就是整个图中所有活动所完成的时间。

♥感觉本章算法很难理解？请扫描本书封面二维码，那里有详解视频，可能会对你的理解有帮助。