【例7-6】 分析本节中拓扑排序算法的时间复杂度。

分析：

本算法主体部分为一个单层循环和一个双重循环。单层循环执行次数为n。对于双重循环，直接根据循环条件分析循环执行的次数比较困难，故换个角度分析。首先看进栈操作，因为在无环情况下，每个结点恰好进栈一次，故进栈操作执行次数为n；其次分析入度减1操作，在无环情况下，当排序结束时，每个边恰好被逻辑删除一次，故入度减1操作的执行次数为e。因此，本算法中基本操作执行次数为n+n+e，因此时间复杂度为O（n+e）。

答：拓扑排序算法的时间复杂度为O（n+e），其中n为图中顶点个数，e为图中边的条数。

【例7-7】 求图7-26所示的一个拓扑有序序列，要求写出求解步骤。

解：

①由图7-26可知，入度为0的顶点为顶点0。输出0并删除其出度，得一新图；

②由新图可知，入度为0的顶点为顶点1、3。输出1并删除其出度，得一新图；

③由新图可知，入度为0的顶点为顶点2、3。输出3并删除其出度，得一新图；(www.daowen.com)

④由新图可知，入度为0的顶点为顶点2。输出2并删除其出度，得一新图；

⑤由新图可知，入度为0的顶点为顶点5。输出5并删除其出度，得一新图；

⑥由新图可知，入度为0的顶点为顶点4。输出4并删除其出度，得一新图；

⑦由新图可知，入度为0的顶点为顶点6。输出6并删除其出度，顶点全部输出，拓扑排序过程结束。

由以上步骤得拓扑有序序列为0，1，3，2，5，4，6。

说明：对于拓扑排序这一部分，重点掌握手工进行拓扑排序的过程（本节开始时讲的3步操作）。对于拓扑排序算法代码无须像最短路径算法代码那样当成模板来记忆使用，只需能够根据手工排序过程写出适合自己的代码即可。

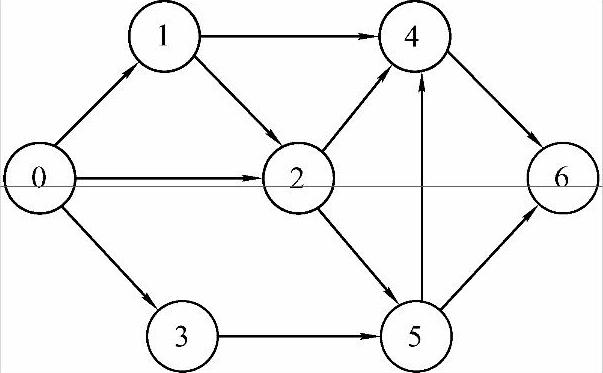
图7-26 例7-7图