迪杰斯特拉算法是求图中某一顶点到其余各顶点的最短路径，如果求图中任意一对顶点间的最短路径，则通常用弗洛伊德算法。

考试中涉及最多的是求用四阶方阵表示的图中每两点之间的最短路径的过程，方阵的阶数高了，计算量就比较大，考试中不会涉及太多。本算法的代码写起来要比迪杰斯特拉算法简单得多，因此在考试中，如果不对时间复杂度要求过于苛刻，尽量写本算法的代码，以减少错误。

对于本算法，需要掌握它的求解过程和程序代码，这两点比较简单，记住即可。对于考研要求，不需要钻研太多。下面就通过一个例子来总结用本算法求解最短路径的一般方法。

图7-24所示为一个有向图，各边的权值如图所示，用弗洛伊德算法求解其最短路径的过程如下。

对于图7-24，对应的邻接矩阵如下：

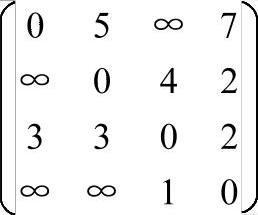
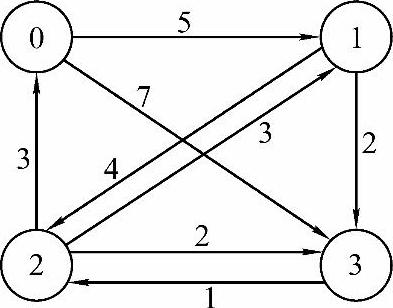
图7-24 有向图

初始时要设置两个矩阵A和Path，A用来记录当前已经求得的任意两个顶点最短路径的长度，Path用来记录当前两顶点间最短路径上要经过的中间顶点。

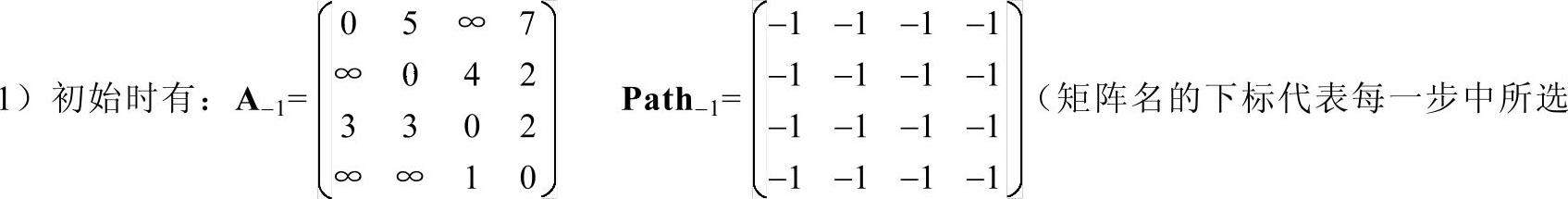
的中间顶点，图的顶点编号从0开始，初始的时候没有中间点，因此下标设为-1）。

2）以0为中间点，参照上一步矩阵中的结果，检测所有顶点对：{0，1}，{0，2}，{0，3}，{1，0}，{1，2}，{1，3}，{2，0}，{2，1}，{2，3}，{3，0}，{3，1}，{3，2}，假设当前所检测的顶点对为{i，j}，如果A[i][j]＞A[i][0]+A[0][j]，则将A[i][j]改为A[i][0]+A[0][j]的值，并且将Path[i][j]改为0。

经本次检测与修改，所得矩阵如下：

3）以1为中间点，参照上一步矩阵中的结果，检测所有顶点对，其中有A[0][2]＞A[0][1]+A[1][2]=5+4=9，因此将A[0][2]改为9，Path[0][2]改为1。

经本次检测与修改，所得矩阵如下：

4）以2为中间点，参照上一步矩阵中的结果，检测所有顶点对，其中有A[1][0]＞A[1][2]+A[2][0]=4+3=7，A[3][1]＞A[3][2]+A[2][1]=1+3=4，A[3][0]＞A[3][2]+A[2][0]=1+3=4，因此将A[1][0]改为7，将A[3][1]改为4，将A[3][0]改为4，将Path[1][0]、Path[3][0]和Path[3][1]都改为2。

经本次检测与修改，所得矩阵如下：

5）以3为中间点，参照上一步矩阵中的结果，检测所有顶点对，其中有A[0][2]＞A[0][3]+A[3][2]=7+1=8，A[1][0]＞A[1][3]+A[3][0]=2+4=6，A[1][2]＞A[1][3]+A[3][2]=2+1=3，因此将A[0][2]改为8，将A[1][0]改为6，将A[1][2]改为3，将Path[0][2]、Path[1][0]和Path[1][2]都改为3。(www.daowen.com)

经本次检测与修改，所得矩阵如下：

至此，得最终的矩阵A与Path如下：

由矩阵A可以查出图中任意两点间的最短路径长度。例如，要求顶点1到顶点3的最短路径长度，可查得A[1][3]为2。

由Path矩阵可以算出任意两点间最短路径上的顶点序列。例如，要求顶点1到顶点0最短路径上的顶点序列，可按照如下步骤进行。

① 由Path[1][0]=3可知，从顶点1到顶点0要经过顶点3，将3作为下一步的起点；

② 由Path[3][0]=2可知，从顶点3到顶点0要经过顶点2，将2作为下一步的起点；

③ 由Path[2][0]=-1可知，从顶点2有直接指向顶点0的边，求解结束。

由此得从顶点1到顶点0最短路径为1→3→2→0。

注意：细心的同学现在应该看出，上边输出两点间路径的步骤是一个递归的过程。反映其执行过程的伪代码如下：

从上述示例中可以总结出用弗洛伊德算法求解最短路径的一般过程，具体如下：

1）设置两个矩阵A和Path，初始时将图的邻接矩阵赋值给A，将矩阵Path中元素全部设置为-1。

2）以顶点k为中间顶点，k取0～n-1（n为图中顶点个数），对图中所有顶点对{i，j}进行如下检测与修改：

如果A[i][j]＞A[i][k]+A[k][j]，则将A[i][j]改为A[i][k]+A[k][j]的值，将Path[i][j]改为k，否则什么都不做。

由上述弗洛伊德算法求解最短路径的一般过程可写出以下弗洛伊德算法代码，其中定义两个二维数组A[][]和Path[][]，用来保存上述矩阵A和Path。

弗洛伊德算法的时间复杂度分析：

由算法代码可知，本算法的主要部分是一个三层循环，取最内层循环的操作作为基本操作，则基本操作执行次数为n³，因此时间复杂度为O（n³）。