通常采用迪杰斯特拉算法求图中某一顶点到其余各顶点的最短路径。

1.迪杰斯特拉算法思想

设有两个顶点集合S和T，集合S中存放图中已找到最短路径的顶点，集合T存放图中剩余顶点。初始状态时，集合S中只包含源点v₀，然后不断从集合T中选取到顶点v₀路径长度最短的顶点v_u并入到集合S中。集合S每并入一个新的顶点v_u，都要修改顶点v₀到集合T中顶点的最短路径长度值。不断重复此过程，直到集合T的顶点全部并入到S中为止。

在理解“集合S每并入一个新的顶点v_u，都要修改顶点v₀到集合T中顶点的最短路径长度值”的时候需要注意，在v_u被选入S中后，v_u被确定为最短路径上的顶点，此时v_u就像v₀到达T中顶点的中转站，多了一个中转站，就会多一些到达T中顶点的新的路径，而这些新的路径有可能比之前v₀到T中顶点的路径要短，因此需要修改原有v₀到T中其他顶点的路径长度。此时对于T中的一个顶点v_k，有两种情况：一种是v₀不经过v_u到达v_k的路径长度为a（旧的路径长度），另一种是v₀经过v_u到达v_k的路径长度为b（新的路径长度）。如果a≤b，则什么也不做；如果a＞b，则用b来代替a。用同样的方法处理T中其他顶点。当T中所有顶点都被处理完之后，会出现一组新的v₀到T中各顶点的路径，这些路径中有一条最短的，对应了T中一个顶点，就是新的v_u，将其并入S。重复上述过程，最后T中所有的顶点都会被并入S中，此时就可以得到v₀到图中所有顶点的最短路径。

2.迪杰斯特拉算法执行过程

引进3个辅助数组dist[]、path[]和set[]。

dist[v_i]表示当前已找到的从v₀到每个终点v_i的最短路径的长度。它的初态为：若从v₀到v_i有边，则dist[v_i]为边上的权值，否则置dist[v_i]为∞。

path[v_i]中保存从v₀到v_i最短路径上v_i的前一个顶点，假设最短路径上的顶点序列为v₀，v₁，v₂，…，v_i-1，vi，则path[vi]=vi_-1。path[]的初态为：如果v0到vi有边，则path[vi]=v₀，否则path[vi]=-1。

set[]为标记数组，set[v_i]=0表示v_i在T中，即没有被并入最短路径；set[v_i]=1表示v_i在S中，即已经被并入最短路径。set[]初态为：set[v₀]=1，其余元素全为0。

迪杰斯特拉算法执行过程如下：

1）从当前dist[]数组中选出最小值，假设为dist[v_u]，将set[v_u]设置为1，表示当前新并入的顶点为v_u。

2）循环扫描图中顶点，对每个顶点进行以下检测：

假设当前顶点为v_j，检测v_j是否已经被并入S中，即看是否set[v_j]=1。如果set[v_j]=1，则什么都不做；如果set[v_j]=0，则比较dist[v_j]和dist[v_u]+w的大小，其中w为边＜v_u，v_j＞的权值。这个比较就是要看v₀经过旧的最短路径到达v_j和v₀经过含有v_u的新的最短路径到达v_j哪个更短，如果dist[v_j]＞dist[v_u]+w，则用新的路径长度来更新旧的，并把顶点v_u加入路径中，且作为路径上v_j之前的那个顶点；否则什么都不做。

3）对1）和2）循环执行n-1次（n为图中顶点个数），即可得到v₀到其余所有顶点的最短路径。

迪杰斯特拉算法比较复杂，为便于理解，下面通过一个例子来体会一下用迪杰斯特拉算法求解最短路径的过程。

对图7-17中所示的有向图，用迪杰斯特拉算法求从顶点0到其余各顶点最短路径的过程如下。

初始态：dist[0]置0，dist[1]置4，dist[2]置6，dist[3]置6，其余元素置∞。

path[1]置0，path[2]置0，path[3]置0，其余元素置-1。

set[0]置1，其余元素置0。

假设图的邻接矩阵用二维数组g[][]表示，则g[i][j]为边＜i，j＞的权值。

1）从通往当前剩余顶点的路径中选出长度最短的，是0→1，长度为dist[1]=4，因此将顶点1并入最短路径中，set[1]置1，结果如图7-18所示。

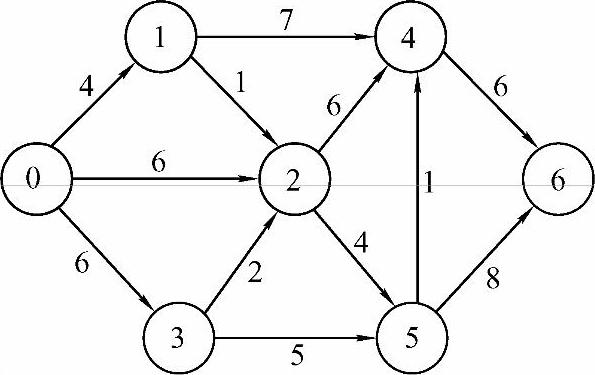
图7-17 初始态

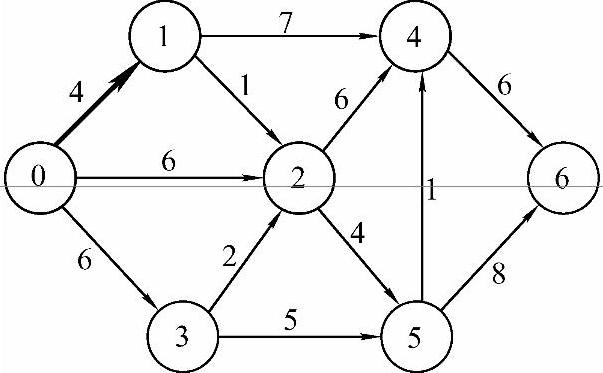
图7-18 结果1

以1为中间点检测剩余顶点{2，3，4，5，6}：

① dist[2]=6＞dist[1]+g[1][2]=5，因此dist[2]重置5，path[2]重置1。

② dist[3]=6＜dist[1]+g[1][3]=∞，因此dist[3]不变，path[3]不变。

③ dist[4]=∞＞dist[1]+g[1][4]=11，因此dist[4]重置11，path[4]重置1。

④ dist[5]=∞=dist[1]+g[1][5]=∞，因此dist[5]不变，path[5]不变。

⑤ dist[6]=∞=dist[1]+g[1][6]=∞，因此dist[6]不变，path[6]不变。

此时各数组值见表7-1。

2）从通往当前剩余顶点的路径中选出长度最短的，是0→1→2，长度为dist[2]=5，因此将顶点2并入最短路径中，set[2]置1，结果如图7-19所示。

以2为中间点检测剩余顶点{3，4，5，6}：

表7-1 以1为中间点检测剩余顶点时各数组值

注：表中方框内的数据代表本次检测中发生改变的数据。

① dist[3]=6＜dist[2]+g[2][3]=∞，因此dist[3]不变，path[3]不变；

② dist[4]=11=dist[2]+g[2][4]=11，因此dist[4]不变，path[4]不变；

③ dist[5]=∞＞dist[2]+g[2][5]=9，因此dist[5]重置9，path[5]重置2；

④ dist[6]=∞=dist[2]+g[2][6]=∞，因此dist[6]不变，path[6]不变。

此时各数组值见表7-2。

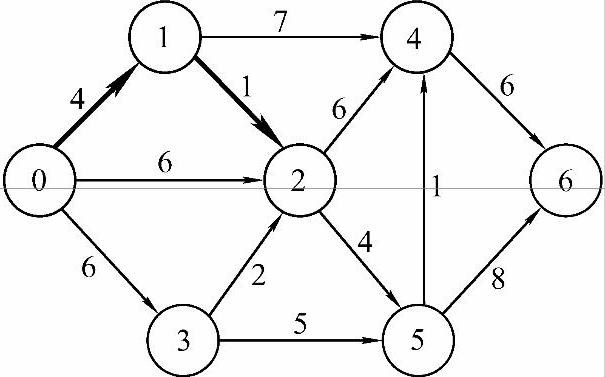
图7-19 结果2

表7-2 以2为中间点检测剩余顶点时各数组值

注：表中方框内的数据代表本次检测中发生改变的数据。

3）从通往当前剩余顶点的路径中选出长度最短的，是0→3，长度为dist[3]=6，因此将顶点3并入最短路径中，set[3]置1，结果如图7-20所示；

以3为中间顶点检测剩余顶点{4，5，6}：

① dist[4]=11＜dist[3]+g[3][4]=∞，因此dist[4]不变，path[4]不变；

② dist[5]=9＜dist[3]+g[3][5]=11，因此dist[5]不变，path[5]不变；

③ dist[6]=∞=dist[3]+g[3][6]=∞，因此dist[6]不变，path[6]不变。

此时各数组值见表7-3。

表7-3 以3为中间顶点检测剩余顶点时各数组值(www.daowen.com)

注：表中方框内的数据代表本次检测中发生改变的数据。

4）从通往当前剩余顶点的路径中选出长度最短的，是0→1→2→5，长度为dist[5]=9，因此将顶点5并入最短路径中，set[5]置1，结果如图7-21所示。

图7-20 结果3

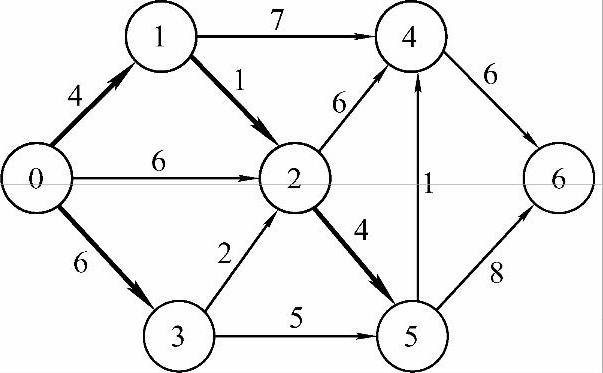
图7-21 结果4

以5为中间顶点检测剩余顶点{4，6}：

① dist[4]=11＞dist[5]+g[5][4]=10，因此dist[4]重置10，path[4]重置5；

② dist[6]=∞＞dist[5]+g[5][6]=17，因此dist[6]重置17，path[6]重置5。

此时各数组值见表7-4。

表7-4 以5为中间顶点检测剩余顶点时各数组值

注：表中方框内的数据代表本次检测中发生改变的数据。

5）从通往当前剩余顶点的路径中选出长度最短的，是0→1→2→5→4，长度为dist[4]=10，因此将顶点4并入最短路径中，set[4]重置1，结果如图7-22所示。

以4为中间顶点检测剩余顶点{6}：

dist[6]=17＞dist[4]+g[4][6]=16，因此dist[6]重置16，path[6]重置4。

此时各数组值见表7-5。

表7-5 以4为中间顶点检测剩余顶点时各数组值

注：表中方框内的数据代表本次检测中发生改变的数据。

6）从通往当前剩余顶点的路径中选出长度最短的，是0→1→2→5→4→6，长度为dist[6]=16，因此将顶点6并入最短路径中，set[6]重置1，结果如图7-23所示。

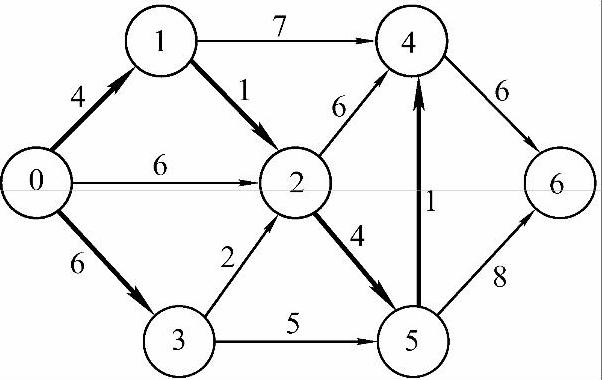
图7-22 结果5

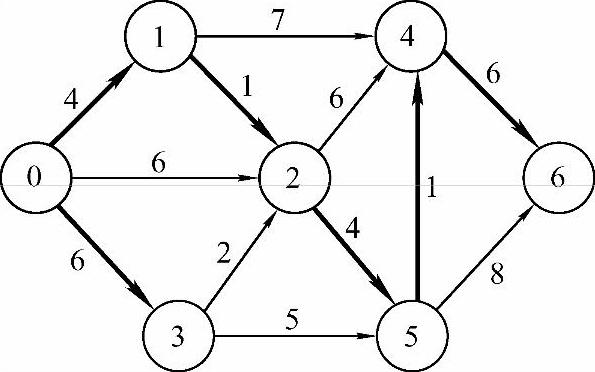
图7-23 结果6

此时所有顶点都已经并入最短路径中，求解过程结束。

此时各数组值见表7-6。

表7-6 所有顶点都并入最短路径时各数组值

注：表中方框内的数据代表本次检测中发生改变的数据。

由表7-6可知：

顶点0到顶点1的最短路径为0→1，长度为4。

顶点0到顶点2的最短路径为0→1→2，长度为5。

顶点0到顶点3的最短路径为0→3，长度为6。

顶点0到顶点4的最短路径为0→1→2→5→4，长度为10。

顶点0到顶点5的最短路径为0→1→2→5，长度为9。

顶点0到顶点6的最短路径为0→1→2→5→4→6，长度为16。

以上就是用迪杰斯特拉算法求最短路径的标准过程，考生务必在理解的基础上熟练掌握，这是考研中的重点。考研中很容易出像上边例子中的手工求解最短路径的题目，过程写得很详细，是为了方便考生理解。如果考研中遇到这样的题目，答卷的时候不必写得这么烦琐，你可以根据自己的理解提取出要点，总结出应对这类题目的答题模板。对于以上例子，下面这种写法是一种适合作为答案的简写方法。

解：

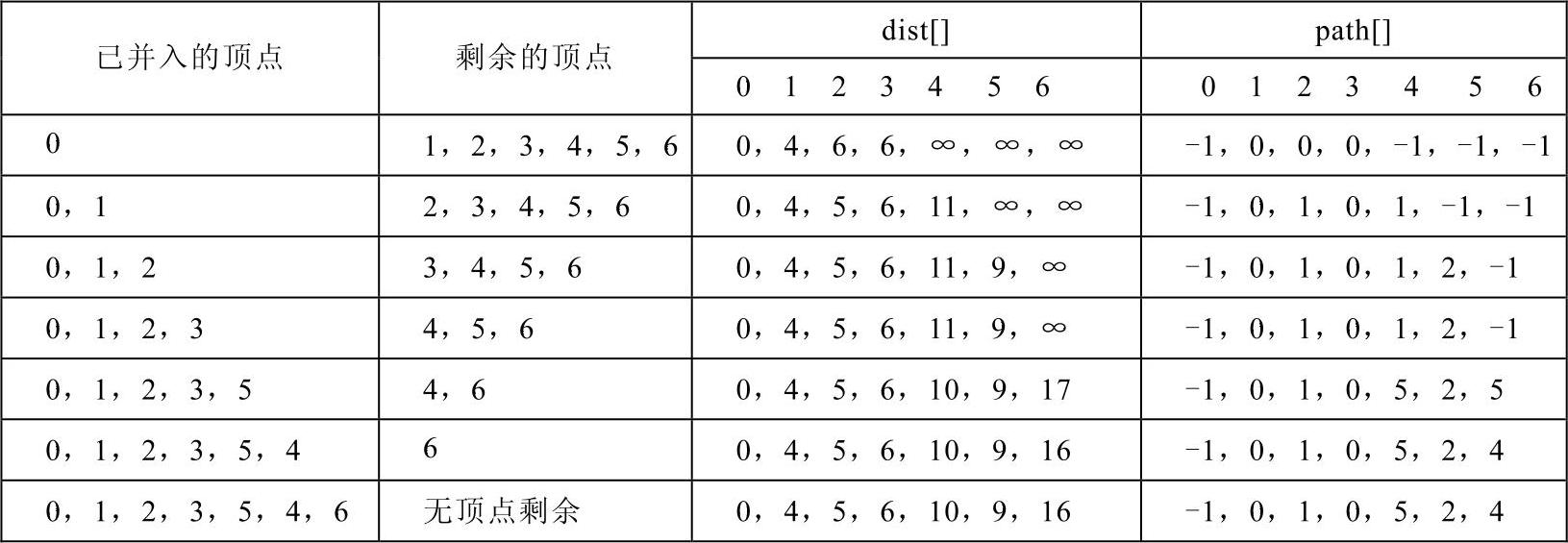
由上表可知，从顶点0到顶点1～6的最短路径长度分别为4，5，6，10，9，16。

此时的path[]数组为：

path[]数组中其实保存了一棵树，这是一棵用双亲存储结构存储的树，通过这棵树可以打印出从源点到任何一个顶点最短路径上所经过的所有顶点。树的双亲表示法只能直接输出由叶子结点到根结点路径上的结点，而不能逆向输出，因此需要借助一个栈来实现逆向输出，打印路径函数如下：

由上述讲解可以写出如下迪杰斯特拉算法代码：

3.迪杰斯特拉算法时间复杂度分析

由算法代码可知，本算法主要部分为一个双重循环，外层循环内部有两个并列的单层循环，可以任取一个循环内的操作作为基本操作，基本操作执行的总次数即为双重循环执行的次数，为n²次，因此本算法的时间复杂度为O（n²）。