【例7-4】 什么样的图其最小生成树是唯一的？

分析：

在构造最小生成树的过程中，要从剩余边中选择权值最小的并入当前生成树中，如果有多条边权值相同且同为最小值，则可任选其中一条边并入，这样就会产生多种最小生成树。要产生唯一一棵最小生成树，所有边的权值都为不相同的图才能满足条件。

答：在构造最小生成树时，如果图中所有边的权值均不相等，则其最小生成树是唯一的。

思考：一定要求图中所有边权值各不相同才能使生成树唯一吗？不一定，反例很好举，假如图G是一棵树（有n-1条边的连通图），它本身就是最小生成树，即使此图中所有边权值都相等，其最小生成树也是唯一的。对于此题，更为严谨的答案为：所有权值均不相等，或者有相等的边，但是在构造最小生成树的过程中权值相等的边都被并入生成树的图，其最小生成树唯一。

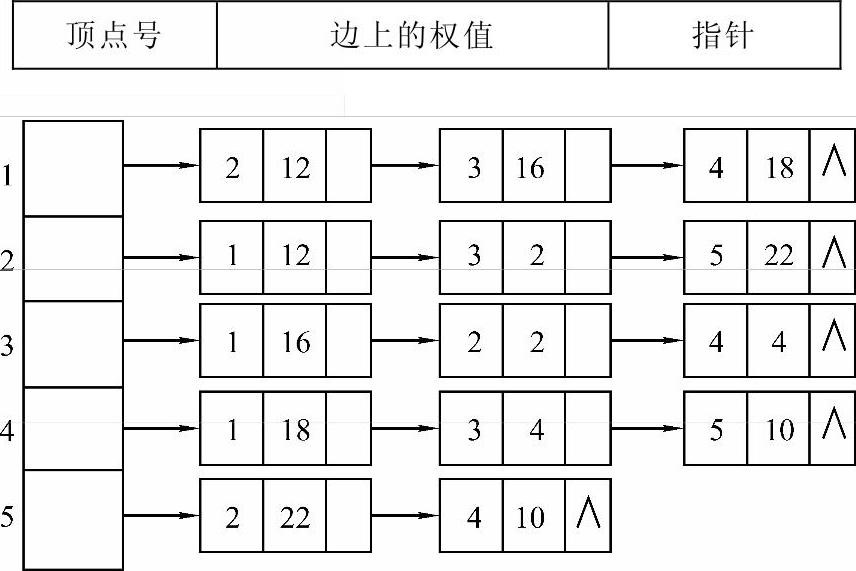
【例7-5】 已知带权连通图的邻接表表示如图7-14所示，请画出该图，并且分别以深度优先和广度优先遍历该图，写出遍历中结点的序列，并画出该图的一棵最小生成树。其中表结点的3个域分别为：

(www.daowen.com)

图7-14 图的邻接表

答：该图G如图7-15所示，从顶点1出发，深度优先遍历序列为1，2，3，4，5；广度优先遍历序列为1，2，3，4，5；最小生成树如图7-16所示。

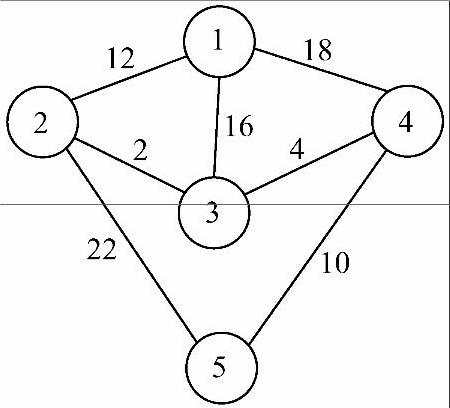
图7-15 无向图

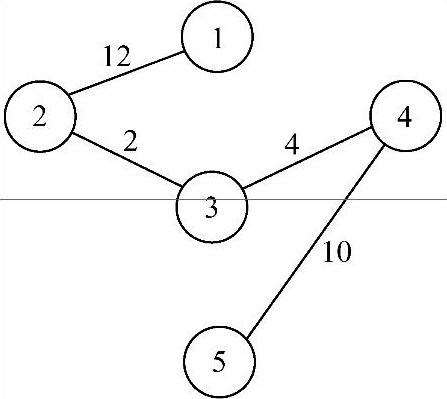
图7-16 最小生成树