1.普里姆算法

（1）普里姆算法思想

从图中任意取出一个顶点，把它当成一棵树，然后从与这棵树相接的边中选取一条最短（权值最小）的边，并将这条边及其所连接的顶点也并入这棵树中，此时得到了一棵有两个顶点的树。然后从与这棵树相接的边中选取一条最短的边，并将这条边及其所连顶点并入当前树中，得到一棵有3个顶点的树。以此类推，直到图中所有顶点都被并入树中为止，此时得到的生成树就是最小生成树。

例如，图7-10a所示的带权无向图采用普里姆算法求解最小生成树的过程如图7-10b～图7-10e所示，以顶点0为起点，生成树生成过程如下：

1）如图7-10a所示，此时候选边的边长分别为5、1和2，最小边长为1；

2）如图7-10b所示，选择边长为1的边，此时候选边的边长分别为5、3、2、6和2，其中最小边长为2；

3）如图7-10c所示，选择边长为2的边，此时候选边的边长分别为5、3、2和3，其中最小边长为2；

4）如图7-10d所示，选择边长为2的边，此时候选边的边长分别为3、4和5，其中最小边长为3；

5）如图7-10e所示，选择边长为3的边，此时所有顶点都已并入生成树中，生成树求解过程完毕。

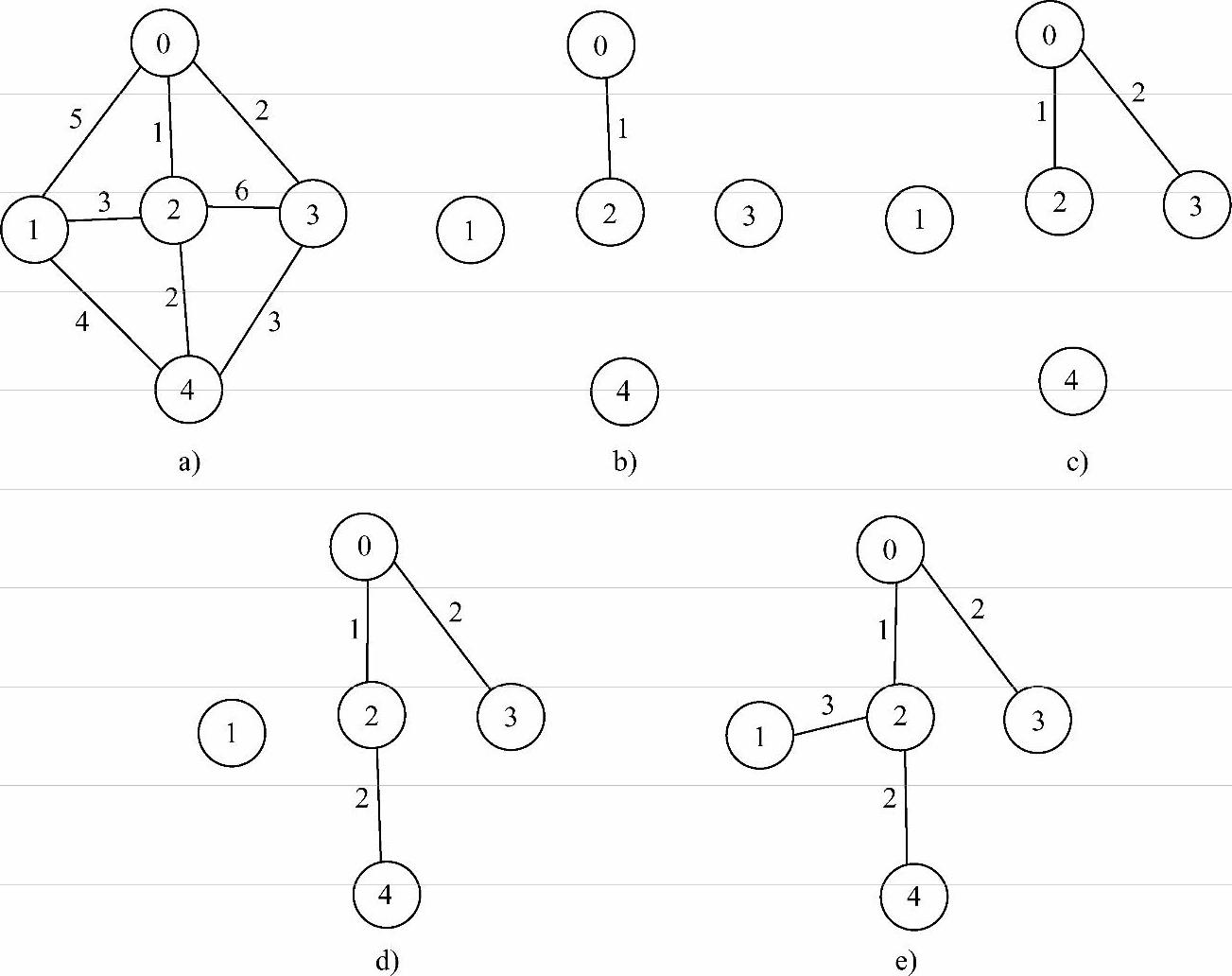
图7-10 普里姆算法求解最小生成树的过程

a）带权无向图 b）选择边长为1的边 c）选择边长为2的边 d）选择边长为2的边 e）选择边长为3的边

用普里姆算法构造最小生成树的过程中，需要建立两个数组vset[]和lowcost[]。vset[i]=1表示顶点i已经被并入生成树中，vset[i]=0表示顶点i还未被并入生成树中。lowcost[]数组中存放当前生成树到剩余各顶点最短边的权值。

说明：对“当前生成树到剩余各顶点最短边的权值”这句话的理解需要注意以下两点。

1）这句话说的是树这一整体到其余顶点的权值，而不是针对树中的某一顶点。

2）当前生成树到某一顶点可能有多条边。例如，对于顶点i，lowcost[i]中保存的是当前生成树到顶点i的多条边中最短的一条边的权值。lowcost[]中有多个最短边的权值，最短边条数对应于剩余顶点个数，已并入生成树的边不在考虑范围内。例如，在图7-11中，已并入树中的顶点为0、2、3，边为（0，2）、（0，3），剩余顶点为1、4。当前生成树到顶点4有两条边，最短的边为（2，4），权值为2，因此lowcost[4]=2；当前生成树到顶点1有两条边，最短的边为（2，1），权值为3，因此lowcost[1]=3。

图7-11 当前生成树到其余顶点的最短边

（2）普里姆算法执行过程

从树中某一个顶点v₀开始，构造生成树的算法执行过程如下：

1）将v₀到其他顶点的所有边当作候选边；

2）重复以下步骤n-1次，使得其他n-1个顶点被并入到生成树中。

①从候选边中挑选出权值最小的边输出，并将与该边另一端相接的顶点v并入生成树中；

②考查所有剩余顶点v_i，如果（v，v_i）的权值比lowcost[v_i]小，则用（v，v_i）的权值更新lowcost[v_i]。

普里姆算法代码如下：(www.daowen.com)

说明：形参写成MGraphg会使参数传入因复制了一个较大的变量而变得低效，不过考研中一般不考虑这些。关于“用引用型避免函数参数复制”的问题讲解请读者自行查找相关资料。

（3）普里姆算法时间复杂度分析

观察算法代码，普里姆算法主要部分是一个双重循环，外层循环内有两个并列的单层循环，单层循环内的操作都是常量级的，因此可以取任一个单层循环内的操作作为基本操作。例如，取min=lowcost[j]；这一句作为基本操作，其执行次数为n²，因此普里姆算法的时间复杂度为O（n²）。可见普里姆算法的时间复杂度只与图中顶点有关系，与边数没有关系，因此普里姆算法适用于稠密图。

2.克鲁斯卡尔算法

（1）克鲁斯卡尔算法思想

每次找出候选边中权值最小的边，就将该边并入生成树中。重复此过程直到所有边都被检测完为止。

说明：克鲁斯卡尔算法思想较为简单，因此在考研中需要手工构造生成树时，一般多用此方法。图7-12所示为用克鲁斯卡尔方法求图的最小生成树的过程。

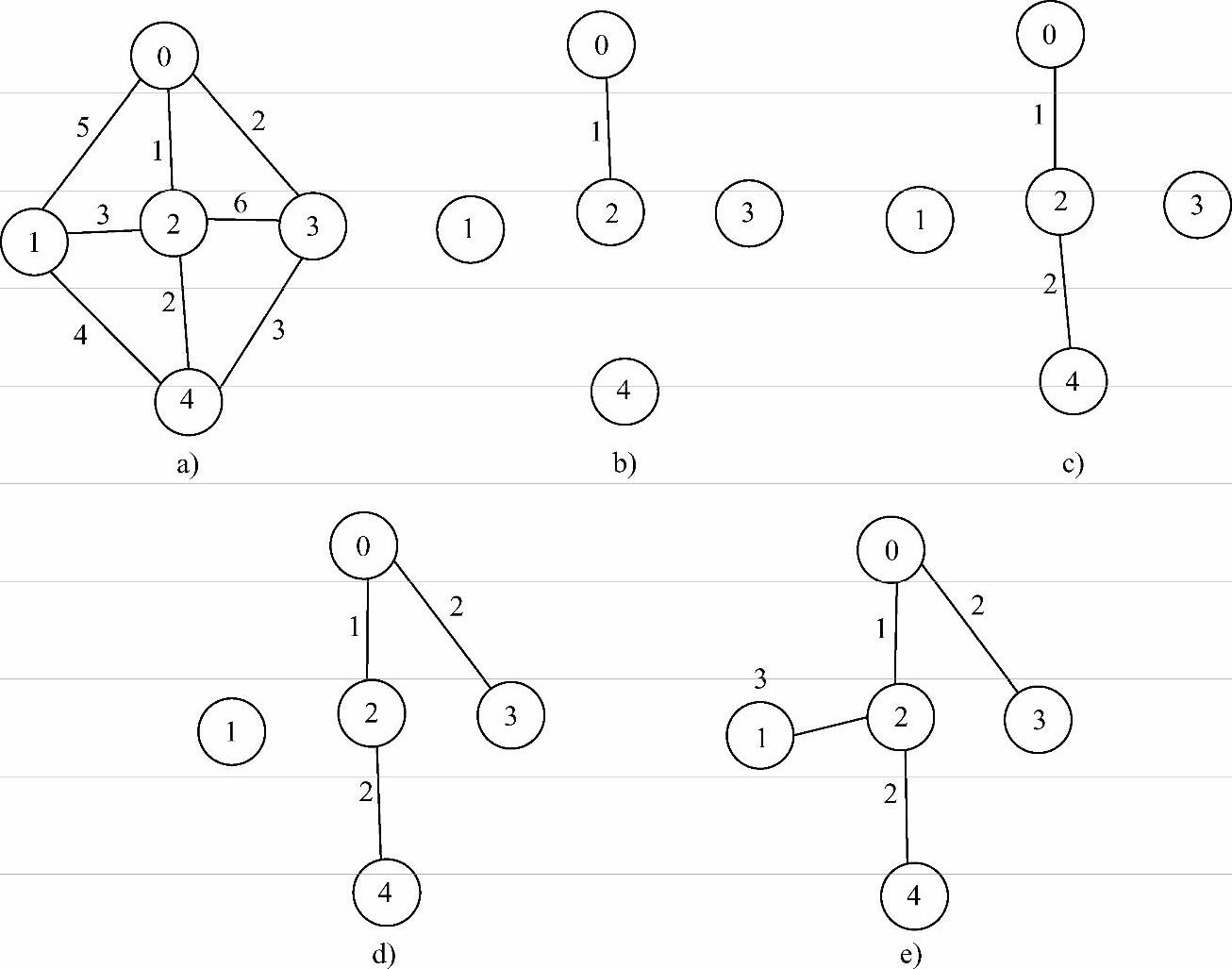
图7-12 克鲁斯卡尔算法求解最小生成树的过程

a）原图 b）引入第1条边 c）引入第2条边 d）引入第3条边 e）引入第4条边，生成树构建完成

（2）克鲁斯卡尔算法的执行过程

将图中边按照权值从小到大排序，然后从最小边开始扫描各边，并检测当前边是否为候选边，即是否该边的并入会构成回路，如不构成回路，则将该边并入当前生成树中，直到所有边都被检测完为止。

判断是否产生回路要用到并查集，关于并查集只介绍它在本算法中的应用。并查集中保存了一棵或者几棵树，这些树有这样的特点：通过树中一个结点，可以找到其双亲结点，进而找到根结点（其实就是之前讲过的树的双亲存储结构）。这种特性有两个好处：一是可以快速地将两个含有很多元素的集合并为一个。两个集合就是并查集中的两棵树，只需找到其中一棵树的根，然后将其作为另一棵树中任何一个结点的孩子结点即可。二是可以方便地判断两个元素是否属于同一个集合。通过这两个元素所在的结点找到它们的根结点，如果它们有相同的根，则说明它们属于同一个集合，否则属于不同集合。并查集可以用一维数组来简单地表示。图7-13所示即为并查集在数组中的表示及合并过程。

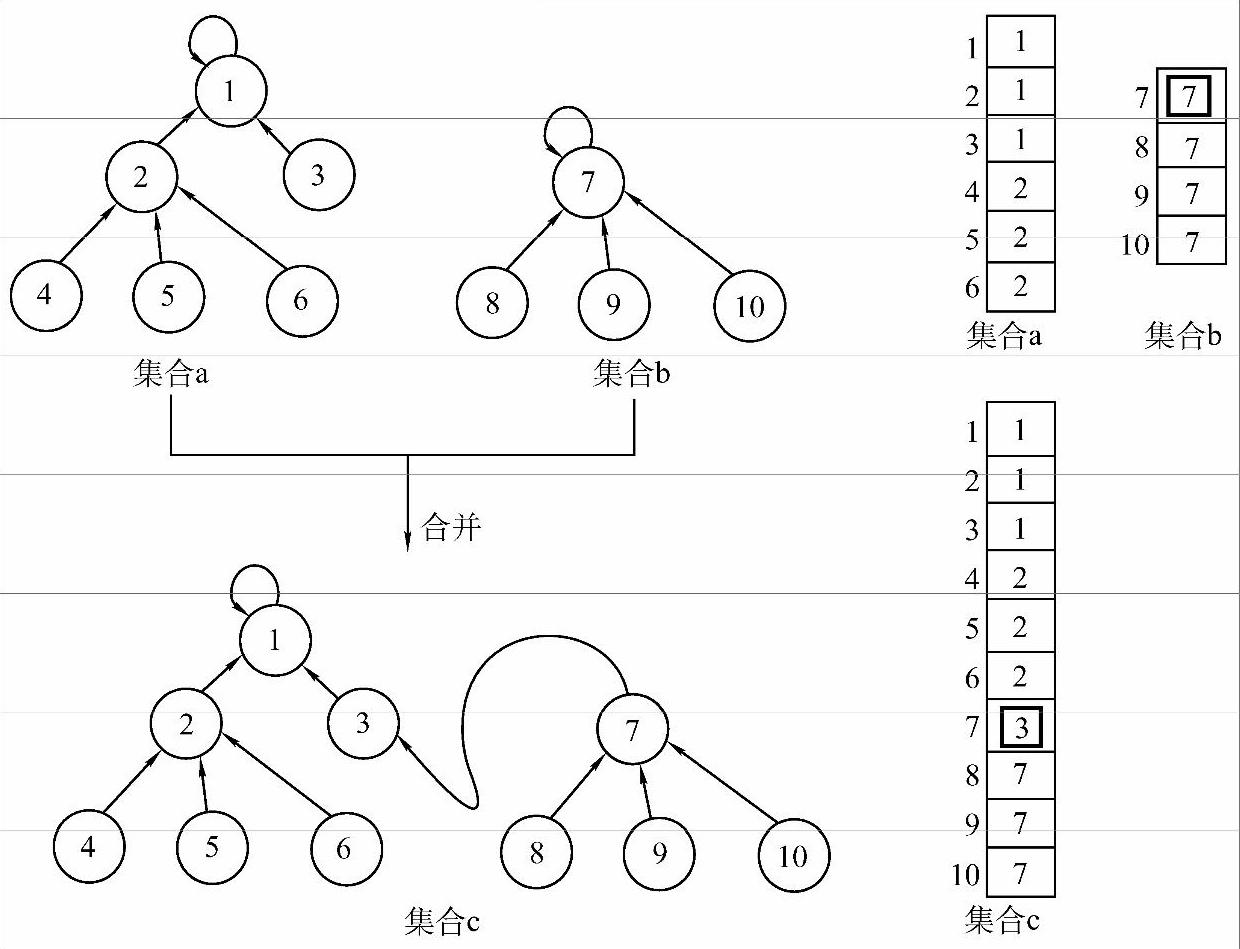
图7-13 并查集在数组中的表示及合并过程

假设road[]数组中已经存放了图中各边及其所连接的两个顶点的信息，且排序函数已经存在，克鲁斯卡尔算法代码如下：

说明：上述克鲁斯卡尔算法中的函数sort（），在考试中要根据题目对算法时间复杂度的要求选择合适的排序函数写出。本节中讲到的两个算法是考研中的重点，要将算法思想、算法执行过程和程序代码在理解的基础上牢记。

（3）克鲁斯卡尔算法时间复杂度分析

从上述克鲁斯卡尔算法代码中可以看出，算法时间花费在函数sort（）和单层循环上。循环是线性级的，可以认为算法时间主要花费在函数sort（）上。因为排序算法时间复杂度一般都大于常量级，因此，克鲁斯卡尔算法的时间复杂度主要由选取的排序算法决定。排序算法所处理数据的规模由图的边数e决定，与顶点数无关，因此克鲁斯卡尔算法适用于稀疏图。

注意：普里姆算法和克鲁斯卡尔算法都是针对于无向图的。