1.图

图由结点的有穷集合V和边的集合E组成。为了与树形结构进行区别，在图结构中常常将结点称为顶点，边是顶点的有序偶对。若两个顶点之间存在一条边，则表示这两个顶点具有相邻关系。

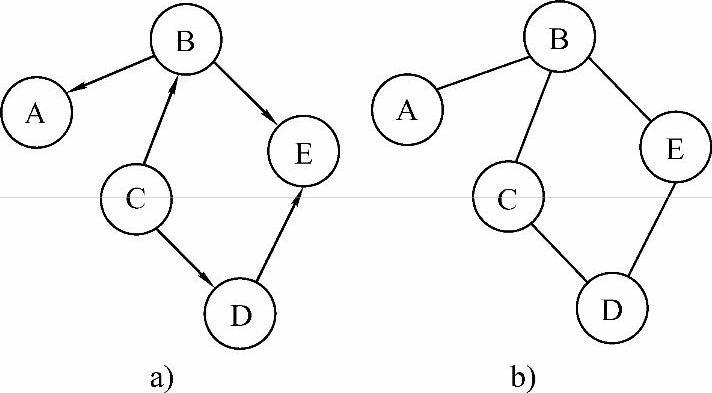
图7-1 有向图和无向图

a）有向图 b）无向图

2.有向图和无向图

在图7-1中，图7-1a是有向图，即每条边都有方向；图7-1b是无向图，即每条边都没有方向。

3.弧

在有向图中，通常将边称为弧，含箭头的一端称为弧头，另一端称为弧尾，记作＜v_i，v_j＞，它表示从顶点v_i到顶点v_j有一条边。

说明：本书中将弧和边统一称为边。

4.顶点的度、入度和出度

在无向图中，边记为（v_i，v_j），它等价于在有向图中存在＜v_i，v_j＞和＜v_j，vi＞两条边。与顶点v相关的边的条数称为顶点v的度。如在图7-1b中，顶点D的度为2。在有向图中，指向顶点v的边的条数称为顶点v的入度，由顶点v发出的边的条数称为顶点v的出度。如在图7-1a中，顶点C的入度为0、出度为2，顶点D的入度为1、出度为1。

5.有向完全图和无向完全图

若有向图中有n个顶点，则最多有n（n-1）条边（图中任意两个顶点都有两条边相连），将具有n（n-1）条边的有向图称为有向完全图。若无向图中有n个顶点，则最多有n（n-1）/2条边（任意两个顶点之间都有一条边），将具有n（n-1）/2条边的无向图称为无向完全图。

6.路径和路径长度

在一个图中，路径为相邻顶点序偶所构成的序列。路径长度是指路径上边的数目。例如，在图7-1a中，＜C，B＞、＜B，A＞是一条路径，长度为2；在图7-1b中，（D，C）、（C，B）、（B，A）是一条路径，长度为3。

7.简单路径

序列中顶点不重复出现的路径称为简单路径。

8.回路

若一条路径中第一个顶点和最后一个顶点相同，则这条路径是一条回路。

9.连通、连通图和连通分量(www.daowen.com)

在无向图中，如果从顶点v_i到顶点v_j有路径，则称v_i和v_j连通。如果图中任意两个顶点之间都连通，则称该图为连通图；否则，图中的极大连通子图称为连通分量。如在图7-2中，图7-2c是一个非连通图，它由图7-2a和图7-2b组成，图7-2a和图7-2b都是连通图。对于图7-2c、图7-2a和图7-2b就是它的两个连通分量。

10.强连通图和强连通分量

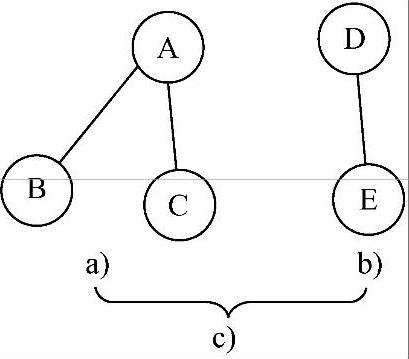
图7-2 非连通图

a）连通图1 b）连通图2

c）组成非连通图

在有向图中，若从v_i到v_j有路径，则称从v_i到v_j是连通的。如果对于每一对顶点v_i和v_j，从v_i到v_j和从v_j到v_i都有路径，则称该图为强连通图；否则，将其中的极大强连通子图称为强连通分量。

11.权和网

图中每条边都可以附有一个对应的数，这种与边相关的数称为权。权可以表示从一个顶点到另一个顶点的距离或者花费的代价。边上带有权的图称为带权图，也称为网。

说明：本书将网和图统称为图。

微信答疑

提问：

极大连通子图中的“极大”两字的确切含义是什么？例如，极小连通子图中的“极小”表示添加一条边就会有环，那么“极大”又是什么意思呢？

回答：

极大连通子图中的“极大”，通俗地理解即不能再大，下面以图7-3为例进行说明。

在图7-3中，A—B是一个连通子图，但不是极大连通子图，因为它还可以再扩充一个顶点C。同理，D—E—F是一个连通子图，但也不是极大连通子图，因为它还可以再扩充一个顶点G。因此，A—B—C和D—E—F—G这两个子图才是极大连通子图，它们都无法再扩充顶点。

综上所述，一个图中的极大连通子图可以这样得到：从一个顶点开始作为一个子图，逐个添加和这个子图有边相连的顶点，直到所有相连的顶点都被纳入图中，所生成的子图就是一个极大连通子图。

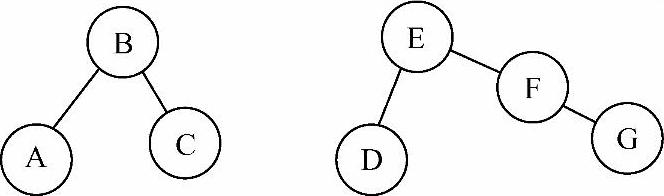
图7-3 极大连通子图