说明：在下面要讲的1～4点内容中，默认赫夫曼树为二叉树。

1.与赫夫曼树相关的一些概念

赫夫曼树又叫作最优二叉树，它的特点是带权路径最短。首先需要说明几个关于路径的概念。

1）路径：路径是指从树中一个结点到另一个结点的分支所构成的路线。

2）路径长度：路径长度是指路径上的分支数目。

3）树的路径长度：树的路径长度是指从根到每个结点的路径长度之和。

4）带权路径长度：结点具有权值，从该结点到根之间的路径长度乘以结点的权值，就是该结点的带权路径长度。

5）树的带权路径长度（WPL）：树的带权路径长度是指树中所有叶子结点的带权路径长度之和。

本节重点是要理解最后三个概念，下面通过一个例子来说明它们。假设图6-28所示二叉树的4个叶子结点a、b、c、d的权值分别为7、5、2、4。因为a到根结点的分支数目为2，所以a的路径长度为2，a的带权路径长度为7×2=14。同样，b、c、d的带权路径长度分别为5×2=10、3×2=6、4×2=8。于是这棵二叉树的带权路径长度为WPL=14+10+6+8=38。

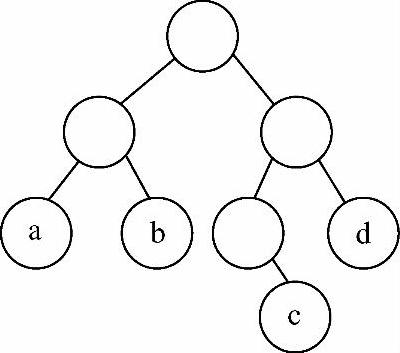
图6-28 有4个叶子结点的二叉树

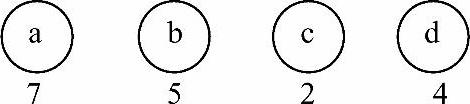
图6-29 带有权值的结点

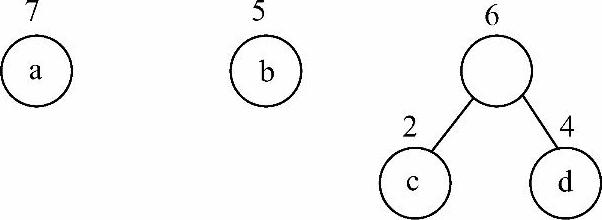
图6-30 将结点c、d构成二叉树

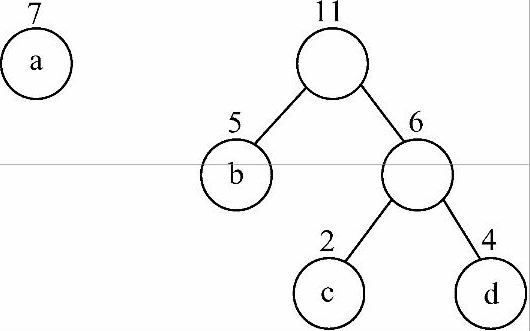
图6-31 将结点b加进去

2.赫夫曼树的构造方法

给定n个权值，用这n个权值来构造赫夫曼树的算法描述如下：

1）将这n个权值分别看作只有根结点的n棵二叉树，这些二叉树构成的集合记为F。

2）从F中选出两棵根结点的权值最小的树（假设为a、b）作为左、右子树，构造一棵新的二叉树（假设为c），新的二叉树的根结点的权值为左、右子树根结点权值之和。

3）从F中删除a、b，加入新构造的树c。

4）重复进行2）、3）两步，直到F中只剩下一棵树为止，这棵树就是赫夫曼树。

下面通过一个例子来说明赫夫曼树的构造过程，如图6-29所示，图中结点下方的数字代表该结点的权值，用图中各结点构造一棵赫夫曼树。

构造步骤如下：

1）先将a、b、c、d看作只有根的4棵二叉树。

2）选出权值最小的两个根c和d，将它们作为左、右子树，构造一棵新的二叉树。新的二叉树的根结点权值为c和d权值之和，删除c和d，同时将新构造的二叉树加入集合中，结果如图6-30所示。

3）继续选择权值最小的两个根，即权值为5和6的两个根结点，将它们作为左、右子树，构造一棵新的二叉树，新的二叉树的根结点权值为5+6=11。删除根权值为5和6的两棵树，同时将新构造的二叉树加入集合中，结果如图6-31所示。

4）继续选择权值最小的两个根，即权值为7和11的两个根，将它们作为左、右子树，构造一棵新的二叉树，新的二叉树的根结点权值为7+11=18。删除根权值为7和11的两棵树，同时将新构造的二叉树加入集合中，最终结果如图6-32所示。

5）此时，集合中只剩下一棵二叉树，这棵二叉树就是赫夫曼树，至此赫夫曼树的构造结束。计算其WPL=7×1+5×2+2×3+4×3=35。在以a、b、c、d这4个结点为叶子结点的所有二叉树中，赫夫曼树的WPL是最小的。

3.赫夫曼树的特点

1）权值越大的结点，距离根结点越近。

2）树中没有度为1的结点。这类树又叫作正则（严格）二叉树。

3）树的带权路径长度最短。

4.赫夫曼编码

前边关于赫夫曼树的讲解中，提到了很多次“最”这个字，如最优二叉树、最短带权路径长度等。“最”可以理解为在一群事物中独特的存在，具有一些突出的特性。能不能利用赫夫曼树最的特性做一些事情呢？如在存储文件的时候，对于包含同一内容的文件有多种存储方式，是不是可以找出一种最节省空间的存储方式？答案是肯定的，这就是赫夫曼编码的用途。常见的.zip压缩文件和.jpeg图片文件的底层技术都用到了赫夫曼编码。(www.daowen.com)

这里用一个简单的例子来说明赫夫曼编码是如何实现对文件进行压缩存储的。如这样一串字符“S=AAABBACCCDEEA”，选三位长度的二进制为各个字符编码（二进制数位数随意，只要够编码所有不同的字符即可），编码规则见表6-2。

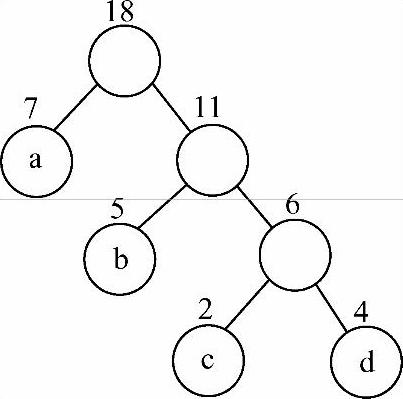
图6-32 最终形成的二叉树

表6-2 三位二进制数对A～E的编码规则

根据表6-2我们可以把S串编码为：

T（S）=000000000001001000010010010011100100000

并将其存储在计算机中，用的时候就可以按照表6-2所示的编码规则，对每三位一个字符进行解码得到S串。

T（S）长度为39，有没有办法使得这个编码串变短一些，且能准确地解码得到原字符串？我们用赫夫曼编码方法来试试。首先统计一下各个字符在字符串中出现的次数，见表6-3。

以字符为根结点，以对应的出现次数为权值，构造一棵赫夫曼树，如图6-33所示。

对图6-23中赫夫曼树每个结点的左右分支进行编号，左0右1，则从根到每个结点的路径上的数字序列即为每个字符的编码，见表6-4所示。

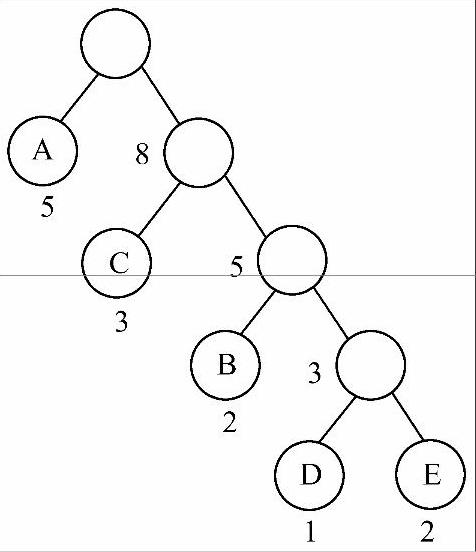
图6-33 赫夫曼树

表6-3 字符在字符串中出现的次数统计

表6-4 对A～E的赫夫曼编码规则

则S串的编码为：

H（S）=00011011001010101110111111110

上述由赫夫曼树导出每个字符的编码，进而得到对整个字符串的编码的过程称为赫夫曼编码。H（S）串长度为29，比T（S）串短了很多。如果原字符串很长，这种压缩带来的空间节约就会更加明显。

这里有同学会提问，前边对S串的编码方式是采取定长码，每三位代表一个字符，解码的时候只要每三位解码一次就可以解码出原字符串；而现在这种编码方式是不定长的，不同的字符可能出现不同长度的编码串，这样如果出现一个字符的编码串是另一个字符编码串的前缀，岂不是会出现解码的歧义？假如A的编码串是0，B的编码串是00，对于00这个编码串，是应该解码为AA还是B呢？这个问题可以用前缀码来解决。在前缀码中，任一字符的编码串都不是另一字符编码串的前缀（这里是以被编码的对象是字符为例）。用前缀码编码，在解码时就不会出现歧义了，观察图6-34，由赫夫曼编码规则产生的恰好是前缀码，如H（S）即是一串前缀码。因为被编码的字符都处于叶子结点上，而根通往任一叶子结点的路径都不可能是通往其余叶子结点路径的子路径，因此任一编码串不可能是其他编码串的子串。

对H（S）解码需要用到图6-34中的那棵赫夫曼树，以H（S）串为指示，一次次沿着根结点走向叶子结点并读出字符的过程即是解码过程。如H（S）串第一个字符为0，从根开始沿着0方向走来到叶子结点，解码出A；回到根，重复上述过程，解码出后边两个A；此时遇到1，从根沿着1方向走，遇到的不是叶子结点，继续读H（S）串，下一个字符是1，继续沿着1走，仍然不是叶子结点，继续读H（S）串，下一个字符是0，则沿着0方向走来到叶子结点，读出B，回到根结点。如此进行下去，直到将所有字符解码出来。

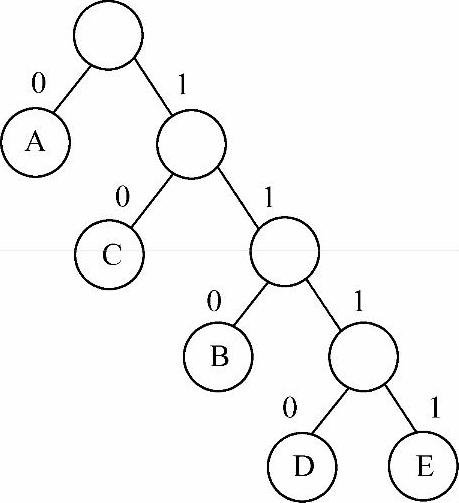
图6-34 赫夫曼编码

到这里，可能有同学又要问了：“我随便画一棵二叉树，同样可以构造出前缀码，为什么非要用赫夫曼树？”由赫夫曼树的特性可知，其树的带权路径长度是最短的。赫夫曼编码过程中，每个字符的权值是在字符串中出现的次数，路径长度即为每个字符编码的长度，出现次数越多的字符编码长度越短，因此就使得其整个字符串被编码后的前缀码长度最短。这里就引了出另一个重要结论，赫夫曼编码产生的是最短前缀码。

注意：对于同一组结点，构造出的赫夫曼树可能不是唯一的。例如，a、b、c、d这4个结点的权值分别为3、2、2、2，先选取权值最小的结点时，有两种可能的选择，即先以b、c构造一棵树或者先以c、d构造一棵树，这样就会产生两棵不同的赫夫曼树，同样也会产生不同的前缀码，同样在考研答卷时也会出现不同的答案。但是对于同一组结点，只要按照赫夫曼树以及前缀码的构造规则，得到的赫夫曼树WPL都是相同的，得到的前缀码长度都是最短的，写出的答案也都是正确的。

说明：即便是题目给出的一组权值都是互不相同的，且构造过程中产生的二叉树根权值也是互不相同的，照样能构造出不同的赫夫曼树和前缀码。例如，只需调换一下左右子树的位置即可产生满足要求的不同结果。虽然这些结果在实际应用中都是等价的，但据笔者调查，几乎所有考研题目中出现的赫夫曼树构造结果都是左子树根权值小于右子树根权值，两子树根权值相同则较矮的子树在左边。难道这是考研出题者的一种“潜规则”？希望大家做题的时候也按照这个规则来答卷，毕竟两棵都满足答案要求的赫夫曼树在长相上可能差别很大，导致阅卷老师误判的概率也会因此而增高，所以还是选择一个阅卷老师最熟悉的形态结果比较好。

5.赫夫曼n叉树

说明：很多参考书上说赫夫曼树就是二叉树，这显然是不对的，因为不论是从赫夫曼树的发明者DavidA.Huffman的论文中，还是在往年考题中，都出现过赫夫曼n叉树（n＞2）。

赫夫曼二叉树是赫夫曼n叉树的一种特例，对于结点数目大于等于2的待处理序列，都可以构造赫夫曼二叉树，但却不一定能构造赫夫曼n叉树。当发现无法构造时，需要补上权值为0的结点让整个序列凑成可以构造赫夫曼n叉树的序列。如序列A（1）、B（3）、C（4）、D（6）（括号内为权值），就不能直接构造赫夫曼三叉树，需要补上一个权值为0的结点。此时新结点序列为：H（0）、A（1）、B（3）、C（4）、D（6），这样就可以类比赫夫曼二叉树的构造方法，每次挑选权值最小的三个结点构造一棵三叉树，以此类推，直到所有结点都被并入树中。具体构造方法以及结果如下：

1）选取当前权值较小的三个结点H、A、B构造一棵三叉树T，根结点权值为4。

2）选取结点C、D和上一步的生成树T的根结点，构造一棵三叉树，根结点权值为14，即为结果赫夫曼三叉树，如图6-35所示。

这棵赫夫曼三叉树的WPL=（0×2）+（1+3）×2+（4+6）×1=18。

从这个结果的表达式可以发现，H结点的存在对WPL值没有影响，因此得到的依然是最小WPL，因此这种补结点的做法是可行的。

说明：在考研数据结构中，要根据具体情况来判断题目考查的是赫夫曼二叉树还是多叉树，在题目没有明确指出的情况下，一般按照赫夫曼二叉树来处理。